吉林省长春市绿园区2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 若 是 方程的解,则 的值是( )A、-1 B、1 C、-3 D、32. 把方程 改写成用含 的代数式表示 的形式,正确的是( )A、 B、 C、 D、3. 不等式 的解集在数轴上表示正确的是( )A、
 B、
B、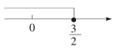 C、
C、 D、
D、 4. 下列选项中的图形,有稳定性的是( )A、
4. 下列选项中的图形,有稳定性的是( )A、 B、
B、 C、
C、 D、
D、 5. 学校购买一种正多边形形状的瓷砖来铺满教室的地面,所购买的瓷砖形状不可能是( )A、等边三角形 B、正五边形 C、正六边形 D、正方形6. 现有两根长度分别 和 的木棒,若要钉成一个三角形木架,则应选取的第三根木棒长可以为( )A、 B、 C、 D、7. 如图, 沿射线 方向平移到 (点E在线段 上),如果 , ,那么平移距离为( )
5. 学校购买一种正多边形形状的瓷砖来铺满教室的地面,所购买的瓷砖形状不可能是( )A、等边三角形 B、正五边形 C、正六边形 D、正方形6. 现有两根长度分别 和 的木棒,若要钉成一个三角形木架,则应选取的第三根木棒长可以为( )A、 B、 C、 D、7. 如图, 沿射线 方向平移到 (点E在线段 上),如果 , ,那么平移距离为( )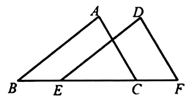 A、3cm B、5cm C、8cm D、13cm8. 如图,将 绕点 顺时针旋转得到 ,且点 恰好在 上, ,则 的度数是( )
A、3cm B、5cm C、8cm D、13cm8. 如图,将 绕点 顺时针旋转得到 ,且点 恰好在 上, ,则 的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
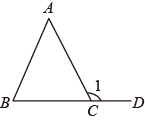
9. 如果 那么 .10. 已知 , 满足方程组 ,则x+y= .11. 若x<y , 试比较大小2x﹣62y﹣6(用“>”、“<”、“=”填空).12. 如图, , ,那么 .
 13. 如图,四边形 ≌四边形 ,则 的大小是 .
13. 如图,四边形 ≌四边形 ,则 的大小是 .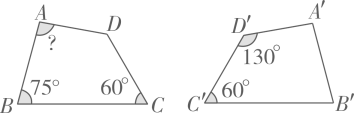 14. 如图,长方形 沿 折叠后,点 、 分别落在点 、 处,若 ,则 的度数为°.
14. 如图,长方形 沿 折叠后,点 、 分别落在点 、 处,若 ,则 的度数为°.
三、解答题
-
15.16. 马小虎在解不等式 的过程中出现了错误,解答过程如下:
解不等式: .
解:去分母,得 .(第一步)
去括号,得 .(第二步)
移项,得 .(第三步)
合并同类项,得 .(第四步)
两边同时除以11,得 .(第五步)
(1)、马小虎的解答过程是从第步开始出现错误的.(2)、请写出此题正确的解答过程.17. 解不等式组: 并在数轴上表示出不等式组的解集 18. 如图,在 的网格中,点 、 、 均为格点(最小正方形的顶点).在图①、图②中分别画一个与 成轴对称的三角形,所画的两个三角形的顶点均在格点上且两个三角形的位置不同.
18. 如图,在 的网格中,点 、 、 均为格点(最小正方形的顶点).在图①、图②中分别画一个与 成轴对称的三角形,所画的两个三角形的顶点均在格点上且两个三角形的位置不同.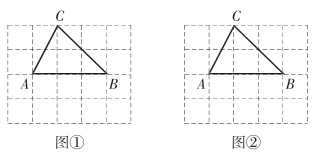 19. 一个多边形的内角和与外角和的度数之和为 ,求这个多边形的边数.20. 如图,将 以点 为旋转中心,顺时针旋转 ,得到 ,过点 作 ,交 的延长线于点 ,求证: .
19. 一个多边形的内角和与外角和的度数之和为 ,求这个多边形的边数.20. 如图,将 以点 为旋转中心,顺时针旋转 ,得到 ,过点 作 ,交 的延长线于点 ,求证: . 21. 某校体育队到体育用品店购买一批篮球和足球,已知买2个篮球和6个足球共需480元;买3个篮球和4个足球共需470元.(1)、求一个篮球和一个足球的售价各是多少元;(2)、结算时,校体育队发现一个篮球商家可以获利25%,则一个篮球的进价是元.22. 先阅读下列解题过程,然后解答问题.
21. 某校体育队到体育用品店购买一批篮球和足球,已知买2个篮球和6个足球共需480元;买3个篮球和4个足球共需470元.(1)、求一个篮球和一个足球的售价各是多少元;(2)、结算时,校体育队发现一个篮球商家可以获利25%,则一个篮球的进价是元.22. 先阅读下列解题过程,然后解答问题.解方程: .
解:当 时,原方程可化为 ,解得 ;
当 时,原方程可化为 ,解得 .
所以原方程的解是 或 .
(1)、解方程: .(2)、已知关于 的方程 .①若方程无解,则 的取值范围是;
②若方程只有一个解,则 的值为;
③若方程有两个解,则 的取值范围是 .
23. (基础知识)(1)、古希腊七贤之一,著名哲学家泰勒斯(Thales , 公元前6世纪)最早从拼图实践中发现了“三角形内角和等于 ”,但这种发现完全是经验性的,泰勒斯并没有给出严格的证明.之后古希腊数学家毕达哥拉斯、欧几里得、普罗科拉斯等相继给出了基于平行线性质的不同的证明.其中欧几里得利用辅助平行线和延长线,通过一组同位角和内错角证明了该定理.请同学们帮助欧几里得将证明过程补充完整.已知:如图,在 中,

求证: .
证明:延长线段 至点 ,并过点 作 .
∵ (已作),
∴ ▲ (两直线平行,内错角相等),
▲ (两直线平行,同位角相等).
∵ ▲ (平角的定义),
∴ (等量代换).
(2)、(实践运用)如图1,线段 、 相交于点 ,连结 、 ,试证明: .证明:
 (3)、(变化拓展)
(3)、(变化拓展)

①如图2, 、 分别平分 、 ,若 , ,则 的度数为 ;
②如图3,直线 平分 , 平分 ,若 , ,则 的度数为 .
24. 如图,在长方形 中, , ,点 从点 出发,沿折线 → → → 运动,到点 停止;点 以每秒 的速度运动6秒,之后以每秒 的速度运动,设点 运动的时间是 (秒),点 运动的路程为 , 的面积是 . (1)、点 共运动秒;(2)、当 时,求 的值;(3)、用含 的代数式表示 ;(4)、当 的面积 是长方形 面积的 时,直接写出 的值
(1)、点 共运动秒;(2)、当 时,求 的值;(3)、用含 的代数式表示 ;(4)、当 的面积 是长方形 面积的 时,直接写出 的值