黑龙江省哈尔滨市南岗区2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 下列方程中,属于二元一次方程的是( )A、 B、 C、 D、2. 下列长度的三条线段可以组成三角形的是( )A、2,3,4 B、4,6,12 C、1,5,9 D、2,5,73. 不等式 的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、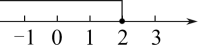 D、
D、 4. 数学老师在课堂上给同学们布置了10个填空题作为课堂练习,并将全班同学的答题情况绘制成条形统计图.由图可知,全班同学答对题数的众数为( )
4. 数学老师在课堂上给同学们布置了10个填空题作为课堂练习,并将全班同学的答题情况绘制成条形统计图.由图可知,全班同学答对题数的众数为( ) A、7 B、8 C、9 D、105. 一个多边形的内角和是它的外角和的2倍,则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形6. 在我县“我的中国梦”演讲比赛中,有7名同学参加了比赛,他们最终决赛的成绩各不相同.其中一名学生想要知道自己是否进入前3名,不仅要知道自己的分数,还得知道这7名学生成绩的( )A、众数 B、方差 C、平均数 D、中位数7. 已知 ,下列式子不一定成立的是( )A、 B、 C、 D、8. 尺规作图作 的平分线方法如下:以 为圆心,任意长为半径画弧交 、 于 、 ,再分别以点 、 为圆心,以大于 长为半径画弧,两弧交于点 ,作射线 由作法得 的根据是( )
A、7 B、8 C、9 D、105. 一个多边形的内角和是它的外角和的2倍,则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形6. 在我县“我的中国梦”演讲比赛中,有7名同学参加了比赛,他们最终决赛的成绩各不相同.其中一名学生想要知道自己是否进入前3名,不仅要知道自己的分数,还得知道这7名学生成绩的( )A、众数 B、方差 C、平均数 D、中位数7. 已知 ,下列式子不一定成立的是( )A、 B、 C、 D、8. 尺规作图作 的平分线方法如下:以 为圆心,任意长为半径画弧交 、 于 、 ,再分别以点 、 为圆心,以大于 长为半径画弧,两弧交于点 ,作射线 由作法得 的根据是( )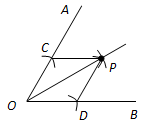 A、SAS B、ASA C、AAS D、SSS9. 若 是关于x和y的二元一次方程ax+y=1的解,则a的值等于( )A、3 B、1 C、﹣1 D、﹣310. 某学校八年级 班九名同学参加定点投篮测试,每人投篮六次,投中的次数统计如下:4,3,5,5,2,5,3,4,1,这组数据的中位数、众数分别为( )A、4,4 B、4,5 C、5,4 D、5,5
A、SAS B、ASA C、AAS D、SSS9. 若 是关于x和y的二元一次方程ax+y=1的解,则a的值等于( )A、3 B、1 C、﹣1 D、﹣310. 某学校八年级 班九名同学参加定点投篮测试,每人投篮六次,投中的次数统计如下:4,3,5,5,2,5,3,4,1,这组数据的中位数、众数分别为( )A、4,4 B、4,5 C、5,4 D、5,5二、填空题
-
11. 把方程3x+y–1=0改写成含x的式子表示y的形式得.12. 不等式组 的解集是 .13. 从甲、乙两人中选拔一人参加职业技能大赛,经过几轮初赛选拔,他们的平均成绩均为 分.方差分别为 , ,你认为适合参加比赛的选手是(填“甲”或“乙”).14. 如图, , 和 是对应边, ,则 度.
 15. 不等式 的最大整数解是16. 某校招聘教师,其中一名教师的笔试成绩是80分,面试成绩是60分,综合成绩笔试占60%,面试占40%,则该教师的综合成绩为分.17. 已知 是 的高, , , 的面积为12,则 .18. 在一次“爱心互助”捐款活动中,某班第一小组8名同学捐款的金额(单位:元)如表所示:
15. 不等式 的最大整数解是16. 某校招聘教师,其中一名教师的笔试成绩是80分,面试成绩是60分,综合成绩笔试占60%,面试占40%,则该教师的综合成绩为分.17. 已知 是 的高, , , 的面积为12,则 .18. 在一次“爱心互助”捐款活动中,某班第一小组8名同学捐款的金额(单位:元)如表所示:金额(元)
5
6
7
10
人数
2
3
2
1
这 名同学捐款的平均金额为元.
19. 课外活动中一些学生分组参加活动,原来每组都为6人,后来重新编组,每组都为8人,这样就比原来减少2组,则这些学生共有人.20. 如图,在 中, ,过点 作 ,且 ,连接 ,若 ,则 的长为 .
三、解答题
-
21. 解下列方程组:(1)、 ;(2)、 .22. 解下列不等式:(1)、 ;(2)、 .23. 如图, 的边 和 的边 在同一条直线上, , .
 (1)、求证: ;(2)、若 ,求证: .24. 某中学全校学生参加了“交通法规”知识竞赛,为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组: ; ; ; ,并绘制出如图不完整的统计图.(图1、图2)
(1)、求证: ;(2)、若 ,求证: .24. 某中学全校学生参加了“交通法规”知识竞赛,为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组: ; ; ; ,并绘制出如图不完整的统计图.(图1、图2) (1)、求被抽取的学生成绩在 组的有 ▲ 人,并把条形统计图补完整;(2)、所抽取学生成绩的中位数落在组内;(3)、若该学校有1500名学生,估计这次竞赛成绩在A组的学生有多少人?25. 某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.在图①中, , ;在图②中, , .图③是该同学所做的一个实验:他将 的直角边 放在 的斜边 上(即点 、E在 上),并将 沿 方向移动.在移动过程中, 、 两点始终在 边上(移动开始时点 与点 重合),在 沿 方向移动的过程中,该同学通过观察和猜想产生以下两个问题,请同学们帮助解答.
(1)、求被抽取的学生成绩在 组的有 ▲ 人,并把条形统计图补完整;(2)、所抽取学生成绩的中位数落在组内;(3)、若该学校有1500名学生,估计这次竞赛成绩在A组的学生有多少人?25. 某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.在图①中, , ;在图②中, , .图③是该同学所做的一个实验:他将 的直角边 放在 的斜边 上(即点 、E在 上),并将 沿 方向移动.在移动过程中, 、 两点始终在 边上(移动开始时点 与点 重合),在 沿 方向移动的过程中,该同学通过观察和猜想产生以下两个问题,请同学们帮助解答. (1)、能否将 移动至某位置,使 、 的连线与 平行?如果能,求出 的度数;(2)、 在移动的过程中, 与 的度数之和是否为定值?若为定值,请求出;若不为定值,请说明理由.26. 某商场准备从供货厂家选购甲、乙两种书包,若购进甲种书包5个和乙种书包4个共需570元;若购进甲种书包6个和乙种书包8个共需940元.(1)、求购进每个甲种、乙种书包的价钱分别为多少元?(2)、若该商场每销售1个甲种书包可获利15元,每销售1个乙种书包可获利20元,且该商场将购进甲、乙两种书包共50个全部售出后,要获得的利润不少于800元,问甲种书包至多购进多少个?27. 已知: 是 的角平分线,且 .
(1)、能否将 移动至某位置,使 、 的连线与 平行?如果能,求出 的度数;(2)、 在移动的过程中, 与 的度数之和是否为定值?若为定值,请求出;若不为定值,请说明理由.26. 某商场准备从供货厂家选购甲、乙两种书包,若购进甲种书包5个和乙种书包4个共需570元;若购进甲种书包6个和乙种书包8个共需940元.(1)、求购进每个甲种、乙种书包的价钱分别为多少元?(2)、若该商场每销售1个甲种书包可获利15元,每销售1个乙种书包可获利20元,且该商场将购进甲、乙两种书包共50个全部售出后,要获得的利润不少于800元,问甲种书包至多购进多少个?27. 已知: 是 的角平分线,且 .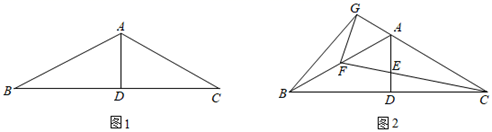 (1)、如图1,求证: ;(2)、如图2, ,点E在 上,连接 并延长交 于点 , 交CA的延长线于点 ,且 ,连接 .
(1)、如图1,求证: ;(2)、如图2, ,点E在 上,连接 并延长交 于点 , 交CA的延长线于点 ,且 ,连接 .①求证: ;
②若 ,且 ,求 的长.