广东省惠州市惠城区2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 如图所示,∠1和∠2是对顶角的是( )A、
 B、
B、 C、
C、 D、
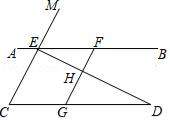
D、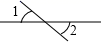 2. 下列点在第三象限的是( )A、(1,1) B、(﹣1,1) C、(﹣1,﹣1) D、(1,﹣1)3. 下列实数: , , , ,0.1010010001…(两个1之间依次增加一个0).无理数的个数有( )A、1个 B、2个 C、3个 D、4个4. 若m>n , 则下列不等式一定成立的是( )A、﹣2m>﹣2n B、 C、m+2>n+2 D、3﹣m>3﹣n5. 下列调查工作需采用普查方式的是( )A、惠州市环保局对西枝江某段水域的水污染情况的调查 B、惠州市电视台对正在播出的某电视节目收视率的调查 C、惠州市质检部门对德赛生产的电池使用寿命的调查 D、2021年6月17号神舟十二号飞船发射前,工作人员对其各个零部件安全情况的检查6. 如图,点E在BC的延长线上,下列四个条件中,不能判断AD BC的是( )
2. 下列点在第三象限的是( )A、(1,1) B、(﹣1,1) C、(﹣1,﹣1) D、(1,﹣1)3. 下列实数: , , , ,0.1010010001…(两个1之间依次增加一个0).无理数的个数有( )A、1个 B、2个 C、3个 D、4个4. 若m>n , 则下列不等式一定成立的是( )A、﹣2m>﹣2n B、 C、m+2>n+2 D、3﹣m>3﹣n5. 下列调查工作需采用普查方式的是( )A、惠州市环保局对西枝江某段水域的水污染情况的调查 B、惠州市电视台对正在播出的某电视节目收视率的调查 C、惠州市质检部门对德赛生产的电池使用寿命的调查 D、2021年6月17号神舟十二号飞船发射前,工作人员对其各个零部件安全情况的检查6. 如图,点E在BC的延长线上,下列四个条件中,不能判断AD BC的是( ) A、∠1=∠2 B、∠D+∠DCB=180° C、∠3=∠4 D、∠D=∠DCE7. 方程组 的解为( )A、 B、 C、 D、8. 如图,直线 的顶点 在 上,若 ,则 ( )
A、∠1=∠2 B、∠D+∠DCB=180° C、∠3=∠4 D、∠D=∠DCE7. 方程组 的解为( )A、 B、 C、 D、8. 如图,直线 的顶点 在 上,若 ,则 ( )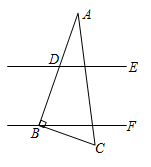 A、 B、 C、 D、9. 已知 是二元一次方程ax+2y=5的一个解,则a的值为( )A、 B、 C、 D、10. 不等式组 的整数解的个数是( )A、2 B、3 C、4 D、5
A、 B、 C、 D、9. 已知 是二元一次方程ax+2y=5的一个解,则a的值为( )A、 B、 C、 D、10. 不等式组 的整数解的个数是( )A、2 B、3 C、4 D、5二、填空题
-
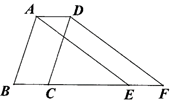
11. 的算术平方根是12. 为了解被拆迁的1680户家庭对拆迁补偿方案是否满意,某主管部门调查了其中的80户家庭,有66户对方案表示满意,14户表示不满意,在这一抽样调查中,样本容量是 .13. 如果点P(m+3,m﹣2)在y轴上,那么m= .14. 如图,将△ABE向右平移3cm得到△DCF,若BE=8cm,则CE=cm.
 15. 在平面直角坐标系中,一个智能机器人接到如下指令,从原点O出发,按向右、向上、向右、向下…的方向依次不断移动,每次移动1个单位,其行走路线如图所示,第1次移动到A1 , 第2次移动到A2 , …第n次移动到An , 则A2021的坐标是 .
15. 在平面直角坐标系中,一个智能机器人接到如下指令,从原点O出发,按向右、向上、向右、向下…的方向依次不断移动,每次移动1个单位,其行走路线如图所示,第1次移动到A1 , 第2次移动到A2 , …第n次移动到An , 则A2021的坐标是 .
三、解答题
-
16. 计算: .17. 解不等式组: ,并将其解集在数轴上表示出来.18. 端午节吃粽子是中华民族的传统习俗.某食品厂为了解市民对去年销量较好的A、B、C、D四种粽子的喜爱情况,在端午节前对某小区居民进行抽样调查(每人只选一种粽子),并将调查情况绘制成如下两幅尚不完整的统计图.
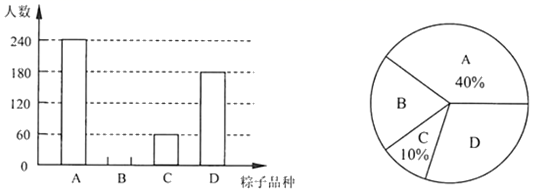
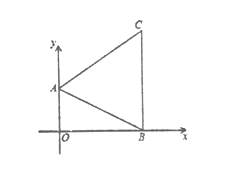
根据以上信息,解答下列问题:
(1)、补全条形统计图;(2)、扇形统计图中,D种粽子所在扇形的圆心角是 ;(3)、这个小区有2500人,请你估计爱吃B种粽子的人数为.19. 如图,网格中的每个小正方形单位长度为1,三角形ABC经过平移后,顶点A平移到了A′(﹣1,4).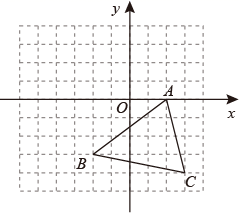 (1)、画出平移后的三角形A′B′C′;(2)、求出三角形ABC的面积.20. “绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买A、B两种型号的垃圾处理设备,已知3台A型设备和2台B型设备日处理能力一共为54吨;5台A型设备和1台B型设备日处理能力一共为62吨.(1)、求1台A型设备、1台B型设备日处理能力各多少吨?(2)、若购买A、B两种型号的垃圾处理设备共20台,并且它们的日处理能力不低于235吨.请你为该景区设计购买A、B两种设备的方案;(3)、已知每台A型设备价格为5万元,每台B型设备价格为7万元.厂家为了促销产品,规定货款不低于137万元时,则按9.5折优惠;问:采用(2)中设计的哪种方案,使购买费用最少,并说明理由.
(1)、画出平移后的三角形A′B′C′;(2)、求出三角形ABC的面积.20. “绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买A、B两种型号的垃圾处理设备,已知3台A型设备和2台B型设备日处理能力一共为54吨;5台A型设备和1台B型设备日处理能力一共为62吨.(1)、求1台A型设备、1台B型设备日处理能力各多少吨?(2)、若购买A、B两种型号的垃圾处理设备共20台,并且它们的日处理能力不低于235吨.请你为该景区设计购买A、B两种设备的方案;(3)、已知每台A型设备价格为5万元,每台B型设备价格为7万元.厂家为了促销产品,规定货款不低于137万元时,则按9.5折优惠;问:采用(2)中设计的哪种方案,使购买费用最少,并说明理由.