云南省保山市2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-19 类型：期末考试

进入出卷网下载

一、单选题

1. 若a的相反数是2 $\sqrt{3}$ ，则a等于（）

A、2 $\sqrt{3}$ B、﹣2 $\sqrt{3}$ C、3 $\sqrt{2}$ D、 $\frac{\sqrt{3}}{6}$

查看试题解析
2. 如图，在△ABC中，CD是角平分线，∠A＝30°，∠CDB＝65°，则∠B的度数为（）

A、65° B、70° C、80° D、85°

查看试题解析
3. 下列二次根式中，最简二次根式的是（）

A、 $\sqrt{\frac{1}{7}}$ B、 $\sqrt{121}$ C、 $\sqrt{48 a}$ D、 $\sqrt{35}$

查看试题解析
4. 下列运算正确的是（）

A、（﹣2a³）²＝4a⁶ B、a²•a⁴＝a⁸ C、a⁶÷a^﹣3＝a³ D、（ $- \frac{1}{3}$ ）^﹣2＝﹣9

查看试题解析
5. 如图，“今有竹高两丈五尺，末折抵地，去本五尺，问折者高几何？”意思是：一根竹子，原来高两丈五尺（一丈为十尺），虫伤有病，一阵风将竹子折断，其竹梢恰好抵地，抵地处离原竹子根部五尺远，则折断处离地面的高度为（）

A、5尺 B、25尺 C、13尺 D、12尺

查看试题解析
6. 一次函数y＝﹣kx﹣2021（k≠0）的函数值y随x的增大而减小，它的图象不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 2021年以来，教育部陆续出台了手机、睡眠、作业、读物、体质等“五项管理”的文件，6月1日发布的《未成年人学校保护规定》也把相关内容纳入其中，将其法治化、制度化．某班人数共有41人，在一次体质测试中，有1人未参加集体测试，老师对集体测试的成绩按40人进行了统计，得到测试成绩分数的平均数是88，中位数是85．缺席集体测试的同学后面进行了补测，成绩为88分，关于该班级41人的体质测试成绩，下列说法正确的是（）

A、平均数不变，中位数变大 B、平均数不变，中位数无法确定 C、平均数变大，中位数变大 D、平均数不变，中位数变小

查看试题解析
8. 如图，正方形ABCD的边长为12，点P是对角线BD上的一个动点，点E在AB上且AE＝7，则△PAE周长的最小值为（）

A、18 B、19 C、20 D、7+12 $\sqrt{2}$

查看试题解析

二、填空题

9. 要使 $\frac{\sqrt{6 - 3 x}}{2}$ 有意义，则x的取值范围为．

查看试题解析
10. 分解因式：5x²y﹣20y＝．

查看试题解析
11. 等腰三角形的两边长分别为3和 $\sqrt{2}$ ，则这个等腰三角形的周长是．

查看试题解析
12. 如图，在四边形ABCD中， $A B // C D$ ， $A D // B C$ ，点E为CD上一点且DE＝3EC ，点F ， G分别是AE ， BE的中点，若FG＝4cm ，则DE的长度为．

查看试题解析
13. 直线y＝kx+b的图象如图所示，则代数式2k﹣b的值为．

查看试题解析
14. 在直角三角形ABC中，若AB＝8，AC﹣BC＝2，则三角形ABC的面积为．

查看试题解析

三、解答题

15. 计算： $- \sqrt{\frac{4}{7}} \times \sqrt{84} -$ （ $\sqrt{3} -$ 2）² ．

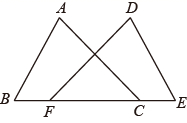
查看试题解析
16. 如图，点C ， F在BE上，BF＝EC ， AB＝DE ， AC＝DF ．
求证：∠A＝∠D ．

查看试题解析
17. 先化简，再求值： $\frac{x y - y^{2}}{x^{2} - y^{2}} - \frac{x^{2} + 2 x y + y^{2}}{x^{2} y + x y^{2}} \div \frac{x + y}{x y}$ ，其中x ， y满足 $\sqrt{x - 1} +$ （y $- \sqrt{2} +$ 1）²＝0．

查看试题解析
18. 如图，在四边形ABCD中，∠A＝90°，AB＝AD＝3 $\sqrt{2}$ ，BC＝10，CD＝8，求四边形ABCD的面积．

查看试题解析
19. 2020年7月至2021年12月，云南省在全省开展以“清垃圾、扫厕所、勤洗手、净餐馆、常消毒、管集市、众参与”为主题的爱国卫生7个专项行动.7个专项行动分别是：裸露垃圾全消除、公共厕所全达标、洗手设施全配套、公共场所清洁消毒全覆盖、餐饮服务环境卫生全改善、农贸市场环境卫生全提升、健康文明生活方式全参与．某社区积极落实7个专项行动要求，计划对社区内的下水道进行升级改造，该工程若由甲工程队单独施工，则恰好在规定时间内完成；若由乙工程队单独施工，则完成的工程所需的天数是规定天数的1.5倍．该工程最后由甲、乙两个工程队先合作施工6天后，再由甲工程队单独施工4天后全部完成，这项工程的规定天数是多少天？

查看试题解析

20. 随机抽取某奶茶店一周的营业额（单位：元）统计如表：

星期	星期一	星期二	星期三	星期四	星期五	星期六	星期日
营业额	700	790	740	740	830	1260	1380

(1)、填空：这一周营业额的平均数是元，中位数是元，众数是元；

(2)、如果要估计该奶茶店一个月（按30天计算）的营业额，你认为（1）中的平均数、中位数、众数中，哪一个最适合用来估计？并用最适合的数据估计该奶茶店一个月的营业额．

查看试题解析

21. 如图，在四边形ABCD中，对角线AC ， BD相交于点O ， OA＝OC ， OB＝OD ，点E是BC延长线上一点，连接DE ， DE $//$ AC ， DE⊥BD ，点D到BE的距离为d ．

(1)、求证：四边形ABCD是菱形；

(2)、若AB＝5，AC＝6，求d ．

查看试题解析

22. 2020年9月8日上午，全国抗击新冠肺炎疫情表彰大会在北京人民大会堂隆重举行．习近平向国家勋章和国家荣誉称号获得者颁授勋章奖章并发表重要讲话．在讲话中，习近平就伟大抗疫精神进行了深刻阐述．他说，在这场同严重疫情的殊死较量中，中国人民和中华民族以敢于斗争、敢于胜利的大无畏气概，铸就了生命至上、举国同心、舍生忘死、尊重科学、命运与共的伟大抗疫精神．为了尽快复工复产，满足疫后市场需求，某公司计划启用大、小车间共8个，并在一周内生产出两种包装的同种商品共计50万件，预计每个大车间每周能生产7万件该商品，每个小车间每周能生产5万件该商品，该公司计划安排4个车间进行A包装，其余进行B包装，已知每个车间每周分别生产两种包装商品的平均成本如表：

车间包装	A包装平均成本（万元/万件）	B包装平均成本（万元/万件）
大车间	5	3
小车间	3	2

(1)、该公司应安排大车间、小车间各多少个，恰好能完成生产任务？

(2)、设进行A包装的大车间有x个，8个车间生产的两种包装商品的总成本为y万元，求y与x的函数解析式（也称关系式），并直接写出x的取值范围；

(3)、若生产A包装的该商品不少于24万件，一共有几种生产方案？哪种方案的总成本y最小？

查看试题解析

23. 如图，在平行四边形ABCD中，对角线AC和BD相交于点O ，点E在BC延长线上，AE平分∠BAD交CD于点F ，点G为EF的中点，连接BG ， CG ， DG ， △ABE的面积为S ， △BGD的周长为l ．

(1)、求证：DF＝BC；

(2)、若GF＝GC ，试判断△DFG与△BCG是否全等，并说明理由；

(3)、在（2）的条件下，若EC＝2，S＝32，求l ．

查看试题解析