山东省聊城市冠县2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 下列图案中,既是中心对称又是轴对称的图案是( )A、
 B、
B、 C、
C、 D、
D、 2. 不等式x+1≥2x﹣1的解集在数轴上表示为( )A、
2. 不等式x+1≥2x﹣1的解集在数轴上表示为( )A、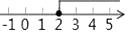 B、
B、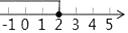 C、
C、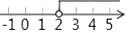 D、
D、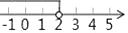 3. 的平方根是( )A、9 B、9和﹣9 C、3 D、3和﹣34. 一条直线y=kx+b,其中k+b<0,kb>0,那么该直线经过( )A、第二、四象限 B、第一、二、三象限 C、第一、三象限 D、第二、三、四象限5. 计算 的结果是( )A、 B、 C、 D、6.
3. 的平方根是( )A、9 B、9和﹣9 C、3 D、3和﹣34. 一条直线y=kx+b,其中k+b<0,kb>0,那么该直线经过( )A、第二、四象限 B、第一、二、三象限 C、第一、三象限 D、第二、三、四象限5. 计算 的结果是( )A、 B、 C、 D、6.如图,▱ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
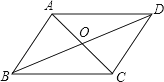 A、10 B、14 C、20 D、227. 如图,用4个相同的直角三角形与一个小正方形拼成的大正方形,若图中直角三角形较短的直角边长是5,小正方形的边长是7,则大正方形的面积是( )
A、10 B、14 C、20 D、227. 如图,用4个相同的直角三角形与一个小正方形拼成的大正方形,若图中直角三角形较短的直角边长是5,小正方形的边长是7,则大正方形的面积是( )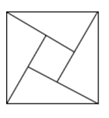 A、121 B、144 C、169 D、1968. 不等式组 的解集是 ,那么m的取值范围( )A、 B、 C、 D、9. 如图,已知一条直线经过点 , ,将这条直线向右平移与 轴, 轴分别交于点 ,若 ,则直线 的函数表达式为( )
A、121 B、144 C、169 D、1968. 不等式组 的解集是 ,那么m的取值范围( )A、 B、 C、 D、9. 如图,已知一条直线经过点 , ,将这条直线向右平移与 轴, 轴分别交于点 ,若 ,则直线 的函数表达式为( ) A、 B、 C、 D、10. 新冠病毒肺炎疫情防控期间,某校为达到开学复课标准,购进一批新桌椅.学校组织100名教师搬桌椅,规定一人一次搬两把椅子,两人一次搬一张桌子,每人限搬一次,最多可搬桌椅(一桌一椅为一套)的套数为( )A、40 B、30 C、20 D、1011. 如图,在平面直角坐标系中,将 绕着旋转中心顺时针旋转 ,得到 ,则旋转中心的坐标为( )
A、 B、 C、 D、10. 新冠病毒肺炎疫情防控期间,某校为达到开学复课标准,购进一批新桌椅.学校组织100名教师搬桌椅,规定一人一次搬两把椅子,两人一次搬一张桌子,每人限搬一次,最多可搬桌椅(一桌一椅为一套)的套数为( )A、40 B、30 C、20 D、1011. 如图,在平面直角坐标系中,将 绕着旋转中心顺时针旋转 ,得到 ,则旋转中心的坐标为( ) A、 B、 C、 D、12. 如图,直线y=﹣x+a与y=x+b的交点的横坐标为﹣2,两直线与x轴交点的横坐标分别是﹣1,﹣3,则关于x的不等式﹣x+a>x+b>0的解集是( )
A、 B、 C、 D、12. 如图,直线y=﹣x+a与y=x+b的交点的横坐标为﹣2,两直线与x轴交点的横坐标分别是﹣1,﹣3,则关于x的不等式﹣x+a>x+b>0的解集是( ) A、x>﹣2 B、x<﹣2 C、﹣3<x<﹣2 D、﹣3<x<﹣1
A、x>﹣2 B、x<﹣2 C、﹣3<x<﹣2 D、﹣3<x<﹣1二、填空题
-
13. 如图所示,数轴上点 所表示的数是 ,化简 的结果为.
 14. 若 是关于 的一元一次不等式,则 .15. 如图, 沿BC方向平移4cm,得到 ,如果四边形ABFD的周长是32cm,则 的周长是cm.
14. 若 是关于 的一元一次不等式,则 .15. 如图, 沿BC方向平移4cm,得到 ,如果四边形ABFD的周长是32cm,则 的周长是cm. 16. 如图,阴影部分是两个正方形,其它部分是两个直角三角形和一个正方形.若右边的直角三角形 中, , ,则阴影部分的面积是 .
16. 如图,阴影部分是两个正方形,其它部分是两个直角三角形和一个正方形.若右边的直角三角形 中, , ,则阴影部分的面积是 . 17. 正方形A1B1C1O、A2B2C2C1、A3B3C3C2、…,按如图所示的方式放置.点A1、A2、A3、…,和点C1、C2、C3 , …,分别在直线y=kx+b (k>0)和x轴上,已知点B1(1,1),B2(3,2),则点B2021的坐标是.
17. 正方形A1B1C1O、A2B2C2C1、A3B3C3C2、…,按如图所示的方式放置.点A1、A2、A3、…,和点C1、C2、C3 , …,分别在直线y=kx+b (k>0)和x轴上,已知点B1(1,1),B2(3,2),则点B2021的坐标是.
三、解答题
-
18.(1)、解不等式2(x+1)﹣ ,并把它的解集在数轴上表示出来;(2)、解不等式组: .19. 计算.(1)、 ;(2)、 ;(3)、 .20. 如图, 三个顶点的坐标分别是 ,

⑴请画出 向左平移6个单位后得到的 ,并写出 的坐标;
⑵请画出 关于原点对称的 ,并写出点 的坐标;
⑶在x轴上求一点P使 周长最小(保留作图痕迹,不写作法)
21. 如图,一架 长的梯子 斜靠在一竖直墙 上,这时 为 . (1)、求 的长度;(2)、如果梯子底端 沿地面向外移动 到达点 ,那么梯子顶端 下移多少 ?22. 如图,△ABC与△AB′C′关于点A成中心对称,且∠BAC=90°,AB=2,AC=4.连接BC′,B'C .
(1)、求 的长度;(2)、如果梯子底端 沿地面向外移动 到达点 ,那么梯子顶端 下移多少 ?22. 如图,△ABC与△AB′C′关于点A成中心对称,且∠BAC=90°,AB=2,AC=4.连接BC′,B'C . (1)、判定四边形B'CBC′的形状,并说明理由;(2)、求出四边形B'CBC'的面积.23. 如图,直线y=﹣ x+8与x轴、y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,
(1)、判定四边形B'CBC′的形状,并说明理由;(2)、求出四边形B'CBC'的面积.23. 如图,直线y=﹣ x+8与x轴、y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处, (1)、点M的坐标;(2)、求直线AM的解析式.24. 新冠肺炎疫情期间,某口罩厂为生产更多的口罩满足疫情防控需求,决定拨款456万元购进 两种型号的口罩机共30台.两种型号口罩机的单价和工作效率分别如表:
(1)、点M的坐标;(2)、求直线AM的解析式.24. 新冠肺炎疫情期间,某口罩厂为生产更多的口罩满足疫情防控需求,决定拨款456万元购进 两种型号的口罩机共30台.两种型号口罩机的单价和工作效率分别如表:单价/万元
工作效率/(只/ )
种型号
16
4000
种型号
14.8
3000
(1)、求购进 两种型号的口罩生产线各多少台.(2)、现有204万只口罩的生产任务,计划安排新购进的口罩机共15台同时进行生产.若工厂的工人每天工作 ,则至少租用 种型号的口罩机多少台才能在5天内完成任务?25. 如图,在△ABC中,O是AC边上一点,过点O作BC的平行线,交∠BCA的平分线于点E , 交外角∠ACD的平分线于点F . (1)、求证:EO=OF;(2)、连接AE , AF , 当点O沿AC移动时,四边形AECF是否能成为一个矩形?此时,点O在什么位置?说明理由
(1)、求证:EO=OF;(2)、连接AE , AF , 当点O沿AC移动时,四边形AECF是否能成为一个矩形?此时,点O在什么位置?说明理由