山东省德州市临邑县2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一次函数y=-5x+3的图象经过的象限是( )A、一、二、三 B、二、三、四 C、一、二、四 D、一、三、四3. 下列计算正确的是( )A、 B、 C、 D、4. 四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:① ;② ;③ ;④ ,从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )A、2种 B、3种 C、4种 D、5种5. 使分式 的值等于零的x
2. 一次函数y=-5x+3的图象经过的象限是( )A、一、二、三 B、二、三、四 C、一、二、四 D、一、三、四3. 下列计算正确的是( )A、 B、 C、 D、4. 四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:① ;② ;③ ;④ ,从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )A、2种 B、3种 C、4种 D、5种5. 使分式 的值等于零的x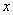 的值是 ( ) A、6 B、-1或6 C、-1 D、-66. 甲乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则下列结论错误的是( ).
的值是 ( ) A、6 B、-1或6 C、-1 D、-66. 甲乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则下列结论错误的是( ).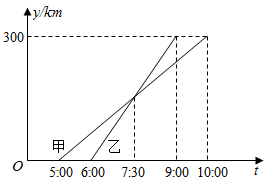 A、甲车的平均速度为 B、乙车的平均速度为 C、乙车比甲车先到 城 D、乙车比甲车先出发7. 一次函数y=-x+6的图象上有两点A(-1, ),B(2, ),则 与 的大小关系是( )A、 > B、 = C、 < D、 ≥8. 甲,乙两班举行电脑汉字输入速度比赛,参赛学生每分钟输入汉字的个数经统计计算后,结果如下. 某同学根据上表分析,得出如下结论.
A、甲车的平均速度为 B、乙车的平均速度为 C、乙车比甲车先到 城 D、乙车比甲车先出发7. 一次函数y=-x+6的图象上有两点A(-1, ),B(2, ),则 与 的大小关系是( )A、 > B、 = C、 < D、 ≥8. 甲,乙两班举行电脑汉字输入速度比赛,参赛学生每分钟输入汉字的个数经统计计算后,结果如下. 某同学根据上表分析,得出如下结论.班级
参加人数
中位数
方差
平均数
甲
55
149
191
135
乙
55
151
110
135
⑴甲,乙两班学生成绩的平均水平相同.⑵乙班优秀的人数多于甲班优秀的人数.(每分钟输入汉字≧150个为优秀.)⑶甲班成绩的波动情况比乙班成绩的波动小.上述结论中正确的是( )
A、(1)(2)(3) B、(1)(2) C、(1)(3) D、(2)(3)9. 某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元, 如果平均每月增长率为x,则由题意列方程应为( )
A、200(1+x)2=1000 B、200+200×2x=1000 C、200+200×3x=1000 D、200[1+(1+x)+(1+x)2]=100010. 如图所示,圆柱的高AB=3,底面直径BC=3,现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是( )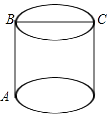 A、 B、 C、 D、11. 如图,正方形 的边长为4,点E在 上且 ,F为对角线 上一动点,则 周长的最小值为( ).
A、 B、 C、 D、11. 如图,正方形 的边长为4,点E在 上且 ,F为对角线 上一动点,则 周长的最小值为( ).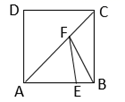 A、5 B、6 C、7 D、812. 如图,在平面直角坐标系中,四边形 ,…都是菱形,点 …都在x轴上,点 ,…都在直线 上,且 ,则点 的横坐标是( )
A、5 B、6 C、7 D、812. 如图,在平面直角坐标系中,四边形 ,…都是菱形,点 …都在x轴上,点 ,…都在直线 上,且 ,则点 的横坐标是( )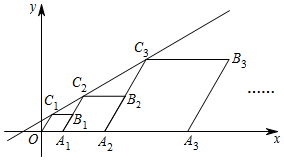 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 函数 中,自变量x的取值范围是 .14. 如图将矩形 沿直线 折叠,顶点D恰好落在 边上F处,已知 ,则 .
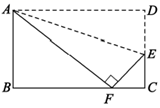 15. 已知一次函数的图象与直线y=﹣x+1平行,且过点(8,2),那么此一次函数的解析式为.16. 菱形 的两条对角线长为方程 的一个根,则菱形 的周长为 .17. 如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=7,则EF的长为 .
15. 已知一次函数的图象与直线y=﹣x+1平行,且过点(8,2),那么此一次函数的解析式为.16. 菱形 的两条对角线长为方程 的一个根,则菱形 的周长为 .17. 如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=7,则EF的长为 .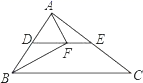 18. 旋转变换在几何证明或计算中有很重要的应用,利用旋转解决问题:如图,P为正方形 内一点, , , ,则 .
18. 旋转变换在几何证明或计算中有很重要的应用,利用旋转解决问题:如图,P为正方形 内一点, , , ,则 .
三、解答题
-
19. 州教育局为了解我州八年级学生参加社会实践活动情况,随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据检测了两幅统计图,下面给出了两幅不完整的统计图(如图)
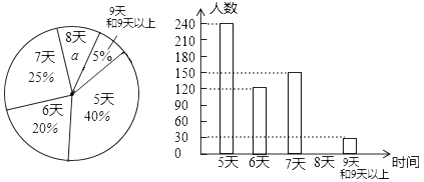
请根据图中提供的信息,回答下列问题:
(1)、a=%,并写出该扇形所对圆心角的度数为 , 请补全条形图 .(2)、在这次抽样调查中,众数和中位数分别是多少?(3)、如果该县共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?
20.(1)、计算:(2)、解方程: .21. 我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:销售单价x(元/件)
…
20
30
40
50
60
…
每天销售量(y件)
…
500
400
300
200
100
…
(1)、把上表中 的各组对应值作为点的坐标,猜想y与x的函数关系,并求出函数关系式;(2)、相关物价部门规定,该工艺品销售单价最高不能超过35元/件,当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润为8000元?22. 如图,在△ABC中 , D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD , 连接BF .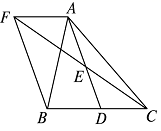 (1)、求证:D是BC的中点(2)、如果AB=AC , 试判断四边形AFBD的形状,并证明你的结论.23. 已知关于x的一元二次方程x2-2kx+ k2-2=0.(1)、求证:不论k为何值,方程总有两不相等实数根.(2)、设x1 , x2是方程的根,且 x12-2kx1+2x1x2=5,求k的值.24. 为了迎接“十•一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
(1)、求证:D是BC的中点(2)、如果AB=AC , 试判断四边形AFBD的形状,并证明你的结论.23. 已知关于x的一元二次方程x2-2kx+ k2-2=0.(1)、求证:不论k为何值,方程总有两不相等实数根.(2)、设x1 , x2是方程的根,且 x12-2kx1+2x1x2=5,求k的值.24. 为了迎接“十•一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:运动鞋
价格
甲
乙
进价(元/双)
m
m﹣20
售价(元/双)
240
160
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)、求m的值;(2)、要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?(3)、在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?25. 如图,在平面直角坐标系中, 为坐标原点,矩形 的顶点 、 ,将矩形 的一个角沿直线 折叠,使得点 落在对角线 上的点 处,折痕与 轴交于点 .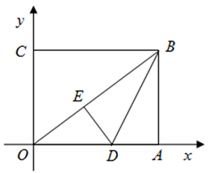 (1)、求线段 的长度;(2)、求直线 所对应的函数表达式;(3)、若点 在线段 上,在线段 上是否存在点 ,使以 为顶点的四边形是平行四边形?若存在,请求出点 的坐标;若不存在,请说明理由.
(1)、求线段 的长度;(2)、求直线 所对应的函数表达式;(3)、若点 在线段 上,在线段 上是否存在点 ,使以 为顶点的四边形是平行四边形?若存在,请求出点 的坐标;若不存在,请说明理由.