江西省九江市2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-19 类型：期末考试

进入出卷网下载

一、单选题

1. 区环卫科正开展“垃圾分类”知识宣传活动，下列图标（不包含文字）是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 分式 $\frac{2}{x - 1}$ 有意义，则x的取值范围是（）

A、x ≠ 1； B、x＞1； C、x＜1； D、x ≠－1

查看试题解析
3. 已知a＜b ，下列式子不成立的是（）

A、a+1＜b+1 B、3a＜3b C、﹣2a＞﹣2b D、如果c＜0，那么 $\frac{a}{c}$ ＜ $\frac{b}{c}$

查看试题解析
4. 下列各式由左边到右边的变形中，属于分解因式的是( )

A、a（x+y）=ax+ay B、x²﹣4x+4=x（x﹣4）+4 C、10x²﹣5x=5x（2x﹣1） D、x²﹣16+6x=（x+4）（x﹣4）+6x

查看试题解析
5. 如图，在△ABC中，∠A＝90°，AB＝3，AC＝4，∠ABC与∠ACB的平分线交于点O ，过点O作OD⊥AB于点D ，则AD的长为（）

A、 $\sqrt{2}$ B、2 C、 $\sqrt{3}$ D、1

查看试题解析
6. 如图，在△ABC中，AB＝6，AC＝8，BC＝10，△ABD ， △ACE ， △BCF都是等边三角形，下列结论中：①AB⊥AC；②四边形AEFD是平行四边形；③∠DFE＝135°；④S_{四边形AEFD}＝20．正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

7. 用不等式表示“x的7倍减去1大于0”是．

查看试题解析
8. 在平面直角坐标系xOy中，若点B与点 $A (- 2 ， 3)$ 关于点O中心对称，则点B的坐标为．

查看试题解析
9. 一项工程，甲单独做x小时完成，乙单独做y小时完成，则两人一起完成这项工程需要小时．

查看试题解析
10. 将正三角形、正方形、正五边形按如图所示的位置摆放，则 $∠ 1 + ∠ 2 + ∠ 3 =$ ．

查看试题解析
11. 如图，在△ABC中，∠A＝30°，F为AC上一点，FD垂直平分AB ，交AB于点D ，线段DF上点E满足EF＝2DE＝2，连接CE、EB ，若BE＝EC ，则CF的长为．

查看试题解析
12. 如图所示，△ADE是将△ABC绕点A顺时针旋转一定角度α（0°＜α＜90°）得到的，AC与DE相交于点M ，其中∠B＝70°，∠C＝30°，现要使得△ADM为等腰三角形，则旋转角α的度数为．

查看试题解析

三、解答题

13.

(1)、因式分解：x²y﹣9y ．

(2)、化简 $\frac{x^{2} - 4 x}{x^{2} - 8 x + 16}$ ．

查看试题解析
14. 解不等式组 ${\begin{matrix} 3 (x - 1) - 1 > x - 8 \\ \frac{x - 7}{2} + 5 \geq x \end{matrix}$ ，并将解集在数轴上表示出来

查看试题解析
15. 先化简，再求值：（1﹣ $\frac{1}{x - 2}$ ）÷ $\frac{x^{2} - 6 x + 9}{2 x - 4}$ ，其中x的值从2，3，4中选取．

查看试题解析
16. 如图，根据要求画图

⑴把△ABC向右平移5个方格，画出平移的△A₁B₁C₁；

⑵以点B为旋转中心，把△ABC顺时针方向旋转90°，画出旋转后的△A₂BC₂ ．

查看试题解析
17. 如图：正方形网格中每个小方格的边长为1，且点A、B、C均为格点．

(1)、通过计算判断△ABC的形状；

(2)、求AB边上的高．

查看试题解析
18.

(1)、已知a+b＝3，ab＝2，求代数式a³b+2a²b²+ab³的值．

(2)、已知方程组 ${\begin{matrix} 2 x + y = 1 - m \\ x + 2 y = 2 \end{matrix}$ 的解x、y满足x+y＞0，求m的取值范围．

查看试题解析
19. 如图，在平行四边形ABCD中，对角线AC，BD相交于点O，分别过点A，C作 $A E ⊥ B D$ ， $C F ⊥ B D$ ，垂足分别为E，F.AC平分 $∠ D A E$ .

(1)、若 $∠ A O E = 50 °$ ，求 $∠ A C B$ 的度数；

(2)、求证： $A E = C F$ .

查看试题解析
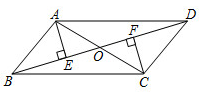20. 现代互联网技术的广泛应用，催生了快递行业的高速发展.小明计划给朋友快递一部分物品，经了解甲、乙两家快递公司比较合适，甲公司表示：快递物品不超过1千克的，按每千克22元收费；超过1千克，超过的部分按每千克15元收费，乙公司表示：按每千克16元收费，另加包装费3元.设小明快递物品x千克.

(1)、当x＞1时，请分别直接写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式；

(2)、在(1)的条件下，小明选择哪家快递公司更省钱？

查看试题解析
21. 如图，在△ABC中，点D为边BC的中点，点E在△ABC内，AE平分∠BAC，CE⊥AE，点F在AB上，且BF=DE．

(1)、求证：四边形BDEF是平行四边形；

(2)、线段AB，BF，AC之间具有怎样的数量关系？证明你所得到的结论．

查看试题解析
22. 某社区拟建 $A$ ， $B$ 两类摊位以搞活“地摊经济”，每个 $A$ 类摊位的占地面积比每个 $B$ 类摊位的占地面积多2平方米，建 $A$ 类摊位每平方米的费用为40元，建 $B$ 类摊位每平方米的费用为30元，用60平方米建 $A$ 类摊位的个数恰好是用同样面积建 $B$ 类摊位个数的 $\frac{3}{5}$ ．

(1)、求每个 $A$ ， $B$ 类摊位占地面积各为多少平方米？

(2)、该社拟建 $A$ ， $B$ 两类摊位共90个，且 $B$ 类摊位的数量不少于 $A$ 类摊位数量的3倍.求建造这90个摊位的最大费用．

查看试题解析
23. 如图

(1)、问题发现：
如图1，点A为线段BC外一动点，且BC＝a ， AB＝b ．填空：当点A位于CB延长线上时，线段AC的长可取得最大值，则最大值为（用含a ， b的式子表示）；

(2)、尝试应用：
如图2所示，△ABC和△ADE均为等腰直角三角形，∠BAC＝∠DAE＝90°，M、N分别为AB、AD的中点，连接MN、CE ． AD＝5，AC＝3．

①请写出MN与CE的数量关系，并说明理由．

②直接写出MN的最大值．

(3)、如图3所示，△ABC为等边三角形，DA＝6，DB＝10，∠ADB＝60°，M、N分别为BC、BD的中点，求MN长．

(4)、若在第（3）中将“∠ADB＝60°”这个条件删除，其他条件不变，请直接写出MN的取值范围．

查看试题解析