吉林省长春市双阳区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 下列式子:a , , , ,其中分式的共有( )A、1个 B、2个 C、3个 D、4个2. 在平面直角坐标系中,点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 数学老师对小明的5次单元测验成绩进行统计分析,要判断小明的数学成绩是否稳定,老师需要知道小明这5次数学成绩的( )A、平均数 B、中位数 C、众数 D、方差4. 如图,在平行四边形ABCD中,若∠A=40°,则∠D的度数为( )
 A、40° B、100° C、140° D、180°5. 如果把 中的x和y都扩大5倍,那么分式的值( )A、扩大5倍 B、不变 C、缩小5倍 D、扩大10倍6. 在平面直角坐标系中,若点A(2,a)和B(2,7)关于x轴对称,则a的值为( )A、2 B、﹣2 C、7 D、﹣77. 计算 的结果是( )A、x B、x2 C、y2 D、y8. 与直线y=﹣4x+2平行的直线是( )A、y=4x+2 B、y=﹣4x+3 C、y D、y9. 对于反比例函数y ,下列说法正确的是( )A、图象经过点(2,1) B、图象位于第一、三象限 C、当x<0时,y随x的增大而减小 D、当x>0时,y随x的增大而增大10. 如图,四边形ABCD为菱形,对角线AC=6,BD=8,且AE垂直于CD , 垂足为点E , 则AE的长度为( )
A、40° B、100° C、140° D、180°5. 如果把 中的x和y都扩大5倍,那么分式的值( )A、扩大5倍 B、不变 C、缩小5倍 D、扩大10倍6. 在平面直角坐标系中,若点A(2,a)和B(2,7)关于x轴对称,则a的值为( )A、2 B、﹣2 C、7 D、﹣77. 计算 的结果是( )A、x B、x2 C、y2 D、y8. 与直线y=﹣4x+2平行的直线是( )A、y=4x+2 B、y=﹣4x+3 C、y D、y9. 对于反比例函数y ,下列说法正确的是( )A、图象经过点(2,1) B、图象位于第一、三象限 C、当x<0时,y随x的增大而减小 D、当x>0时,y随x的增大而增大10. 如图,四边形ABCD为菱形,对角线AC=6,BD=8,且AE垂直于CD , 垂足为点E , 则AE的长度为( )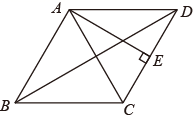 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 使分式 有意义的x的取值范围是 .12. 随着电子制造技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.000 000 7(毫米2),这个数用科学记数法表示为 .13. 计算: .14. 分式 和 的最简公分母是 .15. 当x=时,分式 的值是0.16. 如图,四边形ABCD是正方形,△ABE是等边三角形,则∠AED为 度.
 17. 如图,在平面直角坐标系中,C为y轴正半轴上一点,过点C作直线AB∥x轴,直线分别与反比例函数y 和y 的图象交于A、B两点,连结AO和BO . 若S△AOB=3,则k的值为 .
17. 如图,在平面直角坐标系中,C为y轴正半轴上一点,过点C作直线AB∥x轴,直线分别与反比例函数y 和y 的图象交于A、B两点,连结AO和BO . 若S△AOB=3,则k的值为 .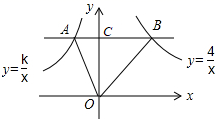 18. 如图,在平行四边形ABCD中,E、F分别是AD、BC边上的点,AF与BE相交于点G , DF与EC相交于点H , 若S△ABG=16,S△DHC=7,则四边形EGFH的面积为 .
18. 如图,在平行四边形ABCD中,E、F分别是AD、BC边上的点,AF与BE相交于点G , DF与EC相交于点H , 若S△ABG=16,S△DHC=7,则四边形EGFH的面积为 .
三、解答题
-
19. 先化简,再求值: ,其中a 1.20. 解方程: .21. 某校八年二班手工制作小组成员小丽、小影两位同学同时为校文化艺术节制作彩旗,已知小丽比小影每小时多做2面彩旗,小丽做40面彩旗与小影做30面彩旗所用时间相等,问小影每小时做多少面彩旗?22. 如图,在5×5的正方形网格中有一条线段AB , 点A、B都在格点上.


 (1)、在图①中以AB为边,画出一个是轴对称,但不是中心对称的四边形ABCD , C、D为格点.(2)、在图②中以AB为边,画出一个是中心对称,但不是轴对称的四边形ABCD , C、D为格点.(3)、在图③中以AB为边,画出一个既是中心对称,又是轴对称的四边形ABCD , C、D为格点.23. 如图,将平行四边形ABCD的边DC延长到点E , 使CE=DC , 连结AE , 交BC于点F , ∠AFC=2∠D , 连结AC、BE . 求证:四边形ABEC是矩形.
(1)、在图①中以AB为边,画出一个是轴对称,但不是中心对称的四边形ABCD , C、D为格点.(2)、在图②中以AB为边,画出一个是中心对称,但不是轴对称的四边形ABCD , C、D为格点.(3)、在图③中以AB为边,画出一个既是中心对称,又是轴对称的四边形ABCD , C、D为格点.23. 如图,将平行四边形ABCD的边DC延长到点E , 使CE=DC , 连结AE , 交BC于点F , ∠AFC=2∠D , 连结AC、BE . 求证:四边形ABEC是矩形.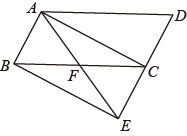 24. “体验劳动乐趣,传承劳动美德”.为了解五一期间学生做家务劳动的时间,某中学对八年级一班50名学生进行了调查,有关数据如表:
24. “体验劳动乐趣,传承劳动美德”.为了解五一期间学生做家务劳动的时间,某中学对八年级一班50名学生进行了调查,有关数据如表:每周做家务的时间(小时)
0
1
1.5
2
2.5
3
3.5
4
人数(人)
1
4
7
8
12
10
6
2
根据如表中的数据,回答下列问题:
(1)、这组数据的中位数是 小时,众数是 小时.(2)、求出该班学生每周做家务劳动的平均时间.(3)、请你根据(1)、(2)的结果,用一句话谈谈自己的感受.25. 如图,直线y=nx+m和双曲线y 相交于点A(2,2)和点B(a , ﹣1). (1)、求k的值;(2)、求n , m的值;(3)、结合图象写出不等式nx+m 的解集: . 注:第(3)小题直接写出结果.26. 甲、乙两车分别从M、N两地同时出发.甲车匀速前往N地,到达N地立即以另一速度按原路匀速返回到M地;乙车匀速前往M地.设甲乙两车与M地之间的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示.
(1)、求k的值;(2)、求n , m的值;(3)、结合图象写出不等式nx+m 的解集: . 注:第(3)小题直接写出结果.26. 甲、乙两车分别从M、N两地同时出发.甲车匀速前往N地,到达N地立即以另一速度按原路匀速返回到M地;乙车匀速前往M地.设甲乙两车与M地之间的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示. (1)、M、N两地之间的路程为 千米,甲车从M地到达N地的行驶时间为 小时.(2)、求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围.(3)、直接写出当甲车与乙车之间的路程为100千米时甲车所用的时间.27. 以下是华师版八年级上册数学教材117页的部分内容.
(1)、M、N两地之间的路程为 千米,甲车从M地到达N地的行驶时间为 小时.(2)、求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围.(3)、直接写出当甲车与乙车之间的路程为100千米时甲车所用的时间.27. 以下是华师版八年级上册数学教材117页的部分内容.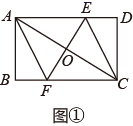
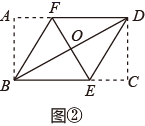
已知:如图,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F , 求证:四边形AFCE是菱形。
(1)、(问题解决)请结合图①写出证明过程.
(2)、(应用拓展)如图②,矩形纸片ABCD , 翻折∠A和∠C , 使AB和CD落在对角线BD上,且点A和点C落在同一点O上,折痕分别是BF和DE , 若四边形BEDF面积为8,则矩形纸片ABCD的面积为 .
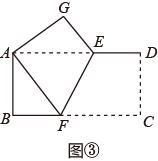
(3)、如图③,矩形纸片ABCD沿着EF折叠,使得点C与点A重合,若AB=4,BC=8,则EF= .28. 在平面直角坐标系中,点O为坐标原点,直线y=x与直线y x+4相交于点A , 直线y x+4与x轴交于点B , 点D为线段OB上的一个动点,点D的横坐标为m , 过点D作DE垂直于x轴,交折线OA﹣AB于点E , 以E为边向右作正方形DEFG .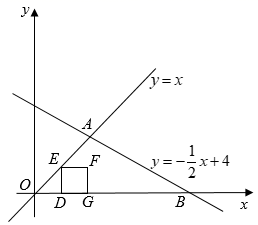 (1)、写出点A的横坐标;(2)、求DE的长(用含m的代数式表示);(3)、当点F落在直线AB上时,求m的值;(4)、当三角形AOB与正方形DEFG重合部分为四边形时,写出重合部分面积S与m之间的函数关系式;(5)、当直线AB经过正方形DEFG某个边的中点时,直接写出m的取值范围.
(1)、写出点A的横坐标;(2)、求DE的长(用含m的代数式表示);(3)、当点F落在直线AB上时,求m的值;(4)、当三角形AOB与正方形DEFG重合部分为四边形时,写出重合部分面积S与m之间的函数关系式;(5)、当直线AB经过正方形DEFG某个边的中点时,直接写出m的取值范围.