河北省唐山市玉田县2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,下列各点在第四象限的是( )A、(﹣2,3) B、(2,0) C、(0,﹣3) D、(3,﹣5)2. 如图,在平行四边形ABCD中,∠B+∠D=100°,则∠A等于( )
 A、50° B、100° C、130° D、150°3. 要想了解九年级1000名考生的数学成绩,从中抽取了100名考生的数学成绩进行统计分析,以下说法正确的是( )A、这100名考生是总体的一个样本 B、每位考生的数学成绩是个体 C、1000名考生是总体 D、100名考生是样本的容量4. 若正比例函数 ,当 时, ,则下列各点在该函数图象上的是( )A、 B、 C、 D、5. 如图,为估计池塘两岸边A , B两点间的距离,在池塘的一侧选取点C , 分别取AC , BC的中点D , E , 测得DE=15m,则A , B两点间的距离是( )
A、50° B、100° C、130° D、150°3. 要想了解九年级1000名考生的数学成绩,从中抽取了100名考生的数学成绩进行统计分析,以下说法正确的是( )A、这100名考生是总体的一个样本 B、每位考生的数学成绩是个体 C、1000名考生是总体 D、100名考生是样本的容量4. 若正比例函数 ,当 时, ,则下列各点在该函数图象上的是( )A、 B、 C、 D、5. 如图,为估计池塘两岸边A , B两点间的距离,在池塘的一侧选取点C , 分别取AC , BC的中点D , E , 测得DE=15m,则A , B两点间的距离是( )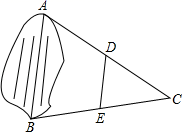 A、15m B、20m C、30m D、60m6. 将某图形的各顶点的横坐标减去3,纵坐标保持不变,可将该图形( )A、横向向右平移3个单位 B、横向向左平移3个单位 C、纵向向上平移3个单位 D、纵向向下平移3个单位7. 如图,菱形ABCD的对角线AC=8,BD=6,则菱形ABCD的周长等于( )
A、15m B、20m C、30m D、60m6. 将某图形的各顶点的横坐标减去3,纵坐标保持不变,可将该图形( )A、横向向右平移3个单位 B、横向向左平移3个单位 C、纵向向上平移3个单位 D、纵向向下平移3个单位7. 如图,菱形ABCD的对角线AC=8,BD=6,则菱形ABCD的周长等于( ) A、14 B、20 C、24 D、288. 下列说法正确的是( )A、若点 ,则点A到x轴的距离为3 B、平行于y轴的直线上所有点的纵坐标都相同 C、 与 表示两个不同的点 D、若点 在x轴上,则9. 下列有关一次函数y=﹣6x﹣5的说法中,正确的是( )A、y的值随着x值的增大而增大 B、函数图象与y轴的交点坐标为(0,5) C、当x>0时,y>﹣5 D、函数图象经过第二、三、四象限10. 下列条件中,能推出▱ABCD为矩形的是( )A、AB=BC B、AC平分∠BAD C、AC⊥BD D、AC=BD11. 小妍从家出发步行上学,途中发现忘带了数学书,于是打电话让妈妈马上从家里沿上学的路送来,同时小妍也掉头往家走,遇到妈妈后聊了一会儿,接着继续向学校走去.设小妍从家出发后所用时间为t , 小妍与学校的距离为s , 下面能反映s与t的函数关系的大致图象是( )A、
A、14 B、20 C、24 D、288. 下列说法正确的是( )A、若点 ,则点A到x轴的距离为3 B、平行于y轴的直线上所有点的纵坐标都相同 C、 与 表示两个不同的点 D、若点 在x轴上,则9. 下列有关一次函数y=﹣6x﹣5的说法中,正确的是( )A、y的值随着x值的增大而增大 B、函数图象与y轴的交点坐标为(0,5) C、当x>0时,y>﹣5 D、函数图象经过第二、三、四象限10. 下列条件中,能推出▱ABCD为矩形的是( )A、AB=BC B、AC平分∠BAD C、AC⊥BD D、AC=BD11. 小妍从家出发步行上学,途中发现忘带了数学书,于是打电话让妈妈马上从家里沿上学的路送来,同时小妍也掉头往家走,遇到妈妈后聊了一会儿,接着继续向学校走去.设小妍从家出发后所用时间为t , 小妍与学校的距离为s , 下面能反映s与t的函数关系的大致图象是( )A、 B、
B、 C、
C、 D、
D、 12. 如图,四边形OABC是正方形,若点B的坐标为(0, ),则点A的坐标是( )
12. 如图,四边形OABC是正方形,若点B的坐标为(0, ),则点A的坐标是( )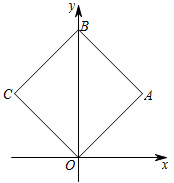 A、 B、 C、(1,1) D、
A、 B、 C、(1,1) D、二、填空题
-
13. 若n边形的每个内角都等于150°,则n= .14. 平面直角坐标系中,点(3,-2)关于x轴对称的点的坐标是 .15. 函数y=2x﹣4的图象与两条坐标轴所围成的三角形的面积是 .16. 如图,在矩形ABCD中,AB=6,对角线AC、BD相交于点O , AE垂直平分BO于点E , 则BD的长为 .
 17. 如图,一次函数 ( )的图象经过点A.当 时,x的取值范围是 .
17. 如图,一次函数 ( )的图象经过点A.当 时,x的取值范围是 .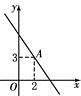 18. 某校抽查部分九年级学生1分钟垫球测试成绩(单位:个),将测试成绩分成4组,得到如图不完整的频数直方图(每一组含前一个边界值,不含后一个边界值),已知在120﹣150组别的人数占抽测总人数的40%,则1分钟垫球少于90个的有人.
18. 某校抽查部分九年级学生1分钟垫球测试成绩(单位:个),将测试成绩分成4组,得到如图不完整的频数直方图(每一组含前一个边界值,不含后一个边界值),已知在120﹣150组别的人数占抽测总人数的40%,则1分钟垫球少于90个的有人. 19. 如图,在菱形ABCD中,∠B=40°,点E在CD上,AE=AC , 则∠BAE=°.
19. 如图,在菱形ABCD中,∠B=40°,点E在CD上,AE=AC , 则∠BAE=°. 20. 甲、乙两人分别从A、B两地出发,相向而行.图中的 , 分别表示甲、乙离B地的距离 与甲出发后所用时间 的函数关系图象,则甲出发小时与乙相遇.
20. 甲、乙两人分别从A、B两地出发,相向而行.图中的 , 分别表示甲、乙离B地的距离 与甲出发后所用时间 的函数关系图象,则甲出发小时与乙相遇.
三、解答题
-
21. 如图,用(﹣1,0)表示A点的位置,用(2,1)表示B点的位置,请你完成下列问题:
 (1)、画出平面直角坐标系;(2)、写出△DEF的三个顶点的坐标;(3)、若以EF为对角线作一个平行四边形DEMF , 请直接写出第四个顶点M的坐标.22. 某校为了解九年级女生“仰卧起坐”成绩的情况,随机选取该年级部分女生进行测试.根据测试成绩绘制统计图表的一部分.
(1)、画出平面直角坐标系;(2)、写出△DEF的三个顶点的坐标;(3)、若以EF为对角线作一个平行四边形DEMF , 请直接写出第四个顶点M的坐标.22. 某校为了解九年级女生“仰卧起坐”成绩的情况,随机选取该年级部分女生进行测试.根据测试成绩绘制统计图表的一部分.成绩等级
频数(人)
频率
优秀
良好
20
0.4
及格
不及格
5

根据以上信息,解答下列问题.
(1)、被测试女生的总人数为 人,成绩等级为“不及格”的女生人数占被测试女生总人数的百分比为 %.(2)、若该校九年级共有240名女生,根据调查结果,估计该校八年级女生成绩等级为“优秀”的学生人数.23. 如图,一次函数y=2x+b的图像与x轴交于点A(2,0),与y轴交于点B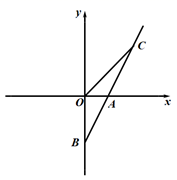 (1)、求b的值(2)、若直线AB上的点C在第一象限,且S△AOC=4,求点C坐标24. 如图,菱形ABCD的对角线AC、BD交于点O , BE∥AC , AE∥BD , 连接EO .
(1)、求b的值(2)、若直线AB上的点C在第一象限,且S△AOC=4,求点C坐标24. 如图,菱形ABCD的对角线AC、BD交于点O , BE∥AC , AE∥BD , 连接EO .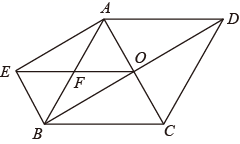 (1)、试判断四边形AEBO的形状,并说明理由;(2)、若CD=6,求OE的长.25. 从地面到高空,气温随离地面高度的变化而变化,当到达一定高度后,气温几乎不再变化.如图是气温 (℃)与离地面高度 ( )之间函数的图象.根据图象解答下列问题:
(1)、试判断四边形AEBO的形状,并说明理由;(2)、若CD=6,求OE的长.25. 从地面到高空,气温随离地面高度的变化而变化,当到达一定高度后,气温几乎不再变化.如图是气温 (℃)与离地面高度 ( )之间函数的图象.根据图象解答下列问题: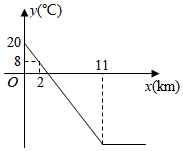 (1)、求地面的气温.(2)、当 时,求 与 之间的函数关系式.(3)、若离地面不同高度的两处气温差为3℃,直接写出这两处中较低处离地面高度 ( )的取值范围.26. “地摊经济”成为社会关注的热门话题,小明从市场得知如下信息:
(1)、求地面的气温.(2)、当 时,求 与 之间的函数关系式.(3)、若离地面不同高度的两处气温差为3℃,直接写出这两处中较低处离地面高度 ( )的取值范围.26. “地摊经济”成为社会关注的热门话题,小明从市场得知如下信息:甲商品
乙商品
进价(元/件)
65
5
售价(元/件)
90
10
小明计划购进甲、乙商品共100件进行销售,设小明购进甲商品x件,甲、乙商品全部销售完后获得利润为y元.
(1)、求出y与x之间的函数关系式.(2)、小明用不超过3500元资金一次性购进甲、乙两种商品,求x的取值范围.(3)、在(2)的条件下,若要求甲,乙商品全部销售完后获得的利润不少于1450元,请说明小明有哪些可行的进货方案,并计算哪种进货方案的利润最大,最大利润是多少?