河北省唐山市滦南县2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 下列调查中,适合采用普查方式的是( )A、防疫期间对进入校园人员进行体温检测 B、了解某市全体学生的体育达标情况 C、了解一批圆珠笔的使用寿命 D、了解我市人民乘坐高铁出行的意愿2. 点A(﹣1,2)到x轴的距离是( )A、﹣1 B、1 C、﹣2 D、23. 下列哪组条件能判别四边形ABCD是平行四边形( )
 A、AB CD , AD=BC B、AB=CD , AD=BC C、∠A=∠B , ∠C=∠D D、AB=AD , CB=CD4. 嘉琪在做“抛一枚正六面体骰子”的实验时,他连续抛了10次,其中“6”点向上共出现3次,则出现“6”点向上的频率是( )A、 B、 C、 D、5. 在国内投寄到外地质量为80g以内的普通信函应付邮资如下表:
A、AB CD , AD=BC B、AB=CD , AD=BC C、∠A=∠B , ∠C=∠D D、AB=AD , CB=CD4. 嘉琪在做“抛一枚正六面体骰子”的实验时,他连续抛了10次,其中“6”点向上共出现3次,则出现“6”点向上的频率是( )A、 B、 C、 D、5. 在国内投寄到外地质量为80g以内的普通信函应付邮资如下表:信件质量m/g
0<m≤20
20<m≤40
40<m≤60
60<m≤80
邮资y/元
1.20
2.40
3.60
4.80
某同学想寄一封质量为15g的信函给居住在外地的朋友,他应该付的邮资是( )
A、4.80 B、3.60 C、2.40 D、1.206. 如图,将□ABCD的一边BC延长至点E , 若∠A=110°,则∠1等于( )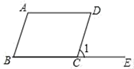 A、110° B、35° C、70° D、55°7. 下列问题中,两个变量之间是正比例函数关系的是( )A、汽车以 的速度匀速行驶,行驶路程 与行驶时间 之间的关系 B、圆的面积 与它的半径 之间的关系 C、某水池有水 ,现打开进水管进水,进水速度 , 后水池有水 D、有一个边长为x的正方体,则它的表面积S与边长x之间的函数关系8. 某校年级有600名学生,从中随机抽取了80名学生进行立定跳远测试.下列说法中:
A、110° B、35° C、70° D、55°7. 下列问题中,两个变量之间是正比例函数关系的是( )A、汽车以 的速度匀速行驶,行驶路程 与行驶时间 之间的关系 B、圆的面积 与它的半径 之间的关系 C、某水池有水 ,现打开进水管进水,进水速度 , 后水池有水 D、有一个边长为x的正方体,则它的表面积S与边长x之间的函数关系8. 某校年级有600名学生,从中随机抽取了80名学生进行立定跳远测试.下列说法中:
这种调查方式是抽样调查;(2)600名学生是总体;(3)这80名学生的立定跳远成绩是总体的一个样本;(4)80名学生是样本容量;(5)每名学生的立定跳远成绩是个体.正确的说法有( )个.A、2 B、3 C、4 D、59. 某个函数自变量的取值范围是 则这个函数的表达式为( )A、 B、 C、 D、10. 若正多边形的一个外角是 ,则这个正多边形的内角和是( )A、540° B、720° C、900° D、1080°11. 如图,在同一直角坐标系中作出一次函数 与 的图象, 则二元一次方程组 的解是( ) A、 B、 C、 D、12. 矩形具有而平行四边形不一定具有的性质是( )A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分13. 已知点(﹣1,y1)、(3,y2)在一次函数y=﹣x+2的图象上,则y1、y2、0的大小关系是( )A、0<y1<y2 B、y1<0<y2 C、y1<y2<0 D、y2<0<y114. 如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )
A、 B、 C、 D、12. 矩形具有而平行四边形不一定具有的性质是( )A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分13. 已知点(﹣1,y1)、(3,y2)在一次函数y=﹣x+2的图象上,则y1、y2、0的大小关系是( )A、0<y1<y2 B、y1<0<y2 C、y1<y2<0 D、y2<0<y114. 如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( ) A、8 B、10 C、12 D、1415. 若点 与点 关于 轴对称,则点 所在象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限16. 如图,小明在操场上匀速散步,某一段时间内先从点M出发到点A,再从点A沿半圆弧到点B,最后从点B回到点M,能近似刻画小明到出发点M的距离与时间之间的关系的图像是( )
A、8 B、10 C、12 D、1415. 若点 与点 关于 轴对称,则点 所在象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限16. 如图,小明在操场上匀速散步,某一段时间内先从点M出发到点A,再从点A沿半圆弧到点B,最后从点B回到点M,能近似刻画小明到出发点M的距离与时间之间的关系的图像是( ) A、
A、 B、
B、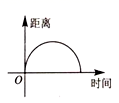 C、
C、 D、
D、
二、填空题
-
17. 小鸡孵化场孵化出一批小鸡,工人在其中50只小鸡上做记号后让这批小鸡充分跑散,后来再任意抓出100只小鸡,其中有记号的有10只,则这批小鸡大约有只。18. 如图,点A,E,F,C在一条直线上,若将△DEC的边EC沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于点E,BF⊥AC于点F,且AB=CD.则当点E,F不重合时,BD与EF的关系是 .
 19. 设矩形一组邻边长分别为x , y , 面积S是定值,已知x=2时,矩形的周长为6.则(1)、y关于x的函数解析式是 ;(2)、自变量x的取值范围是 .20. 在平面直角坐标系xOy中,已知四边形ABCD是平行四边形,且点A(0,-2),点B(m,m+1),点C(6,2).(1)、线段AC的中点E的坐标为;(2)、对角线BD长的最小值为 .
19. 设矩形一组邻边长分别为x , y , 面积S是定值,已知x=2时,矩形的周长为6.则(1)、y关于x的函数解析式是 ;(2)、自变量x的取值范围是 .20. 在平面直角坐标系xOy中,已知四边形ABCD是平行四边形,且点A(0,-2),点B(m,m+1),点C(6,2).(1)、线段AC的中点E的坐标为;(2)、对角线BD长的最小值为 .三、解答题
-
21. 已知点P(2x﹣3,3﹣x)到两个坐标轴的距离相等,试确定点P的坐标.22. 去年疫情期间,某学校积极响应教育部“停课不停学”的号召,积极组织本校教师开展线上教学,为了解学生线上教学的学习效果,决定随机抽取八年级部分学生进行质量测评.以下是根据测试的数学成绩绘制的统计表和频数分布直方图:
成绩x/分
频数
频率
第1段
x<60
2
0.04
第2段
60≤x<70
6
0.12
第3段
70≤x<80
9
b
第4段
80≤x<90
a
0.36
第5段
90≤x≤100
15
0.30

请根据所给信息,解答下列问题:
(1)、统计表中a和b的值各是多少?(2)、此次抽样的样本容量是 , 补全频数分布直方图;(3)、样本中,若某同学测试的数学成绩为76分,则这个样本中,测试分数高于76分的至少有 人,至多有 人.23. 暑假期间,舅舅开车带小明去旅游,6时40分出发,9时20分到达景点.小明每隔20min读一次计程器,记录下来,制成如表:时刻
路程/km
时刻
路程/km
时刻
路程/km
6:40
0
7:40
80
8:40
110
7:00
15
8:00
96
9:00
115
7:20
47
8:20
105
9:20
135
(1)、从家到旅游点全程共有多少千米?汽车共行驶了多长时间?(2)、在下面的直角坐标系中,画出行驶过程中路程随时间变化的函数图象; (3)、汽车在6:40~8:00和8:00~9:00这两个时间段内的平均行驶速度各是多少km/小时?24. 一辆中型客车,准乘21人(包括一名司机和一名乘务员).这辆客车由A地,行驶到B地,油费为45元,高速公路费为20元,其它运输成本为42元,乘客票价25元/人.设乘客人数为x人时,客车盈利y元.(1)、写出y与x之间的函数关系式;(2)、至少要有多少名乘客才能保证不亏本?若载满了乘客,可获利多少元?25. 如图
(3)、汽车在6:40~8:00和8:00~9:00这两个时间段内的平均行驶速度各是多少km/小时?24. 一辆中型客车,准乘21人(包括一名司机和一名乘务员).这辆客车由A地,行驶到B地,油费为45元,高速公路费为20元,其它运输成本为42元,乘客票价25元/人.设乘客人数为x人时,客车盈利y元.(1)、写出y与x之间的函数关系式;(2)、至少要有多少名乘客才能保证不亏本?若载满了乘客,可获利多少元?25. 如图
 (1)、如图1,已知ABCD是正方形,P是对角线AC上一点,求证:PB=PD;
(1)、如图1,已知ABCD是正方形,P是对角线AC上一点,求证:PB=PD;请你完成问题情境中(2)的证明
(2)、如图2,在正方形ABCD中,点P是对角线AC上一点,PE⊥AB , PF⊥BC , 垂足分别为E、F , 连接EF , 猜想EF与DP的数量关系,并证明你的猜想.26. 如图所示,点A是平面直角坐标系内一点坐标为(1, ),AB是过点A的一条直线,B是直线与x轴的交点,以OA、OB为邻边作平行四边形AOBC . 若OD是∠AOB的平分线,且D是AC的中点. (1)、求B、D两点的坐标;(2)、求直线AB的解析式;(3)、若P是直线AB上一动点,且S△POD S平行四边形AOBC , 请直接写出满足条件的点P的坐标.
(1)、求B、D两点的坐标;(2)、求直线AB的解析式;(3)、若P是直线AB上一动点,且S△POD S平行四边形AOBC , 请直接写出满足条件的点P的坐标.