河北省保定市高阳县2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 若二次根式 有意义,则下列各数中,实数x不可以取的值是( )A、﹣1 B、0 C、1 D、22. 函数y=﹣2x的图象一定经过点( )A、(2,﹣1) B、( ,1) C、(﹣2,1) D、(﹣1, )3. 下列计算正确的是( )A、 B、 C、 D、4. 下列图象中,y是x的函数的是( )A、
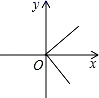 B、
B、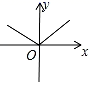 C、
C、 D、
D、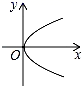 5. 如图,在菱形 中,标出了四条线段的长度,其中有一个长度是标错的,这个长度是( )
5. 如图,在菱形 中,标出了四条线段的长度,其中有一个长度是标错的,这个长度是( )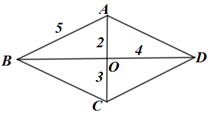 A、2 B、3 C、4 D、56. 放学以后,小红和小颖从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖20分钟到家,小红和小颖家的直线距离为( )A、600米 B、800米 C、1000米 D、不能确定7. 若a= ,b= ,则a与b的关系为( )A、a+b=0 B、ab=1 C、a=b D、无法判断8. 如图,在 中对角线AC,BD相交于点O,点E,F分别是AB,AO的中点,连接EF,若EF=2,则BD的长为(...)
A、2 B、3 C、4 D、56. 放学以后,小红和小颖从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖20分钟到家,小红和小颖家的直线距离为( )A、600米 B、800米 C、1000米 D、不能确定7. 若a= ,b= ,则a与b的关系为( )A、a+b=0 B、ab=1 C、a=b D、无法判断8. 如图,在 中对角线AC,BD相交于点O,点E,F分别是AB,AO的中点,连接EF,若EF=2,则BD的长为(...) A、10 B、8 C、6 D、49. 已知两条线段的长分别为 cm、 cm,那么能与它们组成直角三角形的第三条线段是( )A、1cm或 cm B、1cm C、 cm D、5cm10. 在平面直角坐标系中,将函数 的图象向上平移6个单位长度,则平移后的图象与x轴的交点坐标为( )A、(2,0) B、(-2,0) C、(6,0) D、(-6,0)11. 在对一组样本数据进行分析时,小华列出了方差的计算公式 ,由公式提供的信息,则下列说法错误的是( )A、样本的容量是4 B、样本的中位数是3 C、样本的众数是3 D、样本的平均数是3.512. 如图,已知一次函数y=kx+b的图象经过点A(5,0)与B(0,﹣4),那么关于x的不等式kx+b<0的解集是( )
A、10 B、8 C、6 D、49. 已知两条线段的长分别为 cm、 cm,那么能与它们组成直角三角形的第三条线段是( )A、1cm或 cm B、1cm C、 cm D、5cm10. 在平面直角坐标系中,将函数 的图象向上平移6个单位长度,则平移后的图象与x轴的交点坐标为( )A、(2,0) B、(-2,0) C、(6,0) D、(-6,0)11. 在对一组样本数据进行分析时,小华列出了方差的计算公式 ,由公式提供的信息,则下列说法错误的是( )A、样本的容量是4 B、样本的中位数是3 C、样本的众数是3 D、样本的平均数是3.512. 如图,已知一次函数y=kx+b的图象经过点A(5,0)与B(0,﹣4),那么关于x的不等式kx+b<0的解集是( )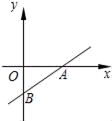 A、x<5 B、x>5 C、x<﹣4 D、x>﹣413. 计算( +1)2020•( ﹣1)2021的结果为( )A、 B、 C、1 D、314. 下表列出了某校田径队成员的年龄分布情况:
A、x<5 B、x>5 C、x<﹣4 D、x>﹣413. 计算( +1)2020•( ﹣1)2021的结果为( )A、 B、 C、1 D、314. 下表列出了某校田径队成员的年龄分布情况:年龄/岁
13
14
15
16
频数
6
18
n
12﹣n
则对于不同的n , 下列关于年龄的统计量一定不发生改变的是( )
A、众数、中位数 B、中位数、方差 C、平均数、中位数 D、平均数、众数15. 如图:用一张长为4cm,宽3cm的长方形纸片,过两个顶点剪一个三角形,按裁剪线长度所标的数据(单位:cm)不可能实现的是( )A、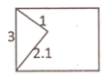 B、
B、 C、
C、 D、
D、 16. 如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位;天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )
16. 如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位;天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( ) A、第24天的销售量为200件 B、第10天销售一件产品的利润是15元 C、第12天与第30天这两天的日销售利润相等 D、第30天的日销售利润是750元
A、第24天的销售量为200件 B、第10天销售一件产品的利润是15元 C、第12天与第30天这两天的日销售利润相等 D、第30天的日销售利润是750元二、填空题
-
17. 如果x1与x2的平均数是4,那么x1+1与x2+5的平均数是 .18. 若二次根式 与 的和是一个二次根式,则正整数a的最小值为 .19. 定义:如图,若菱形AECF与正方形ABCD两个顶点A,C重合,另外两个顶点E,F在正方形ABCD的内部,则称菱形AECF为正方形ABCD的内含菱形.
若正方形的周长为16,其内含菱形边长是整数,则内含菱形的周长为;
若正方形的面积为18,其内含菱形的面积为6,则内含菱形的边长为 .

三、解答题
-
20. 计算:(1)、 .(2)、 .21. 如图,在▱ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE.求证:四边形BEDF是矩形.
 22. 如图,每个小正方形的边长都是1.A、B、C、D均在网格的格点上.
22. 如图,每个小正方形的边长都是1.A、B、C、D均在网格的格点上. (1)、求边BC、BD的长度.(2)、∠BCD是直角吗?请证明你的判断.(3)、找到格点E , 画出四边形ABED , 使其面积与四边形ABCD面积相等(一个即可,且E与C不重合).23. 本学期开学初,学校体育组对八年级某班50名学生进行了跳绳项目的测试,根据测试成绩绘制了下面两幅统计图,根据统计图解答下列问题:
(1)、求边BC、BD的长度.(2)、∠BCD是直角吗?请证明你的判断.(3)、找到格点E , 画出四边形ABED , 使其面积与四边形ABCD面积相等(一个即可,且E与C不重合).23. 本学期开学初,学校体育组对八年级某班50名学生进行了跳绳项目的测试,根据测试成绩绘制了下面两幅统计图,根据统计图解答下列问题: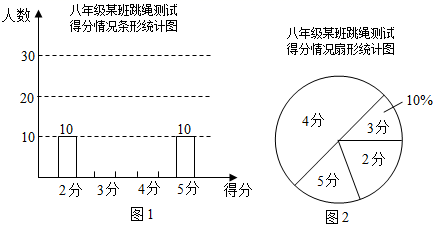 (1)、补全条形统计图;(2)、求本次测试成绩的中位数为 , 众数为;(3)、通过一段时间的训练,体育组对该班50名学生的跳绳项目进行了第二次测试,测试成绩的最低分为3分,且得4分和5分的人数共有45人,中位数没变,众数变为5,求得5分的人数有多少?24. 如图,在直角坐标系中,一次函数的图象l1与y轴交于点A(0,2),与一次函数y=x﹣3的图像l2交于点E(m , ﹣5).
(1)、补全条形统计图;(2)、求本次测试成绩的中位数为 , 众数为;(3)、通过一段时间的训练,体育组对该班50名学生的跳绳项目进行了第二次测试,测试成绩的最低分为3分,且得4分和5分的人数共有45人,中位数没变,众数变为5,求得5分的人数有多少?24. 如图,在直角坐标系中,一次函数的图象l1与y轴交于点A(0,2),与一次函数y=x﹣3的图像l2交于点E(m , ﹣5). (1)、求m的值及l1的表达式.(2)、直线l1与x轴交于点B , 直线l2与y轴交于点C , 求四边形OBEC的面积.(3)、如图,已知矩形MNPQ , PQ=2,NP=1,M(a , 1),矩形MNPQ的边PQ在x轴上平移,若矩形MNPQ与直线l1或l2有交点,直接写出a的取值范围.25. 如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE过点E作EG⊥DE , 使EG=DE,连接FG , FC .
(1)、求m的值及l1的表达式.(2)、直线l1与x轴交于点B , 直线l2与y轴交于点C , 求四边形OBEC的面积.(3)、如图,已知矩形MNPQ , PQ=2,NP=1,M(a , 1),矩形MNPQ的边PQ在x轴上平移,若矩形MNPQ与直线l1或l2有交点,直接写出a的取值范围.25. 如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE过点E作EG⊥DE , 使EG=DE,连接FG , FC . (1)、请判断:FG与CE的数量关系是 , 位置关系是 .(2)、如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请写出判断并予以证明;(3)、如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?如果成立,直接写出结论;如果不成立,说明理由.26. 某农业合作社计划投资200万元,开展甲、乙两项种植项目。已知两个项目的收益(万元)均与投资金额(万元)成正比例,但比例系数不同,设投资甲项目的资金为x(万元),两个项目的总收益为y(万元),且在经营过程中,获得的部分数据如下:
(1)、请判断:FG与CE的数量关系是 , 位置关系是 .(2)、如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请写出判断并予以证明;(3)、如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?如果成立,直接写出结论;如果不成立,说明理由.26. 某农业合作社计划投资200万元,开展甲、乙两项种植项目。已知两个项目的收益(万元)均与投资金额(万元)成正比例,但比例系数不同,设投资甲项目的资金为x(万元),两个项目的总收益为y(万元),且在经营过程中,获得的部分数据如下:x(万元)
10
120
y(万元)
79
68
(1)、求y与x的函数关系式;(2)、嘉淇说:“两个项目的总收益可以是50万元”,你同意他的说法吗?说明你的理由;(3)、若投资甲项目的收益不低于投资乙项目的收益的 ,求y的最大值.