广东省肇庆市高要区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 要使二次根式 有意义,x必须满足( )A、x≤2 B、x≥2 C、x<2 D、x>22. 一组数据2,3,4,6,6,7的众数是( )A、3 B、4 C、5 D、63. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、4. 若函数 是正比例函数,且 随 的增大而减小,则下列判断正确的是( )A、 B、 C、 D、5. 下列各组数中,能够作为直角三角形的三边长的一组是( )A、1,2,3 B、2,3,4 C、4,5,6 D、3,4,56. 如图,将▱ABCD的一边BC延长至点E , 若∠A=110°,则∠1等于( )
 A、70° B、65° C、60° D、55°7. 若b>0,则一次函数y=﹣x+b的图象大致是( )A、
A、70° B、65° C、60° D、55°7. 若b>0,则一次函数y=﹣x+b的图象大致是( )A、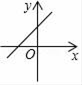 B、
B、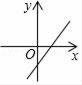 C、
C、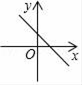 D、
D、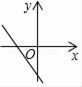 8. 某校九年级体育模拟测试中,六名男生引体向上的成绩如下(单位:个):10、6、9、11、8、10,下列关于这组数据描述正确的是( )A、中位数是9 B、中位数是9.5 C、中位数是10 D、中位数是9和109. 在△ABC中,已知AB=1,BC=1,AC= ,则( )A、∠A=90° B、∠B=90° C、∠C=90° D、∠A=60°10. 如图,在平面直角坐标系中,菱形ABCD的边长为6,它的一边AB在 轴上,且AB的中点是坐标原点,点D在 轴正半轴上,则点C的坐标为( )
8. 某校九年级体育模拟测试中,六名男生引体向上的成绩如下(单位:个):10、6、9、11、8、10,下列关于这组数据描述正确的是( )A、中位数是9 B、中位数是9.5 C、中位数是10 D、中位数是9和109. 在△ABC中,已知AB=1,BC=1,AC= ,则( )A、∠A=90° B、∠B=90° C、∠C=90° D、∠A=60°10. 如图,在平面直角坐标系中,菱形ABCD的边长为6,它的一边AB在 轴上,且AB的中点是坐标原点,点D在 轴正半轴上,则点C的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: = .12. 甲、乙、丙、丁四位同学参加体育训练,近期10次跳绳测试的平均成绩都是每分钟174个,其方差如下表:
选手
甲
乙
丙
丁
方差
0.023
0.018
0.020
0.021
则这10次跳绳中,这四个人发挥最稳定的是 同学.
13. 已知关于x的一次函数y=kx+4的图象经过点(1,2),则k的值是 .14. 若正比例函数y=(m﹣2)x的图象经过点A(x1 , y1)和点B(x2 , y2),当x1<x2时y1>y2 , 则m的取值范围是 .15. 如图,在菱形ABCD中,对角线BD=4,AC=3BD , 则菱形ABCD的面积为 . 16. 如图,一木杆在离地面1.5m处折断,木杆顶端落在离木杆底端 处,则木杆折断之前的高(m).
16. 如图,一木杆在离地面1.5m处折断,木杆顶端落在离木杆底端 处,则木杆折断之前的高(m). 17. 如图,矩形 的两条对角线相交于点 , , ,则矩形的面积等于 .
17. 如图,矩形 的两条对角线相交于点 , , ,则矩形的面积等于 .
三、解答题
-
18. 计算: ﹣(π﹣ )0﹣19. 如图,正方形网格的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上.
 (1)、分别求出AB,BC,AC的长;(2)、试判断△ABC是什么三角形,并说明理由.20. 已知平行四边形ABCD,对角线AC、BD交于点O,线段EF过点O交AD于点E,交BC于点F.求证:OE=OF.
(1)、分别求出AB,BC,AC的长;(2)、试判断△ABC是什么三角形,并说明理由.20. 已知平行四边形ABCD,对角线AC、BD交于点O,线段EF过点O交AD于点E,交BC于点F.求证:OE=OF.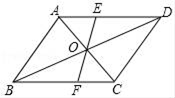 21. 已知一次函数的图象经过点(2,1)和(0,-2).(1)、求该函数的解析式;(2)、判断点(-4,6)是否在该函数图象上.22. 甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
21. 已知一次函数的图象经过点(2,1)和(0,-2).(1)、求该函数的解析式;(2)、判断点(-4,6)是否在该函数图象上.22. 甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表. (1)、在图1中,“7分”所在扇形的圆心角等于 .(2)、请你将图2的条形统计图补充完整;(3)、经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.23. 如图所示,在△ABC中,CD⊥AB于D,AC=4,BC=3,CD=
(1)、在图1中,“7分”所在扇形的圆心角等于 .(2)、请你将图2的条形统计图补充完整;(3)、经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.23. 如图所示,在△ABC中,CD⊥AB于D,AC=4,BC=3,CD= (1)、求AD的长;(2)、求证:△ABC是直角三角形.24. 现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.(1)、请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;(2)、小明选择哪家快递公司更省钱?25. 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)、求AD的长;(2)、求证:△ABC是直角三角形.24. 现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.(1)、请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;(2)、小明选择哪家快递公司更省钱?25. 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.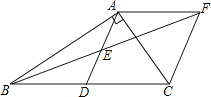 (1)、求证:△AEF≌△DEB
(1)、求证:△AEF≌△DEB
(2)、证明四边形ADCF是菱形。
(3)、若AC=4,AB=5,求菱形ADCF的面积.