安徽省芜湖市南陵县2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-19 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图案是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在函数y＝ $\sqrt{2 - x}$ 中，自变量x的取值范围是（）

A、x＞2 B、x≠2 C、x＜2 D、x≤2

查看试题解析
3. 下列不能判定四边形ABCD是平行四边形的条件是（）

A、AB∥CD，AD∥BC B、OA＝OC，OB＝OD C、AB∥CD，AD＝BC D、AB＝CD，AD＝BC

查看试题解析
4. 已知一次函数y＝kx－1，若y随x的增大而增大，则它的图象经过（）

A、第一、二、三象限 B、第一、二、四象限 C、第一、三、四象限 D、第二、三、四象限

查看试题解析
5. 正方形具有而矩形不具有的性质是（）

A、对角相等 B、对角线互相平分 C、对角线相等 D、对角线互相垂直

查看试题解析
6. 某校有25名同学参加比赛，预赛成绩各不相同，要取前12名参加决赛，小颖已经知道了自己的成绩，她想知道自己能否进入决赛，只需再知道这25名同学成绩的（）

A、中位数 B、众数 C、平均数 D、方差

查看试题解析
7. 在如图4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M₁N₁P₁ ，则其旋转中心可能是（）

A、点A B、点B C、点C D、点D

查看试题解析
8. 如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F，若BF=12，AB=10，则AE的长为（）

A、13 B、14 C、15 D、16

查看试题解析
9. 如图，设甲、乙两车在同一直线公路上匀速行驶，开始甲车在乙车的前面，当乙车追上甲车后，两车停下来，把乙车的货物转给甲车，然后甲车继续前行，乙车原地返回．设x小时后两车间的距离为y千米，y关于x的函数关系如图所示，则乙车的速度为（）

A、50千米/小时 B、45千米/小时 C、40千米/小时 D、35千米/小时

查看试题解析
10. 如图，已知菱形 $A B C D$ 的边长为6，点 $M$ 是对角线 $A C$ 上的一动点，且 $∠ A B C = 120 °$ ，则 $M A + M B + M D$ 的最小值是（）

A、 $3 \sqrt{3}$ B、 $3 + 3 \sqrt{3}$ C、 $6 + \sqrt{3}$ D、 $6 \sqrt{3}$

查看试题解析

二、填空题

11. 分解因式：mn²﹣m= ．

查看试题解析

12. 下表记录了甲、乙、丙、丁四名同学最近五次数学考试成绩的平均分与方差：

	甲	乙	丙	丁
平均分	93	96	96	93
方差 $(s^{2})$	5.1	5.1	1.2	1.2

要选择一名成绩好且发挥稳定的同学参加数学比赛，应该选择．

查看试题解析

13. 若 $4^{a} = 2 ， 4^{b} = 5 ，$ 则 $4^{a - b} =$ ．

查看试题解析
14. 如图，直线 $y = k x + b$ 经过点 $A (m ， - 2)$ 和点 $B (- 2 ， 0)$ ，直线 $y = 2 x$ 过点A，则不等式 $2 x > k x + b$ 的解集为.

查看试题解析
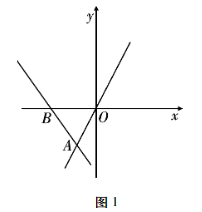15. 在△ABC中，∠BAC=90°，AB=AC=4，O是BC的中点，D是腰AB上一点，把△DOB沿OD折叠得到△DOB′，当∠ADB′=45°时，BD的长度为．

查看试题解析

三、解答题

16. 计算： $\sqrt{64} + 3 \sqrt{12} \div \sqrt{2} - 2 \sqrt{3} \times 3 \sqrt{2}$ ．

查看试题解析
17. 如图，在□ABCD中，连接BD ，在BD的延长线上取一点E ，在DB的延长线上取一点F ，使BF＝DE ，连接AF、CE ．求证：AF∥CE ．

查看试题解析
18. 观察下面各式的规律：
1²+（1×2）²+2²＝（1×2+1）²；

2²+（2×3）²+3²＝（2×3+1）²；

3²+（3×4）²+4²＝（3×4+1）²；

…

(1)、写出第2021个式子；

(2)、写出第n个式子，并验证你的结论．

查看试题解析
19. 如图，在正方形网格中每个小正方形的边长为1，小正方形的顶点称为格点，在正方形网格中分别画出下列图形：

(1)、在图（1）网格中画出长为 $\sqrt{5}$ 的线段AB．

(2)、在图（2）网格中画出一个腰长为 $\sqrt{10}$ ，面积为3的等腰 $Δ D E F$

查看试题解析

20. “新型冠状病毒肺炎”疫情牵动着亿万国人的心，为进一步加强疫情防控工作，某校利用网络平台进行疫情防控知识测试，测试题共10小题，每小题10分.小明同学对八（1）班和八（2）班两个班各40名同学的测试成绩（单位：分）进行了整理和分析，统计数据如下：

①八（1）班成绩频数分布直方图如图：

②八（2）班成绩平均分的计算过程如下：

$\frac{60 \times 3 + 70 \times 17 + 80 \times 3 + 90 \times 9 + 100 \times 8}{40} = 80.5$ （分）；

③数据分析如下：

班级	平均数	中位数	众数	方差
八（1）班	82.5	$m$	90	158.75
八（2）班	80.5	75	$n$	174.75

根据以上信息，解答下列问题：

(1)、

m =

，

n =

；

(2)、你认为班的成绩更加稳定，理由是；

(3)、在本次测试中，八（1）班甲同学和八（2）班乙同学的成绩均为80分，你认为两人在各自班级中谁的成绩排名更靠前?请说明理由.

查看试题解析

21. 今年初，很多商场由于受新型冠状病毒肺炎疫情的影响，产品销售情况不如人意某市甲、乙两家商场利用微信平台进行销售，在平台上购买商品不仅免费送货上门，而且还有优惠其中甲商场所有商品按 $9$ 折出售，乙商场对--次购物中超过 $200$ 元后的价格部分打 $8$ 折．设商品原价为 $x$ 元，实际购物金额为 $y$ 元

(1)、分别就这两家商场的让利方式写出 $y$ 关于 $x$ 的函数解析式；

(2)、当 $x \geq 200$ 时，如何选择这两家商场去购物更省钱？

查看试题解析
22. 在正方形ABCD中，点E是射线AC上一点，点F是正方形ABCD外角平分线CM上一点，且CF=AE，连接BE，EF.

(1)、如图1，当E是线段AC的中点时，直接写出BE与EF的数量关系；

(2)、当点E不是线段AC的中点，其它条件不变时，请你在图2中补全图形，判断(1)中的结论是否成立，并证明你的结论；

(3)、当点B，E，F在一条直线上时，求∠CBE的度数.(直接写出结果即可)

查看试题解析