安徽省十五校联考2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-19 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、2 $\sqrt{5}$ ×3 $\sqrt{5}$ ＝6 $\sqrt{5}$ B、3 $\sqrt{2}$ ×3 $\sqrt{3}$ ＝3 $\sqrt{6}$ C、4 $\sqrt{2}$ ×2 $\sqrt{3}$ ＝8 $\sqrt{5}$ D、2 $\sqrt{2}$ ×6 $\sqrt{3}$ ＝12 $\sqrt{6}$

查看试题解析
2. 如图，△ABC中，点P是AB边上的一点，过点P作PD∥BC，PE∥AC，分别交AC，BC于点D，E，连按CP．若四边形CDPE是菱形，则线段CP应满足的条件是（）

A、CP平分∠ACB B、CP⊥AB C、CP是AB边上的中线 D、CP＝AP

查看试题解析
3. 已知a<b，化简二次根式 $\sqrt{- 8 a^{3} b}$ （）

A、 $2 a \sqrt{- 2 a b}$ B、 $- 2 a \sqrt{2 a b}$ C、 $2 a \sqrt{2 a b}$ D、 $- 2 a \sqrt{- 2 a b}$

查看试题解析
4. 如图，在平行四边形ABCD中，AB=4，BC=6，分别以A ， C为圆心，以大于 $\frac{1}{2}$ AC的长为半径作弧，两弧相交于M ， N两点，作直线MN交AD于点E ，则△CDE的周长是（）

A、7 B、10 C、11 D、12

查看试题解析
5. 已知关于 $x$ 的一元二次方程 $x^{2} - b x - 2 = 0$ ，则下列关于该方程根的判断中正确的是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数 $b$ 的取值有关

查看试题解析
6. 若a，b为方程 $x^{2} - 5 x - 1 = 0$ 的两个实数根，则2 $a^{2} + 3 ab + 8 b - 2 a$ 的值为（）

A、-41 B、-35 C、39 D、45

查看试题解析
7. 如图，□ABCD中，EF∥AB，DE∶DA = 2∶5，EF = 4，则CD的长为（）

A、 $\frac{16}{3}$ B、8 C、10 D、16

查看试题解析
8. 如果关于x的一元二次方程k²x²﹣（2k+1）x+1＝0有两个实数根，那么k的取值范围是（）

A、k≥﹣ $\frac{1}{4}$ B、k≥﹣ $\frac{1}{4}$ 且k≠0 C、k＜﹣ $\frac{1}{4}$ D、k＞－ $\frac{1}{4}$ 且k≠0

查看试题解析
9. 关于 $x$ 的一元二次方程 $x^{2} + 2 m x + 2 n = 0$ 有两个整数根且乘积为正，关于 $y$ 的一元二次方程 $y^{2} + 2 n y + 2 m = 0$ 同样也有两个整数根且乘积为正，给出三个结论：①这两个方程的根都负根；② ${(m - 1)}^{2} + {(n - 1)}^{2} \geq 2$ ；③ $- 1 \leq 2 m - 2 n \leq 1$ ，其中正确结论的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
10. 如图，正方形ABCD中，E为BC的中点，CG⊥DE于G，BG延长交CD于点F，CG延长交BD于点H，交AB于N.下列结论：①DE=CN；② $\frac{B H}{D H} = \frac{1}{2}$ ；③S_△_DEC=3S_△_BNH；④∠BGN=45°；⑤ $G N + E G = \sqrt{2} B G$ .其中正确结论的个数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 最简二次根式 $\sqrt[a - b]{3 a}$ 和 $\sqrt{2 a - b + 2}$ 是同类二次根式，则a＝， b＝．

查看试题解析
12. 方程 $\frac{1}{x + 2} + \frac{4}{x^{2} - 4} = 1$ 的解是．

查看试题解析
13. 如图， $R t △ A B C$ 中， $A B = 9 ， B C = 6 ， ∠ B = 90 °$ ，将 $△ A B C$ 折叠，使 $A$ 点与 $B C$ 的中点 $D$ 重合，折痕为 $M N ，$ 则线段 $B N$ 的长为.

查看试题解析
14. 已知关于x的方程 $x^{2} - (a + b) x + ab - 1 = 0$ ，x₁、x₂是此方程的两个实数根，现给出三个结论：①x₁≠x₂；②x₁x₂＜ab；③ $x_{1}^{2} + x_{2}^{2} {<a}^{2} + b^{2}$ .则正确结论的序号是.（填上你认为正确结论的所有序号）

查看试题解析

三、解答题

15. 解下列方程：

(1)、 $3 x^{2} - 8 x = 3$

(2)、 ${(2 x - 1)}^{2} = 3 (1 - 2 x)$

查看试题解析
16. 先化简，再求值： $\frac{x^{2} + y^{2} - 2 x y}{x - y} \div (\frac{x}{y} - \frac{y}{x})$ ，其中 $x = \sqrt{2} + 1$ ， $y = \sqrt{2} - 1$ .

查看试题解析
17. 已知关于x的一元二次方程kx²+（2k+1）x+2=0．

(1)、求证：无论k取任何实数时，方程总有实数根；

(2)、若方程的两个根的平方和等于5，求k的值．

查看试题解析
18. 如图，在等腰Rt△ABC中，∠BAC＝90°，延长BA至点D，连结DC，过点B作BE⊥DC于点E，F为BC上一点，FC＝FE.连结AF，AE.

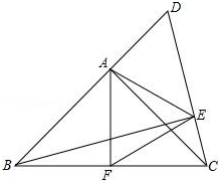(1)、求证：FA＝FE.

(2)、若∠D＝60°，BC＝10，求△AEF的周长.

查看试题解析
19.
如图，E是▱ABCD的边CD的中点，延长AE交BC的延长线于点F．

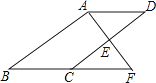(1)、求证：△ADE≌△FCE．

(2)、若∠BAF=90°，BC=5，EF=3，求CD的长．

查看试题解析
20. HW公司2018年使用自主研发生产的“QL”系列甲、乙、丙三类芯片共2800万块，生产了2800万部手机，其中乙类芯片的产量是甲类芯片的2倍，丙类芯片的产量比甲、乙两类芯片产量的和还多400万块.这些“QL”芯片解决了该公司2018年生产的全部手机所需芯片的10%.

(1)、求2018年甲类芯片的产量；

(2)、HW公司计划2020年生产的手机全部使用自主研发的“QL”系列芯片.从2019年起逐年扩大“QL”芯片的产量，2019年、2020年这两年，甲类芯片每年的产量都比前一年增长一个相同的百分数m%，乙类芯片的产量平均每年增长的百分数比m%小1，丙类芯片的产量每年按相同的数量递增.2018年到2020年，丙类芯片三年的总产量达到1.44亿块.这样，2020年的HW公司的手机产量比2018年全年的手机产量多10%，求丙类芯片2020年的产量及m的值.

查看试题解析

21. 近年来，校园安全问题引起了社会的极大关注，为了让学生了解安全知识，增强安全意识，某校举行了一次“安全知识竞赛”．为了了解这次竞赛的成绩（取整数）情况，从中抽取了部分学生的成绩为一个样本，绘制了如下不完整统计图、表（说明：A级：90分﹣100分；B级：75分﹣89分；C级：60分﹣74分；D级：60分以下）．

类别频数

类别	频数（人数）	频率
$A$	49	0.49
$B$	36	0.36
$C$	$m$	0.1
$D$	5	$n$

请结合统计图、表中提供的信息，解答下列问题：

(1)、统计表中m= ，n= ，并把条形统计图补充完整．

(2)、本次竞赛的中位数落在级；

(3)、若该校共有2000名学生，请你用此样本估计安全知识竞赛中A级和B级的学生共有多少人？

查看试题解析

22. 阅读材料：把根式 $\sqrt{x \pm 2 \sqrt{y}}$ 进行化简，若能找到两个数m、n ，是m²+n²＝x且mn＝ $\sqrt{y}$ ，则把x±2 $\sqrt{y}$ 变成m²+n²±2mn＝(m±n)²开方，从而使得 $\sqrt{x \pm 2 \sqrt{y}}$ 化简．
例如：化简 $\sqrt{3 + 2 \sqrt{2}}$

解：∵3+2 $\sqrt{2}$ ＝1+2+2 $\sqrt{2}$ ＝1²+( $\sqrt{2}$ )²+2×1× $\sqrt{2}$ ＝(1+ $\sqrt{2}$ )²

∴ $\sqrt{3 + 2 \sqrt{2}} = \sqrt{{(1 + \sqrt{2})}^{2}} = 1 + \sqrt{2}$ ；

请你仿照上面的方法，化简下列各式：

(1)、 $\sqrt{5 + 2 \sqrt{6}}$ ；

(2)、 $\sqrt{7 - 4 \sqrt{3}}$ .

查看试题解析
23. 如图，点P是边长为4的正方形ABCD的边BC上任意一点，过B点作BG⊥AP于点G ，过C点作CE⊥AP于点E ，连接BE ．

(1)、如图1，若点P是BC的中点，求CE的长；

(2)、如图2，当点P在BC边上运动时（不与B、C重合），求 $\frac{A G － C E}{B E}$ 的值；

(3)、当PB＝时，△BCE是等腰三角形．

查看试题解析