安徽省马鞍山市和县2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 下列计算结果正确的是( )A、 B、 C、 D、2. 如图所示,函数 和 的图像相交于 , 两点,当 时, 的取值范围是( )
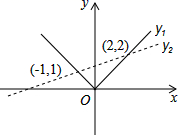 A、 B、 C、 或 D、3. 如图,四边形ABCD是边长为5cm的菱形,其中对角线BD与AC交于点O,BD=6cm,则对角线AC的长度是( )
A、 B、 C、 或 D、3. 如图,四边形ABCD是边长为5cm的菱形,其中对角线BD与AC交于点O,BD=6cm,则对角线AC的长度是( )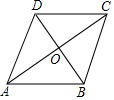 A、8cm B、4cm C、3cm D、6cm4. 下列命题为真命题的是( )A、四个角相等的四边形是矩形 B、对角线互相平分且垂直的四边形是矩形 C、对角线互相平分且相等的四边形是菱形 D、四边相等的四边形是正方形5. 甲、乙两班举行电脑汉字输入比赛,参赛学生每分输入汉字的个数统计结果如下表:
A、8cm B、4cm C、3cm D、6cm4. 下列命题为真命题的是( )A、四个角相等的四边形是矩形 B、对角线互相平分且垂直的四边形是矩形 C、对角线互相平分且相等的四边形是菱形 D、四边相等的四边形是正方形5. 甲、乙两班举行电脑汉字输入比赛,参赛学生每分输入汉字的个数统计结果如下表:班级
参加人数
中位数
方差
平均数
甲
55
149
1.91
135
乙
55
151
1.10
135
某同学分析上表后得到如下结论:
①甲、乙两班学生平均成绩相同;②乙班优秀的人数多于甲班优秀的人数(每分输入汉字个数 为优秀)③甲班成绩的波动比乙班大.
上述结论中正确的是( )
A、①②③ B、①② C、①③ D、②③6. 如图,用两个完全相同的含45°角的直角三角板,不能拼成( ) A、平行四边形 B、正方形 C、等腰三角形 D、有一个内角为45°的菱形7. 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC= ,则折痕CE的长为( )
A、平行四边形 B、正方形 C、等腰三角形 D、有一个内角为45°的菱形7. 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC= ,则折痕CE的长为( )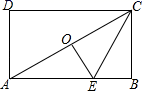 A、2 B、 C、 D、38. 实践证明1分钟跳绳测验的最佳状态是前20秒速度匀速增加,后10秒冲刺,中间速度保持不变,则跳绳速度v(个/秒)与时间t(秒)之间的函数图象大致为( )A、
A、2 B、 C、 D、38. 实践证明1分钟跳绳测验的最佳状态是前20秒速度匀速增加,后10秒冲刺,中间速度保持不变,则跳绳速度v(个/秒)与时间t(秒)之间的函数图象大致为( )A、 B、
B、 C、
C、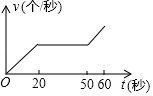 D、
D、 9. 八(1)班班长统计2017年5~12月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制出如下折线统计图,下列说法错误的是( )
9. 八(1)班班长统计2017年5~12月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制出如下折线统计图,下列说法错误的是( ) A、众数是58 B、平均数是50 C、中位数是58 D、每月阅读数量超过40本的有6个月10. 如图,将腰长为4的等腰直角三角形放在直角坐标系中,顺次连接各边中点得到第1个三角形,再顺次连接各边中点得到第2个三角形……,如此操作下去,那么,第6个三角形的直角顶点坐标为( )
A、众数是58 B、平均数是50 C、中位数是58 D、每月阅读数量超过40本的有6个月10. 如图,将腰长为4的等腰直角三角形放在直角坐标系中,顺次连接各边中点得到第1个三角形,再顺次连接各边中点得到第2个三角形……,如此操作下去,那么,第6个三角形的直角顶点坐标为( )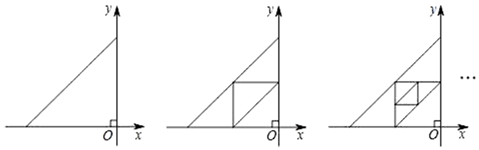 A、(﹣ , ) B、(﹣ , ) C、(﹣ , ) D、(﹣ , )
A、(﹣ , ) B、(﹣ , ) C、(﹣ , ) D、(﹣ , )二、填空题
-
11. 若点D、E分别是 的边AB、AC的中点, ,则BC的长为;12. 一组数据按从小到大排列为1,2,4, ,6,9,这组数据的中位数为5,那么这组数据的众数为 .13. 已知a、b、c是△ABC三边的长,且满足关系式 ,
则△ABC的形状为
14. 如图,已知直线l:y= x , 过点M(2,0)作x轴的垂线交直线l于点N , 过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1 , 过点N1作直线l的垂线交x轴于点M2 , …;按此作法继续下去,则点M3坐标为 .
三、解答题
-
15. 计算: .16. 已知x﹣ ,求x+ 的值.17. 在如图所示的7×7网格中,每个小正方形的边长均为1,点A、B均落在格点上.
 (1)、AB的长等于;(2)、请在如图所示的网格中,用无刻度的直尺,画出一个以AB为边的正方形ABCD,并简要说明画图的方法(不要求证明).18. 如图,已知AB∥DE,AB=DE,AF=DC,求证:四边形BCEF是平行四边形.
(1)、AB的长等于;(2)、请在如图所示的网格中,用无刻度的直尺,画出一个以AB为边的正方形ABCD,并简要说明画图的方法(不要求证明).18. 如图,已知AB∥DE,AB=DE,AF=DC,求证:四边形BCEF是平行四边形. 19. 某学校为选拔数学能力突出的学生参加中学生数学竞赛,组织了多次测试,其中甲乙两位同学成绩较为优秀,他们在六次赛前测试中的成绩(单位:分)如下表所示.
19. 某学校为选拔数学能力突出的学生参加中学生数学竞赛,组织了多次测试,其中甲乙两位同学成绩较为优秀,他们在六次赛前测试中的成绩(单位:分)如下表所示.甲
80
75
90
64
88
95
乙
84
80
88
76
79
85
如果根据这六次成绩选拔其中一人参加比赛,你认为哪一位比较合适?为什么?
20. 如图,在△ABC中,CD⊥AB于D , AC=20,BC=15,DB=9. (1)、求CD , AD的值;(2)、判断△ABC的形状,并说明理由.21. 如图,直线y1=x+1交x、y轴于点A、B,直线y2=﹣2x+4交x、y轴与C、D,两直线交于点E.
(1)、求CD , AD的值;(2)、判断△ABC的形状,并说明理由.21. 如图,直线y1=x+1交x、y轴于点A、B,直线y2=﹣2x+4交x、y轴与C、D,两直线交于点E.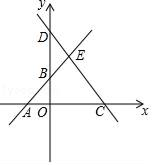 (1)、求点E的坐标;(2)、求△ACE的面积.22. 现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.(1)、请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;(2)、小明选择哪家快递公司更省钱?23. 在矩形 中, .
(1)、求点E的坐标;(2)、求△ACE的面积.22. 现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.(1)、请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;(2)、小明选择哪家快递公司更省钱?23. 在矩形 中, . (1)、P为 边上的一点,如图,将 沿直线翻折至 的位置(点B落在点E处)
(1)、P为 边上的一点,如图,将 沿直线翻折至 的位置(点B落在点E处)①当点E落在 边上时,直接写出此时 的长度 ▲ .
②若点P为 的中点,连接 ,则 与 有何位置关系?请说明理由;
(2)、点Q为射线 上的一个动点,将 沿 翻折,点D恰好落在直线 上的点 处,求 的长为 .