安徽省亳州市2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-19 类型：期末考试

进入出卷网下载

一、单选题

1. 下列根式中是最简二次根式的是（）

A、 $\sqrt{\frac{2}{3}}$ B、 $\sqrt{3}$ C、 $\sqrt{9}$ D、 $\sqrt{12}$

查看试题解析
2. 甲、乙、丙、丁四人各进行了10次射击测试，他们的平均成绩相同，方差分别是s_甲²＝0.6，s_乙²＝1.1，s_丙²＝1.2，s_丁²＝0.9，则射击成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
3. 如图，P是面积为S的 $▱ A B C D$ 内任意一点， $△ P A D$ 的面积为 $S_{1}$ ， $△ P B C$ 的面积为 $S_{2}$ ，则（）

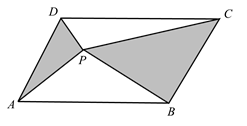A、 $S_{1} + S_{2} > \frac{S}{2}$ B、 $S_{1} + S_{2} < \frac{S}{2}$ C、 $S_{1} + S_{2} = \frac{S}{2}$ D、 $S_{1} + S_{2}$ 的大小与P点位置有关

查看试题解析
4. 若关于 $x$ 的方程 $x^{2} + 3 x + a = 0$ 有一个根为-1，则 $a$ 的值为（）

A、-4 B、-2 C、2 D、4

查看试题解析
5. 以下列各组数为边长，不能构成直角三角形的是（）

A、3，4，5 B、9，12，15 C、0.3，0.4，0.5 D、 $\sqrt{3}$ ， $\sqrt{4}$ ， $\sqrt{5}$

查看试题解析
6. 一个多边形的每一个内角都等于 $140^{\circ}$ ，那么这个多边形的边数是 $($ $)$

A、9条 B、8条 C、7条 D、6条

查看试题解析
7. 已知四边形ABCD中有四个条件：AB∥CD，AB=CD，BC∥AD，BC=AD，从中任选两个，不能使四边形ABCD成为平行四边形的选法是（）

A、AB∥CD，AB=CD B、AB∥CD，BC∥AD C、AB∥CD，BC=AD D、AB=CD，BC=AD

查看试题解析
8. 某机械厂七月份生产零件50万个，计划八、九月份共生产零件115.5万个，设八、九月份平均每月的增长率为x，那么x满足的方程是（　　）

A、50（1+x）²=115.5 B、50+50（1+x）+50（1+x）²=115.5 C、50（1+x）+50（1+x）²=115.5 D、50+50（1+x）+50（1+2x）=115.5

查看试题解析
9. 为了了解某校学生的课外阅读情况，随机抽查了10学生周阅读用时数，结果如下表：
周阅读用时数（小时）
4
5
8
12
学生人数（人）
3
4
2
1
则关于这10名学生周阅读所用时间，下列说法正确的是（　　）

A、中位数是6.5 B、众数是12 C、平均数是3.9 D、方差是6

查看试题解析
10. 如图，在四边形 $A B C D$ 中， $∠ A = 90^{°} ， A B = 3 \sqrt{2} ， A D = \sqrt{7}$ ，点 $M ， N$ 分别为线段 $B C ， A B$ 上的动点(含端点，但点 $M$ 不与点 $B$ 重合)，点 $E ， F$ 分别为 $D M ， M N$ 的中点，则 $E F$ 长度的最大值为（）

A、 $\sqrt{7}$ B、2.5 C、5 D、3.5

查看试题解析

二、填空题

11. 若二次根式 $\sqrt{2 - x}$ 有意义，则x的取值范围是．

查看试题解析
12. 把x²+2x﹣2＝0化为（x+m）²＝k的形式（m ， k为常数），则m+k＝．

查看试题解析
13. 《九章算术》中记载：“今有竹高一丈，未折抵地，去根三尺，问折者高几何？”译文：有一根竹子原高一丈（1丈=10尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？我们用线段OA和线段AB来表示竹子，其中线段AB表示竹子折断部分，用线段OB表示竹梢触地处离竹根的距离，则竹子折断处离地面的高度OA是尺．

查看试题解析
14. 如图，矩形ABCD中，AB＝6，BC＝8，点E是BC边上一点，连接AE ，将 $△$ ABE沿AE折叠，使点B落在点 $B'$ 处．

(1)、若 $∠ C E B'$ ＝70°，则∠DA $B'$ 的大小等于．

(2)、若点 $B'$ 恰好在矩形ABCD的对角线AC上，则BE的长为．

查看试题解析

三、解答题

15. 计算：（ $\sqrt{3}$ +2）（ $\sqrt{3}$ ﹣2）﹣ $\sqrt{\frac{1}{2}}$ × $\sqrt{12} + \sqrt{6}$

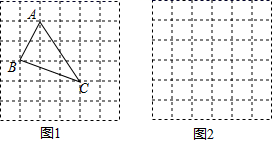
查看试题解析
16. 解方程：2x²＝3x－1

查看试题解析
17. 已知x₁ ， x₂是关于x的一元二次方程x²﹣4x+m＝0的两个实数根．

(1)、求m的取值范围；

(2)、若x₁+x₂﹣x₁x₂＝1，计算m的值．

查看试题解析
18. 在进行二次根式的运算时，如遇到 $\frac{2}{\sqrt{3} + 1}$ 这样的式子，还需做进一步的化简： $\frac{2}{\sqrt{3} + 1} = \frac{2 (\sqrt{3} - 1)}{(\sqrt{3} + 1) \times (\sqrt{3} - 1)} = \frac{2 (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1^{2}} = \frac{2 (\sqrt{3} - 1)}{3 - 1} = \sqrt{3}$ ﹣1．这种化去分母中根号的运算叫分母有理化．

(1)、请参照以上方法化简 $\frac{1}{\sqrt{5} + \sqrt{3}}$ ；

(2)、计算 $\frac{1}{\sqrt{2021} + \sqrt{2019}} + \frac{1}{\sqrt{2019} + \sqrt{2017}} + \frac{1}{\sqrt{2017} + \sqrt{2015}} + \dots + \frac{1}{\sqrt{3} + 1}$ ．

查看试题解析
19. 已知在 $△ A B C$ 中，AB ， BC ， AC三边的长分别为 $\sqrt{5}$ ， $\sqrt{10}$ ， $\sqrt{13}$ ，如图所示是小辉同学在正方形网格中 $($ 每个小正方形的边长为 $1)$ ，画出的格点 $△ A B C (△ A B C$ 的三个顶点都在正方形的顶点处 $)$ 请你参照小辉的方法在图2的正方形网格图中画出格点三角形 $△ D E F$ ，使得DE、EF、DF三边的长分别为 $\sqrt{2}$ 、 $\sqrt{8}$ 、 $\sqrt{10}$ ，然后 $①$ 判断 $△ D E F$ 的形状，说明理由 $. ②$ 求这个三角形的面积．

查看试题解析
20. 如图，在菱形ABCD中，对角线AC，BD相交于点O，E是CD的中点，连接OE.过点C作CF//BD交OE的延长线于点F，连接DF.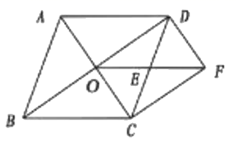

求证：

(1)、△ODE≌△FCE；

(2)、四边形OCFD是矩形。

查看试题解析

21. 为弘扬中华传统文化，某校组织八年级1000名学生参加汉字听写大赛．为了解学生整体听写能力，从中抽取部分学生的成绩(得分取正整数，满分为100分)进行统计分析，请根据尚未完成的下列图表，解答下列问题：

组别	分数段	频数	频率
一	50.5～60.5	16	0.08
二	60.5～70.5	30	0.15
三	70.5～80.5	m	0.25
四	80.5～90.5	80	n
五	90.5～100.5	24	0.12

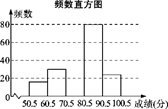(1)、写出表中：m，n，此样本中成绩的中位数落在第几组内；

(2)、补全频数直方图；

(3)、若成绩超过80分为优秀，该校八年级学生中汉字听写能力优秀的约有多少人？

查看试题解析

22. 某童装专卖店在销售中发现，一款童装每件进价为80元，销售价为120元时，每天可售出20件，为了迎接“六一”儿童节，商店决定采取适当的降价措施，以扩大销售量增加利润，经市场调查发现，如果每件童装降价1元，那么平均可多售出2件．

(1)、每件童装降价多少元时，能让利于顾客并且商家平均每天能赢利1200元．

(2)、要想平均每天赢利2000元，可能吗？请说明理由．

查看试题解析
23. 如图

（问题情境）

如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM ．

(1)、（探究展示）
证明：AM=AD+MC；

(2)、AM=DE+BM是否成立？若成立，请给出证明；若不成立，请说明理由．

(3)、（拓展延伸）
若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，探究展示(1)、(2)中的结论是否成立？请分别作出判断，不需要证明．

查看试题解析

周阅读用时数（小时）	4	5	8	12
学生人数（人）	3	4	2	1