山西省运城市芮城县2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2021-08-19 类型：期末考试

进入出卷网下载

一、单选题

1. $2 \sin 60 ° + \sqrt{3}$ 等于（）

A、 $2 \sqrt{3}$ B、2 C、3 D、 $3 \sqrt{3}$

查看试题解析
2. 抛物线y=（x﹣2）²﹣3的顶点坐标是（）

A、（2，﹣3） B、（﹣2，3） C、（2，3） D、（﹣2，﹣3）

查看试题解析
3. 如图，小明同学将一个圆锥和一个三棱柱组成组合图形，观察其三视图，其俯视图是（）

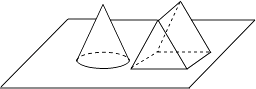A、 B、 C、 D、

查看试题解析
4. 如图，在 $▱ A B C D$ 中，E为 $C D$ 上一点，连接 $A E$ 、 $B D$ ，且 $A E$ 、 $B D$ 交于点F， $D E ： A B = 2 ： 5$ ，则 $D F ： B F$ 等于（）

A、 $2 ： 5$ B、 $2 ： 3$ C、 $3 ： 5$ D、 $3 ： 2$

查看试题解析
5. 一元二次方程x²+4x＝5配方后可变形为（）

A、（x+2）²＝5 B、（x+2）²＝9 C、（x﹣2）²＝9 D、（x﹣2）²＝21

查看试题解析
6. 在平面直角坐标系中，反比例函数 $y = \frac{3 - m}{x}$ 的图象经过第一、三象限，则m的取值范围是（）

A、 $m > 3$ B、 $m < 3$ C、 $m > - 3$ D、 $m < - 3$

查看试题解析
7. 第一中学九年级有340名学生，现对他们的生日进行统计（可以不同年），下列说法正确的是（）

A、至少有两人生日相同 B、不可能有两人生日相同 C、可能有两人生日相同，且可能性较大 D、可能有两人生日相同，但可能性较小

查看试题解析
8. 某河堤横断面如图所示，堤高 $B C = 10$ 米，迎水坡 $A B$ 的坡比是 $1 ： \sqrt{3}$ （坡比是坡面的铅直高度 $B C$ 与水平宽度 $A C$ 之比），则 $A C$ 的长是（）

A、 $10 \sqrt{3}$ 米 B、20米 C、 $20 \sqrt{3}$ 米 D、30米

查看试题解析
9. 如图，在正方形 $A B C D$ 中， $Δ A D E$ 绕点 $A$ 顺时针旋转 $90 °$ 后与 $Δ A B F$ 重合， $C F = 6$ ， $C E = 4$ ，则 $A C$ 的长度为（）

A、4 B、 $4 \sqrt{2}$ C、5 D、 $5 \sqrt{2}$

查看试题解析
10. 在平面直角坐标系中，二次函数 $y = a x^{2} + b x + c$ （ $a \neq 0$ ）的图象如图所示，现给出以下结论：① $a b c > 0$ ；② $b + 2 a = 0$ ；③ $9 a - 3 b + c = 0$ ；④ $a - b + c ⩽ a m^{2} + b m + c$ （ $m$ 为实数）其中结论错误的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 反比例函数 $y = \frac{m}{x}$ （ $m \neq 0$ ）的图象如图所示，点A为图象上的一点，过点A作 $A B ⊥ x$ 轴， $A C ⊥ y$ 轴，若四边形 $A C O B$ 的面积为4，则m的值为.

查看试题解析
12. 若关于x的方程 $x^{2} + 5 x + k = 0$ 的一个根是1，则k的值为.

查看试题解析
13. 将抛物线 $y = {(x + 1)}^{2}$ 向右平移2个单位长度，则所得抛物线对应的函数表达式为.

查看试题解析
14. 如图，在四边形 $A B C D$ 中， $∠ B = 90 °$ ， $A B = 2$ ， $C D = 8$ ， $A C ⊥ C D$ .若 $\sin ∠ A C B = \frac{1}{3}$ ，则 $\tan D =$ .

查看试题解析
15. 一块含有 $30 °$ 角的直角三角板 $A B C$ 按如图所示的方式放置，若顶点A的坐标为 $(0 ， 1)$ ，直角顶点C的坐标为 $y (- \sqrt{3} ， 0)$ ，则点B的坐标为.

查看试题解析

三、解答题

16.

(1)、解方程： $5 x (x + 3) = 2 (x + 3)$ .

(2)、计算： $\sqrt{2} \sin 45 ° - \cos^{2} 30 ° + \sin 60 ° \cdot \tan 30 °$ .

查看试题解析
17. 欢欢放学回家看到桌上有三个礼包，是爸爸送给欢欢和姐姐的礼物，其中A礼包是芭比娃娃，B和C礼包都是智能对话机器人.这些礼包用外表一样的包装盒装着，看不到里面的礼物.

(1)、欢欢随机地从桌上取出一个礼包，取出的是芭比娃娃的概率是多少？

(2)、请用树状图或列表法表示欢欢随机地从桌上取出两个礼包的所有可能结果，并求取出的两个礼包都是智能对话机器人的概率.

查看试题解析
18. 如图，反比例函数 $y = \frac{k}{x}$ （ $k \neq 0$ ）的图象与一次函数 $y = a x + b$ 的图象交于 $A (1 ， 3)$ ， $B (- 3 ， m)$ 两点.

(1)、分别求出反比例函数与一次函数的表达式.

(2)、当反比例函数的值大于一次函数的值时，请根据图象直接写出x的取值范围.

查看试题解析
19. 如图，某居民楼 $A B$ 的前面有一围墙 $C D$ ，在点E处测得楼顶A的仰角为 $25 °$ ，在F处测得楼顶A的仰角为 $45 °$ ，且 $C E$ 的高度为2米， $C F$ 之间的距离为20米（B，F，C在同一条直线上）.

(1)、求居民楼 $A B$ 的高度.

(2)、请你求出A、E两点之间的距离.（参考数据： $\sin 25 ° \approx 0.42$ ， $\cos 25 ° \approx 0.91$ ， $\tan 25 ° \approx 0.47$ ，结果保留整数）

查看试题解析
20. 某游乐场试营业期间，每天运营成本为1000元.经统计发现，每天售出的门票张数y（张）与门票售价x（元/张）之间满足一次函数 $y = - 4 x + 200$ ，设游乐场每天的利润为w（元）.（利润=票房收入－运营成本）

(1)、试求w与x之间的函数表达式.

(2)、游乐场将门票售价定为多少元/张时，每天获利最大？最大利润是多少元？

查看试题解析
21. 教育部基础教育司负责人解读“2020新中考”时强调要注重学生分析与解决问题的能力，要增强学生的创新精神和综合素质.王老师想尝试改变教学方法，将以往教会学生做题改为引导学生会学习.于是她在菱形的学习中，引导同学们解决菱形中的一个问题时，采用了以下过程（请解决王老师提出的问题）：

(1)、先出示问题：如图1，在等边三角形 $A B C$ 中，D为 $B C$ 上一点，E为 $A C$ 上一点，如果 $B D = C E$ ，连接 $A D$ 、 $B E$ ， $A D$ 、 $B E$ 相交于点P，求 $∠ A P E$ 的度数.

(2)、通过学习，王老师请同学们说说自己的收获.小明说发现一个结论：在这个等边三角形 $A B C$ 中，只要满足 $B D = C E$ ，则 $∠ A P E$ 的度数就是一个定值，不会发生改变.紧接着王老师出示了问题（2）：如图2，在菱形 $A B C D$ 中， $∠ A = 60 °$ ，E为 $B C$ 上一点，F为 $C D$ 上一点， $B E = C F$ ，连接 $D E$ 、 $B F$ ， $D E$ 、 $B F$ 相交于点P，如果 $D P = 4$ ， $B P = 3$ ，求出菱形的边长.

(3)、问题（3）：通过以上的学习请写出你得到的启示（一条即可）.

查看试题解析
22. 在学习了矩形后，数学活动小组开展了探究活动.如图1，在矩形 $A B C D$ 中， $A B = 4 \sqrt{3}$ ， $B C = 8$ ，点E在 $A D$ 上，先以 $B E$ 为折痕将A点往右折，如图2所示，再过点A作 $A F ⊥ C D$ ，垂足为F，如图3所示.

(1)、在图3中，若 $∠ B E A = 60 °$ ，则 $∠ A B C$ 的度数为， $A E$ 的长度为.

(2)、在（1）的条件下，求 $A F$ 的长.

(3)、在图3中，若 $\sin ∠ A B C = \frac{1}{4}$ ，则 $A F =$ .

查看试题解析
23. 如图，直线 $y = - x + 4$ 交x轴于点A，交y轴于点C，抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 经过点A，交y轴于点 $B (0 ， - 2)$ ，点D为抛物线上一动点，过点D作x轴的垂线，交直线 $A C$ 于点P，设点D的横坐标为 $m$ .

(1)、求抛物线的解析式.

(2)、当点D在直线 $A C$ 下方的抛物线上运动时，求出 $P D$ 长度的最大值.

(3)、当以B，C，P为顶点的三角形是等腰三角形时，求此时m的值.

查看试题解析