山西省阳泉市盂县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 点 关于原点的对称点坐标是( )A、 B、 C、 D、2. 关于x的一元二次方程x2+kx﹣2=0(k为实数)根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定3. 下列二次函数中,顶点坐标为(-5,0),且开口方向、形状与y=-x2的图象相同的是( )A、y=(x-5)2 B、y=x2-5 C、y=-(x+5)2 D、y=(x+5)24. 如图,在 的正方形网格中,每个小正方形的边长都是 , 的顶点都在这些小正方形的顶点上,则 的值为( )
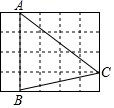 A、 B、 C、 D、5. 反比例函数 ,下列说法错误的是( )A、图象经过点(1,-3) B、图象位于第二、四象限 C、图象关于直线y=x对称 D、y随x的增大而增大6. 小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
A、 B、 C、 D、5. 反比例函数 ,下列说法错误的是( )A、图象经过点(1,-3) B、图象位于第二、四象限 C、图象关于直线y=x对称 D、y随x的增大而增大6. 小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
 A、 B、 C、 D、7. 李老师在编写下面这个题目的答案时,不小心打乱了解答过程的顺序,你能帮他调整过来吗?证明步骤正确的顺序是( )
A、 B、 C、 D、7. 李老师在编写下面这个题目的答案时,不小心打乱了解答过程的顺序,你能帮他调整过来吗?证明步骤正确的顺序是( )
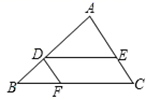 A、③②①④ B、②④①③ C、③①④② D、②③④①8. 全等图形是相似比为1的相似图形,因此全等是特殊的相似,我们可以由研究全等三角形的思路,提出相似三角形的问题和研究方法.这种其中主要利用的数学方法是( )A、代入法 B、列举法 C、从特殊到一般 D、反证法9. 已知 ,一次函数 与反比例函数 在同一直角坐标系中的图象可能( )A、
A、③②①④ B、②④①③ C、③①④② D、②③④①8. 全等图形是相似比为1的相似图形,因此全等是特殊的相似,我们可以由研究全等三角形的思路,提出相似三角形的问题和研究方法.这种其中主要利用的数学方法是( )A、代入法 B、列举法 C、从特殊到一般 D、反证法9. 已知 ,一次函数 与反比例函数 在同一直角坐标系中的图象可能( )A、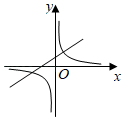 B、
B、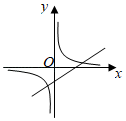 C、
C、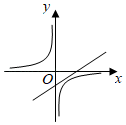 D、
D、 10. 阅读理解:已知两点 ,则线段 的中点 的坐标公式为: , .如图,已知点 为坐标原点,点 , 经过点 ,点 为弦 的中点.若点 ,则有 满足等式: .设 ,则 满足的等式是( )
10. 阅读理解:已知两点 ,则线段 的中点 的坐标公式为: , .如图,已知点 为坐标原点,点 , 经过点 ,点 为弦 的中点.若点 ,则有 满足等式: .设 ,则 满足的等式是( )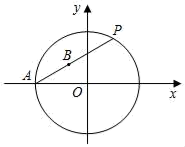 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
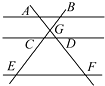
11. 如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么 的值等于 .
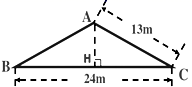
 12. 某一建筑物的楼顶是“人”字型,并铺上红瓦装饰.现知道楼顶的坡度超过0.5时,瓦片会滑落下来.请你根据图中数据判断这一楼顶铺设的瓦片是否会滑落下来? . (填“会”或“不会”)
12. 某一建筑物的楼顶是“人”字型,并铺上红瓦装饰.现知道楼顶的坡度超过0.5时,瓦片会滑落下来.请你根据图中数据判断这一楼顶铺设的瓦片是否会滑落下来? . (填“会”或“不会”)
 13. 在平面直角坐标系中,点 的坐标分别是 ,以点 为位似中心,相们比为 ,把 缩小,得到 ,则点 的对应点 的坐标为.14. 若点A(﹣4,y1)、B(﹣2,y2)、C(2,y3)都在反比例函数 的图象上,则y1、y2、y3的大小关系是 .15. 如图,菱形AD的边长为2,对角线AC、BD相交于点O , BD=2,分别以AB、BC为直径作半圆,则图中阴影部分的面积为 .
13. 在平面直角坐标系中,点 的坐标分别是 ,以点 为位似中心,相们比为 ,把 缩小,得到 ,则点 的对应点 的坐标为.14. 若点A(﹣4,y1)、B(﹣2,y2)、C(2,y3)都在反比例函数 的图象上,则y1、y2、y3的大小关系是 .15. 如图,菱形AD的边长为2,对角线AC、BD相交于点O , BD=2,分别以AB、BC为直径作半圆,则图中阴影部分的面积为 .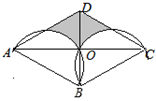
三、解答题
-
16. 计算:(1)、sin30°-(5- tan75°)0 ;(2)、3 tan230°- sin45°+ sin60°.17. 在 中, .
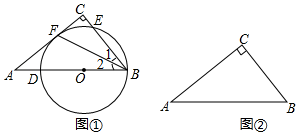 (1)、如图①,点 在斜边 上,以点 为圆心, 长为半径的圆交 于点 ,交 于点 ,与边 相切于点 .求证: ;(2)、在图②中作 ,使它满足以下条件:
(1)、如图①,点 在斜边 上,以点 为圆心, 长为半径的圆交 于点 ,交 于点 ,与边 相切于点 .求证: ;(2)、在图②中作 ,使它满足以下条件:①圆心在边 上;②经过点 ;③与边 相切.
(尺规作图,只保留作图痕迹,不要求写出作法)
18. 为落实立德树人的根本任务,加强思改、历史学科教师的专业化队伍建设.某校计划从前来应聘的思政专业(一名研究生,一名本科生)、历史专业(一名研究生、一名本科生)的高校毕业生中选聘教师,在政治思想审核合格的条件下,假设每位毕业生被录用的机会相等(1)、若从中只录用一人,恰好选到思政专业毕业生的概率是:(2)、若从中录用两人,请用列表或画树状图的方法,求恰好选到的是一名思政研究生和一名历史本科生的概率.19. 如图,在平面直角坐标系xOy中,反比例函数 的图象过等边三角形BOC的顶点B, OC=2,点A在反比例函数图象上,连接AC,AO.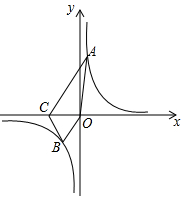 (1)、求反比例函数 的表达式;(2)、若四边形ACBO的面积是 ,求点A的坐标.20. 全国第二届青年运动会是山西省历史上第一次举办的大型综合性运动会,太原作为主赛区,新建了很多场馆,其中在汾河东岸落成了太原水上运动中心,它的终点塔及媒体中心是一个以“大帆船”造型(如图1),外观极具创新,这里主要承办赛艇、皮划艇、龙舟等项目的比赛.“青春”数学兴趣小组为了测量“大帆船”AB的长度,他们站在汾河西岸,在与AB平行的直线l上取了两个点C、D , 测得CD=40m,∠CDA=120°,∠ACB=18.5°,∠BCD=26.5°,如图2.请根据测量结果计算“大帆船”AB的长度.(结果精确到0.1m,参考数据:sin26.5°≈0.45,tan26.5°≈0.50, ≈1.41, ≈1.73)
(1)、求反比例函数 的表达式;(2)、若四边形ACBO的面积是 ,求点A的坐标.20. 全国第二届青年运动会是山西省历史上第一次举办的大型综合性运动会,太原作为主赛区,新建了很多场馆,其中在汾河东岸落成了太原水上运动中心,它的终点塔及媒体中心是一个以“大帆船”造型(如图1),外观极具创新,这里主要承办赛艇、皮划艇、龙舟等项目的比赛.“青春”数学兴趣小组为了测量“大帆船”AB的长度,他们站在汾河西岸,在与AB平行的直线l上取了两个点C、D , 测得CD=40m,∠CDA=120°,∠ACB=18.5°,∠BCD=26.5°,如图2.请根据测量结果计算“大帆船”AB的长度.(结果精确到0.1m,参考数据:sin26.5°≈0.45,tan26.5°≈0.50, ≈1.41, ≈1.73)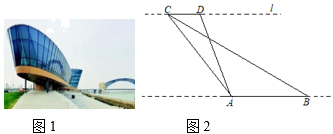 21. 阅读下列材料,并完成相应的任务.
21. 阅读下列材料,并完成相应的任务. (1)、任务:
(1)、任务:上述证明过程中的“依据1”和“依据2”分别指什么?
依据1:
依据2:
(2)、当圆内接四边形ABCD是矩形时,托勒密定理就是我们非常熟知的一个定理: (请写出定理名称).(3)、如图(3),四边形ABCD内接于⊙O , AB=3,AD=5,∠BAD=60°,点C是弧BD的中点,求AC的长.22. 如图1,在 中,∠B=90°, ,点D,E分别是边BC,AC的中点,连接 将 绕点C按顺时针方向旋转,记旋转角为 . (1)、问题发现:
(1)、问题发现:当 时, ; 当 时, .
(2)、拓展探究:试判断:当 时, 的大小有无变化?请仅就图2的情况给出证明.
(3)、问题解决:当 旋转至A、D、E三点共线时,直接写出线段BD的长.
23. 如图, 已知抛物线 的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 . (1)、求抛物线的解析式和A、B两点的坐标;(2)、若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),则是否存在一点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积;若不存在,试说明理由;(3)、若M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求M点的坐标 .
(1)、求抛物线的解析式和A、B两点的坐标;(2)、若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),则是否存在一点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积;若不存在,试说明理由;(3)、若M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求M点的坐标 .