山西省吕梁市汾阳市2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 下列式子中表示y是x的反比例函数的是( )A、 B、 C、 D、2. 下列图形中一定是相似形的是( )A、两个菱形 B、两个等边三角形 C、两个矩形 D、两个直角三角形3. 若 ∽ , , , ,则 的长为( )A、4 B、5 C、6 D、74. 已知关于x的一元二次方程 有两个相等的实数根,则a的值是( )A、4 B、﹣4 C、1 D、﹣15. 将抛物线 向上平移两个单位长度,得到的抛物线解析式是( )A、 B、 C、 D、6. 下列事件是必然事件的是( )A、打开电视播放建国70周年国庆阅兵式 B、任意翻开初中数学书一页,内容是实数练习 C、去领奖的三位同学中,其中有两位性别相同 D、食用保健品后长生不老7. 根据圆规作图的痕迹,可用直尺成功找到三角形外心的是( )A、
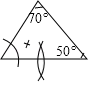 B、
B、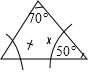 C、
C、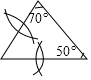 D、
D、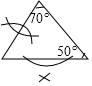 8. 刘徽是我国古代一位伟大的数学家,他的杰作《九章算术注》和《海宝算经》是中国宝贵的文化遗产.他所提出的割圆术可以估算圆周率 .割圆术是依次用圆内接正六边形、正十二边形…去逼近圆.如图, 的半径为1,则 的内接正十二边形面积为( )
8. 刘徽是我国古代一位伟大的数学家,他的杰作《九章算术注》和《海宝算经》是中国宝贵的文化遗产.他所提出的割圆术可以估算圆周率 .割圆术是依次用圆内接正六边形、正十二边形…去逼近圆.如图, 的半径为1,则 的内接正十二边形面积为( )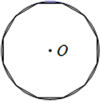 A、1 B、3 C、3.1 D、3.149. 定义:如果一个一元二次方程的两个实数根的比值与另一个一元二次方程的两个实数根的比值相等,我们称这两个方程为“相似方程”,例如, 的实数根是3或6, 的实数根是1或2, ,则一元二次方程 与 为相似方程.下列各组方程不是相似方程的是( )A、 与 B、 与 C、 与 D、 与10. 如图,某幢建筑物从2.25米高的窗口A用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面3米,则水流下落点B离墙的距离OB是( )
A、1 B、3 C、3.1 D、3.149. 定义:如果一个一元二次方程的两个实数根的比值与另一个一元二次方程的两个实数根的比值相等,我们称这两个方程为“相似方程”,例如, 的实数根是3或6, 的实数根是1或2, ,则一元二次方程 与 为相似方程.下列各组方程不是相似方程的是( )A、 与 B、 与 C、 与 D、 与10. 如图,某幢建筑物从2.25米高的窗口A用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面3米,则水流下落点B离墙的距离OB是( )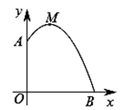 A、2.5米 B、3米 C、3.5米 D、4米
A、2.5米 B、3米 C、3.5米 D、4米二、填空题
-
11. 写出一个二次函数关系式,使其图象开口向上.12. 反比例函数 的图象在第象限.13. 近日,某市推出名师公益大课堂.据统计,第一批公益课受益学生2万人次,第三批公益课受益学生2.42万人次.如果第二批,第三批公益课受益学生人次的增长率相同,则这个增长率是.14. 如图,A,B,C是 上的三个点,四边形 是平行四边形,连接 , ,若 ,则 .
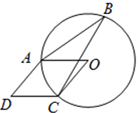 15. 如图,在 中 , , ,以 为直角边、A为直角顶点作等腰直角三角形 ,则 .
15. 如图,在 中 , , ,以 为直角边、A为直角顶点作等腰直角三角形 ,则 .
三、解答题
-
16. 解方程:(1)、(2)、17. 如图,在平面直角坐标系中, 的顶点坐标分别为 , , .

⑴将 以原点 为旋转中心旋转 得到 ,画出旋转后的 .
⑵平移 ,使点A的对应点 坐标为 ,画出平移后的
⑶若将 绕某一点旋转可得到 ,请直接写出旋转中心的坐标.
18. “共和国勋章”是中华人民共和国的最高荣誉勋章,在2019年获得“共和国勋章”的八位杰出人物中,有于敏、孙家栋、袁隆平、黄旭华四位院士.如图是四位院士(依次记为A、B、C、D).为让同学们了解四位院士的贡献,老师设计如下活动:取四张完全相同的卡片,分别写上A、B、C、D四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应院士的资料,并做成小报.(1)、班长在四种卡片中随机抽到标号为C的概率为.(2)、请用画树状图或列表的方法求小明和小华查找不同院士资料的概率. 19. 如图,一次函数 与反比例函数 的图象交于 ,点 两点,交x轴于点C.
19. 如图,一次函数 与反比例函数 的图象交于 ,点 两点,交x轴于点C.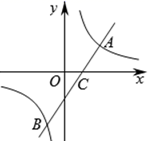 (1)、求m、n的值.(2)、请根据图象直接写出不等式 的解集.(3)、x轴上是否存在一点D,使得以A、C、D三点为顶点的三角形是 为腰的等腰三角形,若存在,请直接写出符合条件的点D的坐标,若不存在,请说明理由.20. 如图, 是 的直径, 是 的切线,切点为A, 交 于点D,点E是 的中点.
(1)、求m、n的值.(2)、请根据图象直接写出不等式 的解集.(3)、x轴上是否存在一点D,使得以A、C、D三点为顶点的三角形是 为腰的等腰三角形,若存在,请直接写出符合条件的点D的坐标,若不存在,请说明理由.20. 如图, 是 的直径, 是 的切线,切点为A, 交 于点D,点E是 的中点. (1)、试判断直线 与 的位置关系,并说明理由;(2)、若 的半径为2, , ,求图中阴影部分的周长.21. 超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加 元,每天售出 件.(1)、请写出 与 之间的函数表达式;(2)、当 为多少时,超市每天销售这种玩具可获利润2250元?(3)、设超市每天销售这种玩具可获利 元,当 为多少时 最大,最大值是多少?22. 综合与实践(1)、问题情境
(1)、试判断直线 与 的位置关系,并说明理由;(2)、若 的半径为2, , ,求图中阴影部分的周长.21. 超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加 元,每天售出 件.(1)、请写出 与 之间的函数表达式;(2)、当 为多少时,超市每天销售这种玩具可获利润2250元?(3)、设超市每天销售这种玩具可获利 元,当 为多少时 最大,最大值是多少?22. 综合与实践(1)、问题情境数学课上,李老师提出了这样一个问题:如图1,点P是正方形 内一点, , , .你能求出 的度数吗?

小敏与同桌小聪通过观察、思考、讨论后,得出了如下思路:
思路一:将 绕点B逆时针旋转 ,得到 ,连接 ,求出 的度数.
思路二:将 绕点B顺时针旋转 ,得到 ,连接 ,求出 的度数.
请参考以上思路,任选一种写出完整的解答过程.
(2)、思路二、同思路一的方法.类比探究
如图2,若点P是正方形 外一点, , , ,求 的度数.
(3)、拓展应用如图3,在边长为 的等边三角形 内有一点 , , ,则 的面积是.
23. 综合与探究如图,已知抛物线 与x轴交于 , 两点,与y轴交于点C,对称轴为直线l,顶点为D.
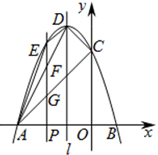 (1)、求抛物线的解析式及点D坐标;(2)、在直线l上是否存在一点M,使点M到点B的距离与到点C的距离之和最小?若存在,求出点M的坐标;若不存在,请说明理由.(3)、在x轴上取一动点 , ,过点P作x轴的垂线,分别交抛物线, , 于点E,F,G.
(1)、求抛物线的解析式及点D坐标;(2)、在直线l上是否存在一点M,使点M到点B的距离与到点C的距离之和最小?若存在,求出点M的坐标;若不存在,请说明理由.(3)、在x轴上取一动点 , ,过点P作x轴的垂线,分别交抛物线, , 于点E,F,G.①判断线段 与 的数量关系,并说明理由
②连接 , , ,当m为何值时,四边形 的面积最大?最大值为多少?