山西省临汾市襄汾县2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2021-08-19 类型：期末考试

进入出卷网下载

一、单选题

1. 若式子 $\frac{1}{\sqrt{x - 3}}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x \geq 3$ B、 $x \leq 3$ C、 $x > 3$ D、 $x < 3$

查看试题解析
2. 已知抛物线y=x²－8x+c的顶点在x轴上，则c的值是（）

A、16 B、-4 C、4 D、8

查看试题解析
3. 下列说法正确的是（）

A、随机抛掷一枚均匀的硬币，落地后反面一定朝上 B、从1，2，3，4，5中随机取一个数，取得奇数的可能性较大 C、某彩票中奖率为36%，说明买100张彩票，有36张中奖 D、打开电视，中央一套正在播放新闻联播

查看试题解析
4. 在Rt△ABC中，∠C=90°，若斜边AB是直角边BC的3倍，则tanB的值是（　　）

A、 $\frac{1}{3}$ B、3 C、 $\frac{\sqrt{2}}{4}$ D、2 $\sqrt{2}$

查看试题解析
5. 若关于x的一元二次方程 $x^{2} + b x + c = 0$ 的两个实数根分别为 $x_{1} = - 1 ， x_{2} = 2$ ，那么抛物线 $y = x^{2} + b x + c$ 的对称轴为直线（）

A、 $x = 1$ B、 $x = \frac{1}{2}$ C、 $x = \frac{3}{2}$ D、 $x = - \frac{1}{2}$

查看试题解析
6. 如图，△OAB与△OCD是以点0为位似中心的位似图形，相似比为1：2，∠OCD=90 $°$ ，CO=CD．若B(2，0)，则点C的坐标为（）

A、(2，2) B、(1，2) C、（ $\sqrt{2}$ ，2 $\sqrt{2}$ ） D、(2，1)

查看试题解析
7. 在平面直角坐标系中，将抛物线y=x²的图象向左平移3个单位、再向下平移2个单位所得的抛物线的函数表达式为（）

A、y=(x－3)²－2 B、y=(x－3)²＋2 C、y=(x＋3)²－2 D、y=(x＋3)²＋2

查看试题解析
8. 如图，等边△ABC的边长为6，P为BC上一点，BP=2，D为AC上一点，若∠APD=60°，则CD的长为（）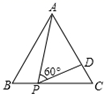

A、2 B、 $\frac{4}{3}$ C、 $\frac{2}{3}$ D、1

查看试题解析
9. 如图，在△ABC中，中线BE、CF相交于点G，连接EF，下列结论：
① $\frac{E F}{B C}$ = $\frac{1}{2}$ ； ② $\frac{S_{△ EGF}}{S_{△ CGB}}$ = $\frac{1}{2}$ ； ③ $\frac{A F}{A B}$ = $\frac{G E}{G B}$ ； ④ $\frac{S_{△ GEF}}{S_{△ AEF}}$ = $\frac{1}{3}$ ．其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c$ 的y与x的部分对应值如表：

$x$

$- 1$

$0$

$2$

$3$

$4$

$y$

$5$

$0$

$- 4$

$- 3$

$0$

下列结论： $①$ 抛物线的开口向上；②抛物线的对称轴为直线 $x = 2$ ；③当 $0 < x < 4$ 时， $y > 0$ ；④抛物线与x轴的两个交点间的距离是4；⑤若 $A (x_{1} ， 2) ， B (x_{2} ， 3)$ 是抛物线上两点，则 $x_{1} \leq x_{2}$ ，其中正确的个数是（）

A、 $2$ B、 $3$ C、 $4$ D、 $5$

查看试题解析

二、填空题

11. 已知a=3＋2 $\sqrt{2}$ ，b=3－2 $\sqrt{2}$ ，则a²b＋ab²= ．

查看试题解析
12. 毛泽东在《沁园春·雪》中提到五位历史名人：秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗.小红将这五位名人简介分别写在五张完全相同的知识卡片上.小哲从中随机抽取一张，卡片上介绍的人物是唐朝以后出生的概率是．

查看试题解析
13. 如图，∠DAB=∠CAE，请补充一个条件：，使△ABC∽△ADE.

查看试题解析
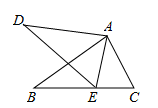14. 如图所示是二次函数 $y = a x^{2} + b x + c$ 的图象，下列结论：

①二次三项式 $a x^{2} + b x + c$ 的最大值为 $4$ ；

$②$ 使 $y \leq 3$ 成立的x的取值范围是 $x \leq - 2$ ；

$③$ 一元二次方程 $a x^{2} + b x + c = k$ ，当 $k < 4$ 时，方程总有两个不相等的实数根；

$④$ 该抛物线的对称轴是直线 $x = - 1$ ；

$⑤ 4 a - 2 b + c < 0$

其中正确的结论有 (把所有正确结论的序号都填在横线上)

查看试题解析
15. 已知△ABC中，tanB= $\frac{2}{3}$ ，BC=6，过点A作BC边上的高，垂足为点D，且满足BD：CD=2：1，则△ABC面积的所有可能值为．

查看试题解析

三、解答题

16. 计算：

(1)、 $\sqrt{48} \div \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{12} + \sqrt{24}$

(2)、 $- 3^{2} - {(π - 3.14)}^{0} + {(\tan 30^{\circ})}^{- 1} - 2 \sqrt{\frac{1}{2}} + \frac{1}{\sqrt{2} - 1}$

查看试题解析
17. 用适当方法解下列方程．

(1)、 $3 x^{2} - l = 4 x$

(2)、 $2 x (2 x + 5) = (x - l) (2 x + 5)$

查看试题解析

18. 一只不透明的袋子中装有

4

个质地、大小均相同的小球，这些小球分别标有数字

3 、 4 、 5 、 x

，甲、乙两人每次同时从袋中各随机摸出

1

个球，并计算摸出的这

2

个小球上数字之和，记录后都将小球放回袋中搅匀，进行重复实验．实验数据如下表

摸球总次数	$10$	$20$	$30$	$60$	$90$	$120$	$180$	$240$	$330$	$450$
“和为 $8$ ”出现的频数	$2$	$10$	$13$	$24$	$30$	$37$	$58$	$82$	$110$	$150$
“和为 $8$ ”出现的频率	$0.20$	$0.50$	$0.43$	$0.40$	$0.33$	$0.31$	$0.32$	$0.34$	$0.33$	$0.33$

解答下列问题：

(1)、如果实验继续进行下去，根据上表数据，出现“和为

8

”的频率将稳定在它的概率附近．估计出现“和为

8

”的概率是；

(2)、如果摸出的这两个小球上数字之和为

9

的概率是

\frac{1}{3}

，那么x的值可以取

7

吗？请用列表法或画树状图法说明理由；如果x的值不可以取

7

，请写出一个符合要求的x值．

查看试题解析

19. 已知抛物线与x轴交于点 $(1 ， 0)$ 和 $(2 ， 0)$ 且过点 $(3 ， 4)$ ．

(1)、求抛物线的解析式；

(2)、抛物线的顶点坐标；

(3)、 $x$ 取什么值时，y随x的增大而增大；x取什么值时，y随x增大而减小．

查看试题解析
20. 学了一元二次方程的根与系数的关系后，小亮兴奋地说：“若设一元二次方程 $a x^{2} + b x + c = 0$ 的两个根为 $x_{1} ， x_{2}$ ，由根与系数的关系有 $x_{1} + x_{2} = - \frac{b}{a}$ ， $x_{1} x_{2} = \frac{c}{a}$ ，由此就能快速求出 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ ， $x_{1}^{2} + x_{2}^{2}$ ，···的值了．比如设 $x_{1} ， x_{2}$ 是方程 $x^{2} + 2 x + 3 = 0$ 的两个根，则 $x_{1} + x_{2} = - 2$ ， $x_{1} x_{2} = 3$ ，得 $\frac{1}{x_{1}} + \frac{1}{x_{2}} = \frac{x_{1} + x_{2}}{x_{1} x_{2}} = - \frac{2}{3}$ ．

(1)、小亮的说法对吗？简要说明理由；

(2)、写一个你最喜欢的元二次方程，并求出两根的平方和；

(3)、已知 $2 - \sqrt{3}$ 是关于x的方程 $x^{2} - 4 x + c = 0$ 的一个根，求方程的另一个根与c的值．

查看试题解析
21. 为给邓小平诞辰 $110$ 周年献礼，广安市政府对城市建设进行了整改，如图所示，已知斜坡 $A B$ 长60 $\sqrt{2}$ 米，坡角(即 $∠ B A C$ )为 $45 °$ ， $B C ⊥ A C$ ，现计划在斜坡中点D处挖去部分斜坡，修建一个平行于水平线 $C A$ 的休闲平台 $D E$ 和一条新的斜坡 $B E$ (下面两个小题结果都保留根号).

(1)、若修建的斜坡BE的坡比为 $\sqrt{3}$ ：1，求休闲平台 $D E$ 的长是多少米？

(2)、一座建筑物 $G H$ 距离 $A$ 点 $33$ 米远(即 $A G = 33$ 米)，小亮在D点测得建筑物顶部H的仰角(即 $∠ H D M$ )为 $30 °$ .点B、C、A、G，H在同一个平面内，点C、A、G在同一条直线上，且 $H G ⊥ C G$ ，问建筑物 $G H$ 高为多少米？

查看试题解析
22. 将一副三角尺（在Rt△ABC中，∠ACB=90°，∠B=60°；在Rt△DEF中，∠EDF=90°，∠E=45°）如图1摆放，点D为AB边的中点，DE交AC于点P，DF经过点C，且BC=2.

(1)、求证：△ADC∽△APD；

(2)、求△APD的面积；

(3)、如图2，将△DEF绕点D顺时针方向旋转角α（0°＜α＜60°），此时的等腰直角三角尺记为△DE′F′，DE′交AC于点M，DF′交BC于点N，试判断 $\frac{PM}{CN}$ 的值是否随着α的变化而变化？如果不变，请求出 $\frac{PM}{CN}$ 的值；反之，请说明理由．

查看试题解析
23. 如图，抛物线 $y = {(x - 1)}^{2} + k$ 与x轴相交于 $A ， B$ 两点（点 $A$ 在点 $B$ 的左侧），与 $y$ 轴相交于点 $C (0 ， - 3)$ ． $P$ 为抛物线上一点，横坐标为 $m$ ，且 $m > 0$ ．

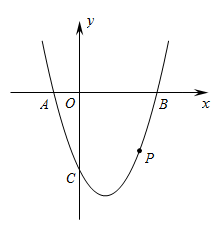(1)、求此抛物线的解析式；

(2)、当点 $P$ 位于 $x$ 轴下方时，求 $Δ A B P$ 面积的最大值；

(3)、设此抛物线在点 $C$ 与点 $P$ 之间部分（含点 $C$ 和点 $P$ ）最高点与最低点的纵坐标之差为 $h$ ．
①求 $h$ 关于 $m$ 的函数解析式，并写出自变量 $m$ 的取值范围；

②当 $h = 9$ 时，直接写出 $Δ B C P$ 的面积．

查看试题解析

$x$	$- 1$	$0$	$2$	$3$	$4$
$y$	$5$	$0$	$- 4$	$- 3$	$0$