山西省晋中市寿阳县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 抛物线y=-(x+2)2+3的顶点坐标是( )A、(-2,3) B、(2,3) C、(2,-3) D、(-2,-3)2. 如图,已知△ABC的外接圆⊙O的半径为3,AC=4,则sinB的值是( )
 A、 B、 C、 D、3. 为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B间距离的有( )
A、 B、 C、 D、3. 为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B间距离的有( )
 A、1组 B、2组 C、3组 D、4组4.
A、1组 B、2组 C、3组 D、4组4.如图点I是△ABC的内心,∠BIC=130°,则∠BAC=( )
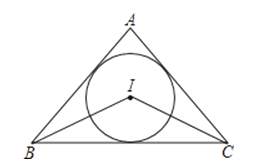 A、65° B、50° C、80° D、100°5. 已知二次函数 ,若自变量x分别取x1 , x2 , x3 , 且0<x1<x2<x3 , 则对应的函数值y1 , y2 , y3的大小关系正确的是( )A、y1>y2>y3 B、y1<y2<y3 C、y2>y3>y1 D、y2<y3<y16.
A、65° B、50° C、80° D、100°5. 已知二次函数 ,若自变量x分别取x1 , x2 , x3 , 且0<x1<x2<x3 , 则对应的函数值y1 , y2 , y3的大小关系正确的是( )A、y1>y2>y3 B、y1<y2<y3 C、y2>y3>y1 D、y2<y3<y16.如图,PA、PB分别切⊙O于A、B,PA=10cm,C是劣弧AB上的点(不与点A、B重合),过点C的切线分别交PA、PB于点E、F.则△PEF的周长为( )
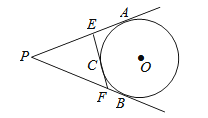 A、10cm B、15cm C、20cm D、25cm7. 如图是小李上学用的自行车,型号是24英吋(车轮的直径为24英吋,约60厘米),为了防止在下雨天骑车时的泥水溅到身上,他想在自行车两轮的阴影部分两侧装上挡水的铁皮(两个阴影部分分别是以C、D为圆心的两个扇形),量出四边形ABCD中∠DAB=125°、∠ABC=115°,那么预计需要的铁皮面积约是( )
A、10cm B、15cm C、20cm D、25cm7. 如图是小李上学用的自行车,型号是24英吋(车轮的直径为24英吋,约60厘米),为了防止在下雨天骑车时的泥水溅到身上,他想在自行车两轮的阴影部分两侧装上挡水的铁皮(两个阴影部分分别是以C、D为圆心的两个扇形),量出四边形ABCD中∠DAB=125°、∠ABC=115°,那么预计需要的铁皮面积约是( ) A、300πcm2 B、600πcm2 C、900πcm2 D、1200πcm28. 抛物线 的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为 ,则b、c的值为( )A、b=2,c=﹣6 B、b=2,c=0 C、b=﹣6,c=8 D、b=﹣6,c=29. 若二次函数y=x2+mx的图象的对称轴是直线x=3,则关于x的方程x2+mx=7的解为( )A、x1=0,x2=6 B、x1=1,x2=7 C、x1=1,x2=-7 D、x1=-1,x2=710. 如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线
A、300πcm2 B、600πcm2 C、900πcm2 D、1200πcm28. 抛物线 的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为 ,则b、c的值为( )A、b=2,c=﹣6 B、b=2,c=0 C、b=﹣6,c=8 D、b=﹣6,c=29. 若二次函数y=x2+mx的图象的对称轴是直线x=3,则关于x的方程x2+mx=7的解为( )A、x1=0,x2=6 B、x1=1,x2=7 C、x1=1,x2=-7 D、x1=-1,x2=710. 如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线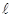 ,与⊙O过A点的切线交于点B,且∠APB=60°,设OP= x,则△PAB的面积y关于x的函数图象大致是( )
,与⊙O过A点的切线交于点B,且∠APB=60°,设OP= x,则△PAB的面积y关于x的函数图象大致是( ) 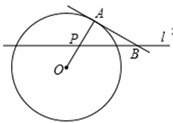 A、
A、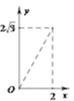 B、
B、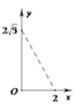 C、
C、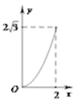 D、
D、
二、填空题
-
11. 把二次函数y=x2﹣12x化为形如y=a(x﹣h)2+k的形式12. 如图,将半径为2 cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB=.
 13. 如图,某涵洞的截面是抛物线型,现测得水面宽AB=1.6m,涵洞顶点O到水面的距离CO=2.4m,在图中直角坐标系内涵洞截面所在抛物线的表达式是.
13. 如图,某涵洞的截面是抛物线型,现测得水面宽AB=1.6m,涵洞顶点O到水面的距离CO=2.4m,在图中直角坐标系内涵洞截面所在抛物线的表达式是. 14. 已知正六边形ABCDEF内接于⊙O,图中阴影部分的面积为 ,则⊙O的半径为 .
14. 已知正六边形ABCDEF内接于⊙O,图中阴影部分的面积为 ,则⊙O的半径为 .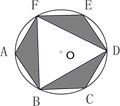 15. 如图,△ABC为等边三角形,AB=6,动点O在△ABC的边上从点A出发沿着A→C→B→A的路线匀速运动一周,速度为1个长度单位每秒,以O为圆心、 为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第秒.
15. 如图,△ABC为等边三角形,AB=6,动点O在△ABC的边上从点A出发沿着A→C→B→A的路线匀速运动一周,速度为1个长度单位每秒,以O为圆心、 为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第秒.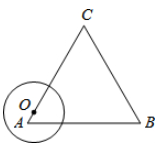
三、解答题
-
16.(1)、计算(2)、解方程17. 已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3).
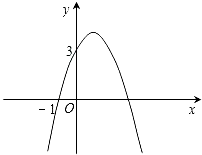 (1)、求出b,c的值,并写出此二次函数的解析式;(2)、根据图象,写出函数值y为正数时,自变量x的取值范围.18. 如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D是BC的中点.
(1)、求出b,c的值,并写出此二次函数的解析式;(2)、根据图象,写出函数值y为正数时,自变量x的取值范围.18. 如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D是BC的中点. (1)、求证:△ABC为等边三角形.(2)、求DE的长.19. 如图,在△ABC中,∠A=∠B=30°,过点C作CD⊥AC,交AB于点D.
(1)、求证:△ABC为等边三角形.(2)、求DE的长.19. 如图,在△ABC中,∠A=∠B=30°,过点C作CD⊥AC,交AB于点D.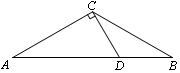 (1)、作⊙O,使⊙O经过A、C、D三点(尺规作图,保留作图痕迹,不写作法);(2)、判断直线 BC与⊙O的位置关系,并说明理由.20. 网上销售已成为产品销售的一种重要方式,很多大学生也在网上开起了网店,某手机销售网店正在代理销售一种新型智能手机,手机每部进价为1000元,经过试销发现:售价x(元/部)与每天交易量y(部)之间满足如图所示关系。
(1)、作⊙O,使⊙O经过A、C、D三点(尺规作图,保留作图痕迹,不写作法);(2)、判断直线 BC与⊙O的位置关系,并说明理由.20. 网上销售已成为产品销售的一种重要方式,很多大学生也在网上开起了网店,某手机销售网店正在代理销售一种新型智能手机,手机每部进价为1000元,经过试销发现:售价x(元/部)与每天交易量y(部)之间满足如图所示关系。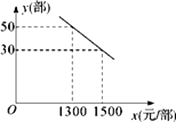 (1)、求出y与x之间的函数关系式;(2)、写出每天的利润W与销售价x之间的函数关系式.若你是网店老板,会将价格定为多少,使每天获得的利润最大,最大利润是多少?21. 某游乐场部分平面图如图所示,C,E,A在同一直线上,D,E,B在同一直线上,测得A处与E处的距离为80 m,C处与D处的距离为34 m,∠C=90°,∠ABE=90°,∠BAE=30°.( ≈1.4, ≈1.7)
(1)、求出y与x之间的函数关系式;(2)、写出每天的利润W与销售价x之间的函数关系式.若你是网店老板,会将价格定为多少,使每天获得的利润最大,最大利润是多少?21. 某游乐场部分平面图如图所示,C,E,A在同一直线上,D,E,B在同一直线上,测得A处与E处的距离为80 m,C处与D处的距离为34 m,∠C=90°,∠ABE=90°,∠BAE=30°.( ≈1.4, ≈1.7) (1)、求旋转木马E处到出口B处的距离;(2)、求海洋球D处到出口B处的距离(结果保留整数).22. 如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点,CE交⊙O于点F,连接OC、AC.
(1)、求旋转木马E处到出口B处的距离;(2)、求海洋球D处到出口B处的距离(结果保留整数).22. 如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点,CE交⊙O于点F,连接OC、AC.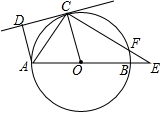 (1)、求证:AC平分∠DAO.(2)、若∠DAO=105°,∠E=30°
(1)、求证:AC平分∠DAO.(2)、若∠DAO=105°,∠E=30°①求∠OCE的度数;
②若⊙O的半径为2 ,求线段EF的长.
23. 如图,已知抛物线 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.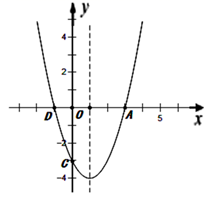 (1)、直接写出A、D、C三点的坐标;(2)、若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;(3)、设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)、直接写出A、D、C三点的坐标;(2)、若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;(3)、设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.