内蒙古自治区通辽市霍林郭勒市初中联盟校2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2021-08-19 类型：期末考试

进入出卷网下载

一、单选题

1. 观察下列图案，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列事件中，是随机事件的是（）

A、射击运动员射击一次，命中靶心 B、任意画一个三角形，其内角和是360° C、掷一次骰子，向上一面的点数大于6 D、通常加热到100℃，水沸腾

查看试题解析
3. 如图， $⊙ O$ 的直径 $A B$ 垂直于弦 $C D$ ，垂足是点 $E$ ， $∠ C A O = {22.5}^{\circ}$ ， $O C = 6$ ，则 $C D$ 的长为（）

A、 $6 \sqrt{2}$ B、 $3 \sqrt{2}$ C、6 D、12

查看试题解析
4. 如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD等于（）

A、116° B、32° C、58° D、64°

查看试题解析
5. 如图，PA、PB分别切圆O于A、B两点，C为劣弧AB上一点，∠APB=40°，则∠ACB=（）．

A、70° B、80° C、110° D、140°

查看试题解析
6. 若关于x的一元二次方程 $k x^{2} - (2 k + 1) x + k - 1 = 0$ 有两个不相等实数根，那么k的取值范围是（）

A、k＞－ $\frac{1}{4}$ 且k≠0 B、k＞－ $\frac{1}{8}$ 且k≠0 C、k≥－ $\frac{1}{8}$ 且k≠0 D、k＜－ $\frac{1}{8}$ 且k≠0

查看试题解析
7. 如图， $⊙ O$ 与正方形ABCD的两边AB ， AD相切，且DE与 $⊙ O$ 相切于点E ．若 $⊙ O$ 的半径为5，且 $A B = 11$ ，则DE的长度为（）

A、5 B、6 C、 $\sqrt{30}$ D、 $\frac{11}{2}$

查看试题解析
8. 在不透明的袋子中有黑棋子10枚和白棋子若干（它们除颜色外都相同），现随机从中摸出10枚记下颜色后放回，这样连续做了10次，记录了如下的数据：

根据以上数据，估算袋中的白棋子数量为（　　）

A、60枚 B、50枚 C、40枚 D、30枚

查看试题解析
9. 下面有关圆的一些结论：①任意三点确定一个圆；②相等的圆心角所对的弧相等；③平分弦的直径垂直于弦，并且平分弦所对的两条弧；④三角形的外心到三角形三个顶点的距离都相等；⑤任意一个三角形一定有一个外接圆，并且只有一个外接圆．其中错误的结论有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，抛物线 $y = a x^{2} + b x + c$ 与 $x$ 轴交于点A（-1，0），顶点坐标（1，n）与 $y$ 轴的交点在（0，2），（0，3）之间（包含端点），则下列结论：① $3 a + b < 0$ ；② $- 1 \leq a \leq - \frac{2}{3}$ ；③对于任意实数m，a+b≥am²+bm总成立；④关于 $x$ 的方程 $a x^{2} + b x + c = n - 1$ 有两个不相等的实数根.其中结论正确的个数为 $($ 　　 $)$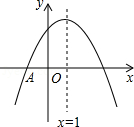

A、1 个 B、2 个 C、3 个 D、4 个

查看试题解析

二、填空题

11. 在平面直角坐标系中，若点A（x+1，2y+1）与点A'（y﹣2，x）关于原点O对称，则代数式x²﹣y²的值为．

查看试题解析
12. 有一个边长为12cm的正六边形，若要剪一张圆形纸片完全盖住这个六边形，则这个圆形纸片的半径最小是cm；

查看试题解析
13. 已知在直角坐标平面内，以点P（1，2）为圆心，r为半径画圆，⊙P与坐标轴恰好有三个交点，那么r的取值是．

查看试题解析
14. 2018﹣2019赛季中国男子篮球职业联赛（CBA），继续采用双循环制（每两队之间都进行两场比赛），总比赛场数为380场．求有多少支队伍参加比赛？设参赛队伍有x支，则可列方程为．

查看试题解析
15. 如图，点B，A，C，D在⊙O上，OA⊥BC，∠AOB=50°，则∠ADC= ．

查看试题解析
16. 将抛物线 $y = a x^{2} + b x + c$ 先向左平移2个单位，再向下平移5个单位，得到抛物线 $y = x^{2} + 4 x - 1$ ，那么原抛物线的解析式是；

查看试题解析
17. 如图，在菱形ABCD中，以AB为直径画弧分别交BC于点F，交对角线AC于点E，若AB=4，F为BC的中点，则图中阴影部分的面积为；

查看试题解析
18. 如图，△ABC是一块绿化带，阴影部分是△ABC的内切圆，将阴影部分修建为花圃，已知AB=15，AC=9，BC=12，一只自由飞翔的小鸟将随机落在这块绿化带上，则小鸟落在花圃上的概率为.

查看试题解析
19. 如图，在平面直角坐标系中，将正方形 $O A B C$ 绕点O逆时针旋转 $45 °$ 后得到正方形 $O A_{1} B_{1} C_{1}$ ，依此方式，绕点O连续旋转2019次得到正方形 $O A_{2019} B_{2019} C_{2019}$ ，如果点A的坐标为（1，0），那么点 $B_{2019}$ 的坐标为．

查看试题解析

三、解答题

20. 解方程

(1)、 $y^{2} - 2 y - 8 = 0$

(2)、 $2 x^{2} - 7 x + 6 = 0$

查看试题解析
21. 如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别是A(﹣3，2)，B(﹣1，4)，C(0，2)．

⑴请画出△ABC关于点O的对称图形△A₁B₁C₁；

⑵将△ABC绕原点O逆时针旋转90°后得到△A₂B₂C₂ ，请画出△A₂B₂C₂并求出在旋转过程中点B所经过的圆弧长．

查看试题解析
22. 有A、B两个黑布袋，A布袋中有四个除标号外完全相同的小球，小球上分别标有数字0，1，2，3，B布袋中有三个除标号外完全相同的小球，小球上分别标有数字0，1，2．小明先从A布袋中随机取出一个小球，用m表示取出的球上标有的数字，再从B布袋中随机取出一个小球，用n表示取出的球上标有的数字．

(1)、若用（m，n）表示小明取球时m与n 的对应值，用列表法(或画树状图)表示出（m，n）的所有取值；

(2)、求关于x的一元二次方程 $x^{2} - m x + \frac{1}{2} n = 0$ 有实数根的概率．

查看试题解析
23. 某服装店在服装销售中发现：进货价每件60元，销售价每件100元的某服装每天可售出20件，为了迎接新春佳节，服装店决定采取适当的促销措施，扩大销售量，增加盈利．经调查发现：如果每件服装降价1元，那么每天就可多售出2件．

(1)、如果服装店想每天销售这种服装盈利1050元，同时又要使顾客得到更多的实惠，那么每件服装应降价多少元？

(2)、每件服装降价多少元时，服装店每天可获得最大利润？最大利润是多少元？

查看试题解析
24. 如图，△ABC内接与⊙O，AB是直径，⊙O的切线PC交BA的延长线于点P，OF∥BC交AC于AC点E，交PC于点F，连接AF.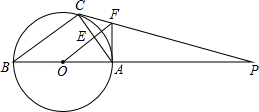

(1)、判断AF与⊙O的位置关系并说明理由；

(2)、若⊙O的半径为4，AF=3，求AC的长.

查看试题解析
25. 如图，点O为Rt△ABC斜边AB上的一点，以OA为半径的⊙O与BC切于点D，与AC交于点E，连接AD.

(1)、求证：AD平分∠BAC；

(2)、若∠BAC=60^∘ ， OA=4，求阴影部分的面积(结果保留π).

查看试题解析
26. 如图1，抛物线y＝﹣x²+mx+n交x轴于点A(﹣2，0)和点B，交y轴于点C(0，2).

(1)、求抛物线的函数表达式；

(2)、若点M在抛物线上，且S_△_AOM＝2S_△_BOC ，求点M的坐标；

(3)、如图2，设点N是线段AC上的一动点，作DN⊥x轴，交抛物线于点D，求线段DN长度的最大值.

查看试题解析