内蒙古自治区呼伦贝尔市扎兰屯市2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2021-08-19 类型：期末考试

进入出卷网下载

一、单选题

1. 关于x的方程（a﹣1）x^|a|+1﹣3x+2＝0是一元二次方程，则（）

A、a≠±1 B、a＝1 C、a＝﹣1 D、a＝±1

查看试题解析
2. 下列图案中既是中心对称图形，又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列说法正确的是（　　）

A、袋中有形状、大小、质地完全一样的5个红球和1个白球，从中随机抽出一个球，一定是红球 B、天气预报“明天降水概率10%”，是指明天有10%的时间会下雨 C、某地发行一种福利彩票，中奖率是千分之一，那么，买这种彩票1000张，一定会中奖 D、连续掷一枚均匀硬币，若5次都是正面朝上，则第六次仍然可能正面朝上

查看试题解析
4. 甲、乙、丙三人站成一排拍照，则甲站在中间的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
5. 关于x的一元二次方程x²﹣mx+（m﹣2）=0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
6. 若抛物线y＝x²﹣3x+c与y轴的交点为（0，2），则下列说法正确的是（　　）

A、抛物线开口向下 B、抛物线与x轴的交点为（﹣1，0），（3，0） C、当x＝1时，y有最大值为0 D、抛物线的对称轴是直线x＝ $\frac{3}{2}$

查看试题解析
7. 两个相似三角形的对应边分别是15cm和23cm，它们的周长相差40cm，则这两个三角形的周长分别是（　　）

A、45cm，85cm B、60cm，100cm C、75cm，115cm D、85cm，125cm

查看试题解析
8. 下列命题正确的是（）

A、圆是轴对称图形，任何一条直径都是它的对称轴 B、平分弦的直径垂直于弦，并且平分弦所对的弧 C、相等的圆心角所对的弧相等，所对的弦相等 D、同弧或等弧所对的圆周角相等

查看试题解析
9.
如图所示，AB是⊙O的直径，点C为⊙O外一点，CA，CD是⊙O的切线，A，D为切点，连接BD，AD．若∠ACD=30°，则∠DBA的大小是（　　）

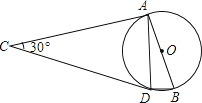A、15° B、30° C、60° D、75°

查看试题解析
10.
如图，在△ABC中，∠B=90°，AB=6cm，BC=12cm，动点P从点A开始沿边AB向B以1cm/s的速度移动（不与点B重合），动点Q从点B开始沿边BC向C以2cm/s的速度移动（不与点C重合）．如果P、Q分别从A、B同时出发，那么经过（　　）秒，四边形APQC的面积最小．

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

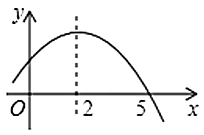
11. 若2是一元二次方程x²+mx﹣4m＝0的一个根，则另一个根是．

查看试题解析
12. 已知点A关于原点的对称点坐标为(﹣1，2)，则点A关于x轴的对称点的坐标为

查看试题解析
13. 在一个不透明的布袋里装有若干个只有颜色不同的红球和白球，其中有3个红球，且从布袋中随机摸出1个球是红球的概率是三分之一，则白球的个数是

查看试题解析
14. 已知圆O的直径为4，点M到圆心O的距离为3，则点M与⊙O的位置关系是．

查看试题解析
15. 如图是二次函数 $y = a x^{2} + b x + c$ 的部分图象，由图象可知不等式 $a x^{2} + b x + c > 0$ 的解集是.

查看试题解析
16. 如图，AB是⊙O的直径，D是⊙O上的任意一点（不与点A、B重合），延长BD到点C，使DC=BD，则△ABC的形状：

查看试题解析
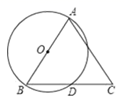17. 如图，已知△ABC，AB=6，AC=5，D是边AB的中点，E是边AC上一点，∠ADE=∠C，∠BAC的平分线分别交DE、BC于点F、G，那么 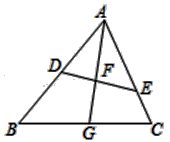$\frac{A F}{A G}$ 的值为．

查看试题解析

三、解答题

18. 解方程： $x^{2} + 2 x - 2 = 0$ .

查看试题解析
19. 有一个直径为1m的圆形铁皮，要从中剪出一个最大的圆心角为90°的扇形ABC，如图所示．

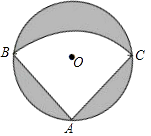(1)、求被剪掉阴影部分的面积：

(2)、用所留的扇形铁皮围成一个圆锥，该圆锥的底面圆的半径是多少？

查看试题解析
20. 如图， $B C$ 是 $⊙ O$ 的弦， $O D ⊥ B C$ 于E，交 $⊙ O$ 于D，若 $B C = 8 ， E D = 2$ ，求 $⊙ O$ 的半径.

查看试题解析
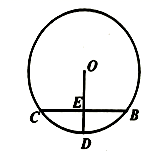21. 如图，有四张背面相同的纸牌A、B、C、D，其正面分别画有四个不同的图形，小明将这四张纸牌背面朝上洗匀后随机摸出一张，放回后洗匀再随机摸出一张．

(1)、用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌用A、B、C、D表示）；

(2)、求两次摸出的牌面图形既是中心对称图形又是轴对称图形的概率．

查看试题解析
22. 如图，ABCD是一块边长为4米的正方形苗圃，园林部门拟将其改造为矩形AEFG的形状，其中点E在AB边上，点G在AD的延长线上，DG = 2BE．设BE的长为x米，改造后苗圃AEFG的面积为y平方米．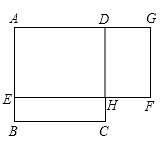

(1)、求y与x之间的函数关系式（不需写自变量的取值范围）；

(2)、根据改造方案，改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等，请问此时BE的长为多少米？

查看试题解析
23. 为了落实国务院的指示精神，地方政府出台了一系列“三农”优惠政策，使农民收入大幅度增加．某农户生产经销一种农产品，已知这种产品的成本价为每千克20元，市场调查发现，该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系： $y = - 2 x + 80$ . 设这种产品每天的销售利润为w元.

(1)、求w与x之间的函数关系式；

(2)、该产品销售价定为每千克多少元时，每天的销售利润最大？最大利润是多少元？

查看试题解析
24. 如图，AB、BC、CD分别与⊙O切于E、F、G，且AB∥CD．连接OB、OC，延长CO交⊙O于点M，过点M作MN∥OB交CD于N．

(1)、求证：MN是⊙O的切线；

(2)、当OB＝6cm，OC＝8cm时，求⊙O的半径及MN的长．

查看试题解析
25. 矩形OABC在直角坐标系中的位置如图所示，A、C两点的坐标分别为A(6，0)、C(0，3)，直线y= $\frac{3}{4}$ x与BC边相交于D．

(1)、求点D的坐标：

(2)、若抛物线y=ax $^{2}$ ＋bx经过D、A两点，试确定此抛物线的表达式：

(3)、P为x轴上方（2）题中的抛物线上一点，求△POA面积的最大值．

查看试题解析