内蒙古自治区呼和浩特市赛罕区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 若关于x的方程 是一元二次方程,则m的取值范围是( )A、 B、 C、 D、2. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、有一个实数根 D、无实数根3. 抛物线 的顶点坐标是( )A、 B、 C、 D、4. 现有两个不透明的袋子,一个装有2个红球、1个白球,另一个装有1个黄球、2个红球,这些球除颜色外完全相同从两个袋子中各随机摸出1个球,摸出的两个球颜色相同的概率是( )A、 B、 C、 D、5. 某林业部门要考察某幼苗的成活率,于是进行了试验,下表中记录了这种幼苗在一定条件下移植的成活情况,则下列说法错误的是( )
移植总数n
400
1500
3500
7000
9000
14000
成活数m
369
1335
3203
6335
8073
12628
成活的频率
0923
0.890
0915
0.905
0.897
0.902
A、由此估计这种幼苗在此条件下成活的概率约为0.9 B、如果在此条件下再移植这种幼苗20000株,则必定成活18000株 C、可以用试验次数累计最多时的频率作为概率的估计值 D、在大量重复试验中,随着试验次数的增加,幼苗成活的频率会越来越稳定,因此可以用频率估计概率6. 如图, 中, ,在同一平面内,将 绕点A旋转到 的位置,使得 ,则 的度数为( ) A、 B、 C、 D、7. 如图,点A,B,C,D,E都在 上,且 的度数为 ,则 等于( )
A、 B、 C、 D、7. 如图,点A,B,C,D,E都在 上,且 的度数为 ,则 等于( ) A、 B、 C、 D、8. 二次函数 与一次函数 在同一坐标系中的大致图象可能是( )A、
A、 B、 C、 D、8. 二次函数 与一次函数 在同一坐标系中的大致图象可能是( )A、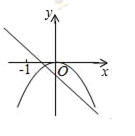 B、
B、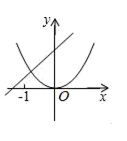 C、
C、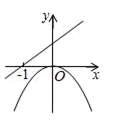 D、
D、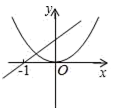 9. 如图,在 的正方形网格中,有三个小正方形已经涂成灰色,若再任意涂灰2个白色小正方形(每个白色小正方形被涂成灰色的可能性相同),使新构成灰色部分的图形是轴对称图形的概率是( )
9. 如图,在 的正方形网格中,有三个小正方形已经涂成灰色,若再任意涂灰2个白色小正方形(每个白色小正方形被涂成灰色的可能性相同),使新构成灰色部分的图形是轴对称图形的概率是( ) A、 B、 C、 D、10. 如图,一次函数y=2x与反比例函数y= (k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为 ,则k的值为( )
A、 B、 C、 D、10. 如图,一次函数y=2x与反比例函数y= (k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为 ,则k的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 地物线 的部分图象如图所示,则当 时,x的取值范围是 .
 12. 如图,点A,B,C都在 上,连接 , , , , , ,则 的大小是 .
12. 如图,点A,B,C都在 上,连接 , , , , , ,则 的大小是 . 13. 如图, 是 的直径, 是 的切线, 交 于点C, , ,则 .
13. 如图, 是 的直径, 是 的切线, 交 于点C, , ,则 . 14. 如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y= (x<0)的图象经过点A,若S△AOB= ,则k的值为.
14. 如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y= (x<0)的图象经过点A,若S△AOB= ,则k的值为.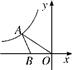 15. 如图,在菱形ABCD中,对角线AC,BD交于点O,∠ABC=60°,AB=2,分别以点A、点C为圆心,以AO的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为.(结果保留π)
15. 如图,在菱形ABCD中,对角线AC,BD交于点O,∠ABC=60°,AB=2,分别以点A、点C为圆心,以AO的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为.(结果保留π)
16. 如图,直线 与抛物线 交于A,B两点,点P是y轴上的一个动点,当 的周长最小时, .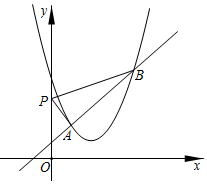
三、解答题
-
17. 解方程:(1)、 ;(2)、 .18. 如图,某小区规划在一个长 ,宽 的矩形场地上,修建两横两竖四条同样宽的道路,且横、竖道路分别与矩形的长、宽平行,其余部分种草坪,若使每块草坪的面积都为 .应如何设计道路的宽度?
 19. 如图,把点 以原点为中心,分别逆时针旋转 , , ,得到点B,C,D.
19. 如图,把点 以原点为中心,分别逆时针旋转 , , ,得到点B,C,D. (1)、画出旋转后的图形,写出点B,C,D的坐标,并顺次连接A、B,C,D各点;(2)、求出四边形 的面积;(3)、结合(1),若把点 绕原点逆时针旋转 到点 ,则点 的坐标是什么?20. 已知: 中, .(1)、求作: 的外接圆;(要求:尺规作图,保留作图痕迹,不写作法)
(1)、画出旋转后的图形,写出点B,C,D的坐标,并顺次连接A、B,C,D各点;(2)、求出四边形 的面积;(3)、结合(1),若把点 绕原点逆时针旋转 到点 ,则点 的坐标是什么?20. 已知: 中, .(1)、求作: 的外接圆;(要求:尺规作图,保留作图痕迹,不写作法)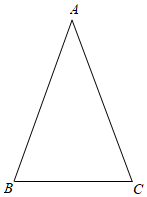 (2)、若 的外接圆的圆心O到BC边的距离为4,BC=12,求 的面积.21. 在一个不透明的盒子中装有4张卡片.4张卡片的正面分别标有数字1,2,3,4,这些卡片除数字外都相同,将卡片搅匀.(1)、从盒子任意抽取一张卡片,恰好抽到标有奇数卡片的概率是:;(2)、先从盒子中任意抽取一张卡片,再从余下的3张卡片中任意抽取一张卡片,求抽取的2张卡片标有数字之和大于4的概率(请用画树状图或列表等方法求解).22. 汛期到来,山洪暴发.下表记录了某水库 内水位的变化情况,其中 表示时间(单位: ), 表示水位高度(单位: ),当 时,达到警戒水位,开始开闸放水.
(2)、若 的外接圆的圆心O到BC边的距离为4,BC=12,求 的面积.21. 在一个不透明的盒子中装有4张卡片.4张卡片的正面分别标有数字1,2,3,4,这些卡片除数字外都相同,将卡片搅匀.(1)、从盒子任意抽取一张卡片,恰好抽到标有奇数卡片的概率是:;(2)、先从盒子中任意抽取一张卡片,再从余下的3张卡片中任意抽取一张卡片,求抽取的2张卡片标有数字之和大于4的概率(请用画树状图或列表等方法求解).22. 汛期到来,山洪暴发.下表记录了某水库 内水位的变化情况,其中 表示时间(单位: ), 表示水位高度(单位: ),当 时,达到警戒水位,开始开闸放水.0
2
4
6
8
10
12
14
16
18
20
14
15
16
17
18
14.4
12
10.3
9
8
7.2
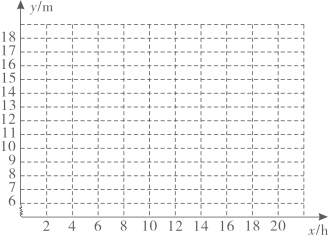 (1)、在给出的平面直角坐标系中,根据表格中的数据描出相应的点.(2)、请分别求出开闸放水前和放水后最符合表中数据的函数解析式.(3)、据估计,开闸放水后,水位的这种变化规律还会持续一段时间,预测何时水位达到 .23. 一名大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价为24元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于32元件,市场调查发现,该产品每天的销售最y(件)与x(元/件)之间的函数关系如图所示.
(1)、在给出的平面直角坐标系中,根据表格中的数据描出相应的点.(2)、请分别求出开闸放水前和放水后最符合表中数据的函数解析式.(3)、据估计,开闸放水后,水位的这种变化规律还会持续一段时间,预测何时水位达到 .23. 一名大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价为24元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于32元件,市场调查发现,该产品每天的销售最y(件)与x(元/件)之间的函数关系如图所示. (1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、求每天的销售利润W(元)与销售单价x(元/件)之间的函数关系式并求出每天销售价为多少元时,每天的销售利润最大?最大利润是多少?24. 如图,在 中, , ,点 在 的内部, 经过 , 两点,交 于点 ,连接 并延长交 于点 ,以 , 为邻边作 .
(1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、求每天的销售利润W(元)与销售单价x(元/件)之间的函数关系式并求出每天销售价为多少元时,每天的销售利润最大?最大利润是多少?24. 如图,在 中, , ,点 在 的内部, 经过 , 两点,交 于点 ,连接 并延长交 于点 ,以 , 为邻边作 . (1)、判断 与 的位置关系,并说明理由.(2)、若点 是 的中点, 的半径为2,求 的长.25. 如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0)两点,与y轴交于点C , 点D是抛物线上一个动点,设点D的横坐标为m(1<m<4)连接BC , DB , DC .
(1)、判断 与 的位置关系,并说明理由.(2)、若点 是 的中点, 的半径为2,求 的长.25. 如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0)两点,与y轴交于点C , 点D是抛物线上一个动点,设点D的横坐标为m(1<m<4)连接BC , DB , DC . (1)、求抛物线的函数解析式;(2)、△BCD的面积是否存在最大值,若存在,求此时点D的坐标;若不存在,说明理由;(3)、在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M , 使得以点B , D , M , N为顶点的四边形是平行四边形.若存在,请直接写出点M的坐标;若不存在,请说明理由.
(1)、求抛物线的函数解析式;(2)、△BCD的面积是否存在最大值,若存在,求此时点D的坐标;若不存在,说明理由;(3)、在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M , 使得以点B , D , M , N为顶点的四边形是平行四边形.若存在,请直接写出点M的坐标;若不存在,请说明理由.