内蒙古自治区赤峰市林西县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 下列图形中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知关于x的一元二次方程 有两个实数根,则k的取值范围是( )A、 B、 且 C、 且 D、3. 方程 是关于x的一元二次方程,则m的值是( )A、 B、 C、 D、不存在4. 常胜村2017年的人均收入为12000元,2019年的人均收入为15000元,求人均收入的年增长率.若设人均收入的年增长率为x,根据题意列方程为( )A、 B、 C、 D、5. 抛物线 的顶点坐标是( )A、(2,9) B、(2,-9) C、(-2,9) D、(-2,-9)6. 在同一直角坐标系中,二次函数 与一次函数 的大致图象可能( )A、
2. 已知关于x的一元二次方程 有两个实数根,则k的取值范围是( )A、 B、 且 C、 且 D、3. 方程 是关于x的一元二次方程,则m的值是( )A、 B、 C、 D、不存在4. 常胜村2017年的人均收入为12000元,2019年的人均收入为15000元,求人均收入的年增长率.若设人均收入的年增长率为x,根据题意列方程为( )A、 B、 C、 D、5. 抛物线 的顶点坐标是( )A、(2,9) B、(2,-9) C、(-2,9) D、(-2,-9)6. 在同一直角坐标系中,二次函数 与一次函数 的大致图象可能( )A、 B、
B、 C、
C、 D、
D、 7. 若二次函数 的图象如图,与x轴的一个交点为(1,0),则下列各式中不成立的是( )
7. 若二次函数 的图象如图,与x轴的一个交点为(1,0),则下列各式中不成立的是( ) A、 B、 C、 D、8. 下列说法正确的是( )A、垂直于半径的直线是圆的切线 B、经过三点一定可以作圆 C、平分弦的直径垂直于弦 D、每个三角形都有一个外接圆9. 抛物线 的部分图象如图所示,当 时,x的取值范围是( )
A、 B、 C、 D、8. 下列说法正确的是( )A、垂直于半径的直线是圆的切线 B、经过三点一定可以作圆 C、平分弦的直径垂直于弦 D、每个三角形都有一个外接圆9. 抛物线 的部分图象如图所示,当 时,x的取值范围是( ) A、x>2 或x<-3 B、-3<x<2 C、x>2或x<-4 D、-4<x<210. ⊙O的半径为15cm,AB,CD是⊙O的两条弦,AB∥CD,AB=24cm,CD=18cm,则AB和CD之间的距离是( )A、21cm B、3cm C、17cm或7cm D、21cm或3cm11. 如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是( )
A、x>2 或x<-3 B、-3<x<2 C、x>2或x<-4 D、-4<x<210. ⊙O的半径为15cm,AB,CD是⊙O的两条弦,AB∥CD,AB=24cm,CD=18cm,则AB和CD之间的距离是( )A、21cm B、3cm C、17cm或7cm D、21cm或3cm11. 如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是( )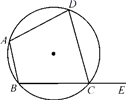 A、115° B、105° C、100° D、95°12. 如图,直角△ABC 中, , , ,以 A为圆心,AC 长为半径画四分之一圆,则图中阴影部分的面积是( )
A、115° B、105° C、100° D、95°12. 如图,直角△ABC 中, , , ,以 A为圆心,AC 长为半径画四分之一圆,则图中阴影部分的面积是( ) A、 B、 C、 D、13. 如图,PA , PB是⊙O的切线,A , B为切点,AC是⊙O的直径,∠BAC=28°,则∠P的度数是( )
A、 B、 C、 D、13. 如图,PA , PB是⊙O的切线,A , B为切点,AC是⊙O的直径,∠BAC=28°,则∠P的度数是( ) A、50° B、58° C、56° D、55°14. 如图,ABCD是矩形纸片,翻折∠B,∠D,使AD,BC边与对角线AC重叠,且顶点B,D恰好落在同一点O上,折痕分别是CE,AF,则等于( )
A、50° B、58° C、56° D、55°14. 如图,ABCD是矩形纸片,翻折∠B,∠D,使AD,BC边与对角线AC重叠,且顶点B,D恰好落在同一点O上,折痕分别是CE,AF,则等于( )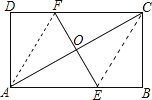 A、 B、2 C、1.5 D、
A、 B、2 C、1.5 D、二、填空题
-
15. 方程 的根是 .16. 如图,△ABC是直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,恰好能与△ACP′完全重合,如果AP=8,则PP′的长度为 .
 17. 用一个圆心角为150°,半径为8的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为 .18. 如图是一个三角形点阵,从上向下数有无数多行,其中第一行有2个点,第二行有4个点……第n行有2n个点……,若前n行的点数和为930,则n是 .
17. 用一个圆心角为150°,半径为8的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为 .18. 如图是一个三角形点阵,从上向下数有无数多行,其中第一行有2个点,第二行有4个点……第n行有2n个点……,若前n行的点数和为930,则n是 .
三、解答题
-
19. 在下列网格中,每个小正方形的边长均为1个单位,△ABC在网格中的位置如图所示:

⑴在图中画出△ABC先向右平移2个单位,再向上平移3个单位后的图形 ;
⑵若点A的坐标是(-4,-3),试在图中画出平面直角坐标系,坐标系的原点记作O;
⑶根据⑵的坐标系,作出 以O为旋转中心,逆时针旋转90º后的图形 ,并求出点A一共运动的路径长.
20. 阅读理解,我们已经学习了点和圆、直线和圆的位置关系以及各种位置关系的数量表示,如下表:
类似于研究点和圆、直线和圆的位置关系,我们也可以用两圆的半径和两圆的圆心距(两圆圆心的距离)来刻画两圆的位置关系.如果两圆的半径分别为 和 (r1>r2),圆心距为d,请你通过画图,并利用d与 和 之间的数量关系探索两圆的位置关系.
图形表示
(圆和圆的位置关系)
数量表示
(圆心距d与两圆的半径 、 的数量关系)
21. 如图,AB为⊙O的直径,AC是弦,D为线段AB延长线上一点,过C,D作射线DP,若∠D=2∠CAD=45°. (1)、证明:DP是⊙O的切线.(2)、若CD=3,求BD的长.22. 在菱形 ABCD 中, ∠ABC=60°,点 P 是射线 BD 上一动点,以 AP 为边向右侧作等边 △APE ,点 E 的位置随点 P 的位置变化而变化.
(1)、证明:DP是⊙O的切线.(2)、若CD=3,求BD的长.22. 在菱形 ABCD 中, ∠ABC=60°,点 P 是射线 BD 上一动点,以 AP 为边向右侧作等边 △APE ,点 E 的位置随点 P 的位置变化而变化.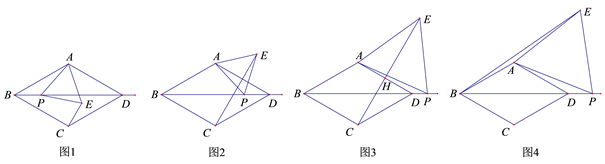 (1)、如图1,当点 E 在菱形ABCD内部或边上时,连接CE , BP 与 CE 的数量关系是 , CE 与 AD 的位置关系是;
(1)、如图1,当点 E 在菱形ABCD内部或边上时,连接CE , BP 与 CE 的数量关系是 , CE 与 AD 的位置关系是;
(2)、当点 E 在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3)、如图4,当点 P 在线段 BD 的延长线上时,连接 BE ,若 , , 求四边形 ADPE 的面积.
23. 甲、乙、丙三个球迷决定通过抓阄来决定谁得到仅有的一张球票.他们准备了三张纸片,其中一张上画了个五星,另两张空白,团成外观一致的三个纸团.抓中画有五角星纸片的人才能得到球票.刚要抓阄,甲问:“谁先抓?先抓的人会不会抓中的机会比别人大?”你认为他的怀疑有没有道理?谈谈你的想法并用列表或画树状图方法说明原因.24. 如图,直线 与x轴交于点A , 与y轴交于点B , 抛物线y=-x2+bx+c经过A , B两点. (1)、求抛物线的解析式.(2)、点P是第一象限抛物线上的一点,连接PA , PB , PO , 若△POA的面积是△POB面积的 倍.
(1)、求抛物线的解析式.(2)、点P是第一象限抛物线上的一点,连接PA , PB , PO , 若△POA的面积是△POB面积的 倍.①求点P的坐标;
②点Q为抛物线对称轴上一点,请求出QP+QA的最小值.