内蒙古自治区包头市青山区22019-2020学年九年级上学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 计算 的值是( )A、 B、 C、 D、2. 在下列四个函数中,当 时,y随x的增大而减小的函数是( )A、 B、 C、 D、3. 如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为 ,缆车速度为每分钟40米,从山脚下A到达山顶B缆车需要15分钟,则山的高度 为( )米.
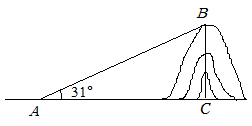 A、 B、 C、 D、4. 两名同学在一次用频率估计概率的试验中统计了某一结果出现的频率,绘制出统计图如图所示,则符合这一结果的试验可能是( )
A、 B、 C、 D、4. 两名同学在一次用频率估计概率的试验中统计了某一结果出现的频率,绘制出统计图如图所示,则符合这一结果的试验可能是( )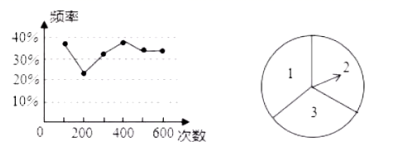 A、抛一枚硬币,正面朝上的概率 B、掷一枚正六面体的骰子,出现 点的概率 C、转动如图所示的转盘,转到数字为奇数的概率 D、从装有 个红球和 个蓝球的口袋中任取一个球恰好是蓝球的概率5. 一个圆柱的三视图如图所示,若其俯视图为圆,则这个圆柱的体积为( )
A、抛一枚硬币,正面朝上的概率 B、掷一枚正六面体的骰子,出现 点的概率 C、转动如图所示的转盘,转到数字为奇数的概率 D、从装有 个红球和 个蓝球的口袋中任取一个球恰好是蓝球的概率5. 一个圆柱的三视图如图所示,若其俯视图为圆,则这个圆柱的体积为( )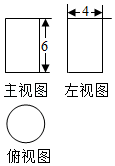 A、 B、 C、 D、6. 将抛物线y=x2先向上平移1个单位,再向左平移2个单位,则新的函数解析式为( ).A、 B、 C、 D、7. 如图,△ABC内接于圆,D是BC上一点,将∠B沿AD翻折,B点正好落在圆点E处,若∠C=50°,则∠BAE的度数是( )
A、 B、 C、 D、6. 将抛物线y=x2先向上平移1个单位,再向左平移2个单位,则新的函数解析式为( ).A、 B、 C、 D、7. 如图,△ABC内接于圆,D是BC上一点,将∠B沿AD翻折,B点正好落在圆点E处,若∠C=50°,则∠BAE的度数是( )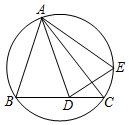 A、40° B、50° C、80° D、90°8. 从﹣1,0,1,2,3这五个数中,任意选一个数记为m , 能使关于x的不等式组 有解,并且使一元二次方程(m﹣1)x2+2mx+m+2=0有实数根的数m的个数为( )A、1个 B、2个 C、3个 D、4个9. 如图,一张矩形纸片ABCD的长BC=xcm , 宽AB=ycm , 以宽AB为边剪去一个最大的正方形ABEF , 若剩下的矩形ECDF与原矩形ABCD相似,则 的值为( )
A、40° B、50° C、80° D、90°8. 从﹣1,0,1,2,3这五个数中,任意选一个数记为m , 能使关于x的不等式组 有解,并且使一元二次方程(m﹣1)x2+2mx+m+2=0有实数根的数m的个数为( )A、1个 B、2个 C、3个 D、4个9. 如图,一张矩形纸片ABCD的长BC=xcm , 宽AB=ycm , 以宽AB为边剪去一个最大的正方形ABEF , 若剩下的矩形ECDF与原矩形ABCD相似,则 的值为( )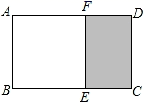 A、 B、 C、 D、10. 若点 在反比例函数 的图象上,且 ,则下列各式正确的是( )A、 B、 C、 D、11. 已知下列命题:
A、 B、 C、 D、10. 若点 在反比例函数 的图象上,且 ,则下列各式正确的是( )A、 B、 C、 D、11. 已知下列命题:①若 ,则 ;
②当 时,若 ,则 ;
③直角三角形中斜边上的中线等于斜边的一半;
④矩形的两条对角线相等.
其中原命题与逆命题均为真命题的个数是( )
A、 个 B、 个 C、 个 D、 个12. 如图,抛物线y=ax2+bx+c的对称轴为x=﹣1,且过点( ,0),有下列结论:①abc>0; ②a﹣2b+4c>0;③25a﹣10b+4c=0;④3b+2c>0;其中所有正确的结论是( )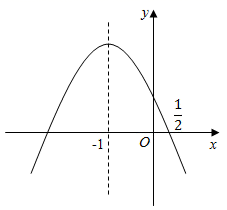 A、①③ B、①③④ C、①②③ D、①②③④
A、①③ B、①③④ C、①②③ D、①②③④二、填空题
-
13. 方程x2=2的解是 .
14. 从﹣2,﹣1,1,2四个数中,随机抽取两个数相乘,积为大于﹣4小于2的概率是 .
15. 已知一个菱形的边长为2,较长的对角线长为2 ,则这个菱形的面积是 .16. 如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为米(结果保留根号).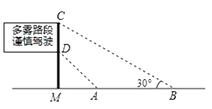 17. 用一根长为32cm的铁丝围成一个矩形,则围成矩形面积的最大值是 cm2 .18. 如图,在 中, ,且 , ,点 是斜边 上的一个动点,过点 分别作 于点 , 于点 ,连接 ,则线段 的最小值为 .
17. 用一根长为32cm的铁丝围成一个矩形,则围成矩形面积的最大值是 cm2 .18. 如图,在 中, ,且 , ,点 是斜边 上的一个动点,过点 分别作 于点 , 于点 ,连接 ,则线段 的最小值为 .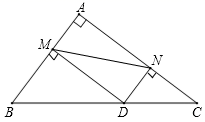 19. 如图,一次函数与反比例函数的图象分别是直线 和双曲线.直线 与双曲线的一个交点为点 轴于点 ,则此反比例函数的解析式为.
19. 如图,一次函数与反比例函数的图象分别是直线 和双曲线.直线 与双曲线的一个交点为点 轴于点 ,则此反比例函数的解析式为. 20. 如图,在矩形 中,点E为 的中点, 交 于点F,连接 ,下列结论:
20. 如图,在矩形 中,点E为 的中点, 交 于点F,连接 ,下列结论: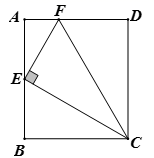
① ;
② ;
③ ;
④若 ,则 .
其中正确的结论是.(填写所有正确结论的序号)
三、解答题
-
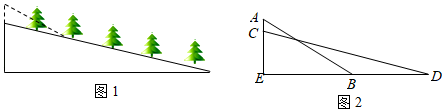
21. 2018年高一新生开始,某省全面启动高考综合改革,实行“3+1+2”的高考选考方案.“3”是指语文、数学、外语三科必考;“1”是指从物理、历史两科中任选一科参加选考,“2”是指从政治、化学、地理、生物四科中任选两科参加选考(1)、“1+2”的选考方案共有多少种?请直接写出所有可能的选法;(选法与顺序无关,例如:“物、政、化”与“物、化、政”属于同一种选法)(2)、高一学生小明和小杰将参加新高考,他们酷爱历史和生物,两人约定必选历史和生物.他们还需要从政治、化学、地理三科中选一科参考,若这三科被选中的机会均等,请用列表或画树状图的方法,求出他们恰好都选中政治的概率.22. 自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图1所示的坡路进行改造.如图2所示,改造前的斜坡 米,坡度为 ;将斜坡 的高度 降低 米后,斜坡 改造为斜坡 ,其坡度为 .求斜坡 的长.(结果保留根号)
 23. 2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
23. 2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.月份x
…
3
4
5
6
…
售价y1/元
…
12
14
16
18
…
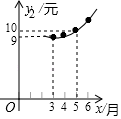 (1)、求y1与x之间的函数关系式.(2)、求y2与x之间的函数关系式.(3)、设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?24. 如图,已知AB是⊙O的直径,AC为弦,且平分∠BAD,AD⊥CD,垂足为D.
(1)、求y1与x之间的函数关系式.(2)、求y2与x之间的函数关系式.(3)、设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?24. 如图,已知AB是⊙O的直径,AC为弦,且平分∠BAD,AD⊥CD,垂足为D.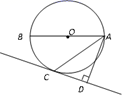 (1)、求证:CD是⊙O的切线;(2)、若⊙O的直径为4,AD=3,试求∠BAC的度数.25. 探究问题:(1)、方法感悟:
(1)、求证:CD是⊙O的切线;(2)、若⊙O的直径为4,AD=3,试求∠BAC的度数.25. 探究问题:(1)、方法感悟:如图①,
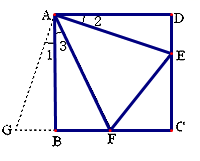
在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45°
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2,
∴∠1+∠3=45°.
即∠GAF=∠ .
又AG=AE,AF=AF
∴△GAF≌ .
∴=EF,故DE+BF=EF.
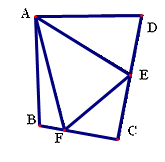
(2)、方法迁移:如图②,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF= ∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
 (3)、问题拓展:
(3)、问题拓展:如图③,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足∠EAF= ∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由)
.
 26. 如图,对称轴是 的抛物线 与x轴交于 两点,与y轴交于点 ,
26. 如图,对称轴是 的抛物线 与x轴交于 两点,与y轴交于点 , (1)、求抛物线的函数表达式;(2)、若点P是直线 下方的抛物线上的动点,求 的面积的最大值;(3)、若点P在抛物线对称轴左侧的抛物线上运动,过点P作 铀于点D,交直线 于点E,且 ,求点P的坐标;(4)、在对称轴上是否存在一点M,使 的周长最小,若存在,请求出M点的坐标和 周长的最小值;若不存在,请说明理由.
(1)、求抛物线的函数表达式;(2)、若点P是直线 下方的抛物线上的动点,求 的面积的最大值;(3)、若点P在抛物线对称轴左侧的抛物线上运动,过点P作 铀于点D,交直线 于点E,且 ,求点P的坐标;(4)、在对称轴上是否存在一点M,使 的周长最小,若存在,请求出M点的坐标和 周长的最小值;若不存在,请说明理由.