内蒙古乌海市海勃湾区2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2021-08-19 类型：期末考试

进入出卷网下载

一、单选题

1. 计算 ${(\frac{1}{3})}^{- 2}$ 的结果是（）

A、 $- \frac{1}{9}$ B、 $\frac{1}{9}$ C、 $- \frac{1}{6}$ D、9

查看试题解析
2. 式子 $\frac{x}{\sqrt{x} - 2}$ 有意义的x的取值范围（）

A、x ≥4 B、x≥2 C、x≥0且x≠4 D、x≥0且x≠2

查看试题解析
3. 一次抽奖活动特等奖的中奖率为 $\frac{1}{50000}$ ,把 $\frac{1}{50000}$ 用科学记数法表示为（　　）

A、 $5 \times 10^{﹣ 4}$ B、 $5 \times 10^{﹣ 5}$ C、 $2 \times 10^{﹣ 4}$ D、 $2 \times 10^{﹣ 5}$

查看试题解析
4. 下列计算正确的是（）

A、 $a^{2} + a^{2} = a^{4}$ B、 ${(a + b)}^{2} = a^{2} + b^{2}$ C、 ${(a^{3})}^{3} = a^{9}$ D、 $a^{3} \cdot a^{2} = a^{6}$

查看试题解析
5. 点点同学对数据25,43,28,2□,43,36,52进行统计分析，发现其中一个两位数的个位数被墨水涂污看不到了，则计算结果与涂污数字无关的是（）

A、平均数 B、中位数 C、方差 D、众数

查看试题解析
6. 若不等式组 ${\begin{array}{l} \frac{x + 1}{3} < \frac{x}{2} - 1 \\ x < 4 m \end{array}$ 无解，则 $m$ 的取值范围为（）

A、 $m \leq 2$ B、 $m < 2$ C、 $m \geq 2$ D、 $m > 2$

查看试题解析
7. 一元二次方程 $x^{2} - 3 x + 1 = 0$ 的两个根为 $x_{1} ， x_{2}$ ，则 $x_{1}^{2} + 3 x_{2} + x_{1} x_{2} - 2$ 的值是（）

A、10 B、9 C、8 D、7

查看试题解析
8. 直径为1个单位长度的圆上有一点A与数轴上表示1的点重合，圆沿着数轴向左滚动一周，点A与数轴上的点B重合，则B表示的实数是（）

A、 $2 π - 1$ B、 $π - 1$ C、 $1 - π$ D、 $1 - 2 π$

查看试题解析
9. 如图，在△ABC中，∠C= $90^{°}$ ，∠B= $30^{°}$ ，以点A为圆心，适当长为半径画弧，分别交AB，AC于点M、N，再分别以点M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于P，作射线AP交BC于点D，下列说法错误的是（）

A、∠ADC= $60^{°}$ B、AD=BD C、 $S_{△ A C D} ： S_{△ A B D} = 1 ： 3$ D、CD= $\frac{1}{2}$ BD

查看试题解析
10. 如图，在⊙O中，∠BAC＝15°，∠ADC＝20°，则∠ABO的度数为（）

A、70° B、55° C、45° D、35°

查看试题解析
11. 下列命题①若 $a > b$ ，则 $a m^{2} > b m^{2}$ ②相等的圆心角所对的弧相等③各边都相等的多边形是正多边形 ④ $\sqrt{16}$ 的平方根是 $\pm 4$ ．其中真命题的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
12. 已知二次函数y＝ax²+bx+c（a≠0）的图象如图所示，有下列5个结论：
①abc＞0；②b＜a+c；③4a+2b+c＞0；④2c＜3b；⑤a+b＞m（am+b）（m≠1的实数）.

其中正确的结论有（　　）

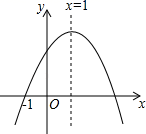A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

13. 计算 $\frac{a^{2}}{a - 1} - a - 1$ 的结果是.

查看试题解析
14. 已知x-2y=3，试求9-4x+8y=

查看试题解析
15. 如图示一些小正方体木块所搭的几何体，从正面和从左面看到的图形，则搭建该几何体最多需要块正方体木块.

查看试题解析
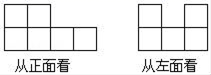16. ▱ABCD的两条对角线AC、BD相交于O，现从下列条件：①AC⊥BD②AB=BC③AC=BD ④∠ABD=∠CBD中随机取一个作为条件，可推出▱ABCD是菱形的概率是

查看试题解析
17. 如图，以AB为直径，点O为圆心的半圆经过点C，若AC=BC= $\sqrt{2}$ ，则图中阴影部分的面积是．

查看试题解析
18. 在平面直角坐标系xOy中，点O的坐标为O，▱OABC的顶点A在反比例函数 $y = \frac{2}{x}$ 的图象上，顶点B在反比例函数 $y = \frac{5}{x}$ 的图象上，点C在x轴正半轴上，则▱OABC的面积是

查看试题解析
19. 如图，在矩形ABCD中，AB=6，BC=4，M是AD的中点，N是AB边上的动点，将△AMN沿MN所在直线折叠，得到△ $A^{'}MN$ ，连接 $A^{'}C$ ，则 $A^{'}C$ 的最小值是

查看试题解析
20. 如图，在正方形ABCD中，AB=4，点M在CD的边上，且DM=1，ΔAEM与ΔADM关于AM所在的直线对称，将ΔADM按顺时针方向绕点A旋转90°得到ΔABF，连接EF，则线段EF的长为

查看试题解析

三、解答题

21. 小敏为了解本市的空气质量情况，从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计，绘制了如图所示的条形统计图和扇形统计图（部分信息未给出）．

请你根据图中提供的信息，解答下列问题：

(1)、计算被抽取的天数；

(2)、请补全条形统计图，并求扇形统计图中表示优的扇形的圆心角度数；

(3)、请估计该市这一年（365天）达到优和良的总天数．

查看试题解析
22. 学校要在教学楼侧面悬挂中考励志的标语牌，如图所示，为了使标语牌醒目，计划设计标语牌的宽度为BC，为了测量BC，在距教学楼20米的升旗台P处利用测角仪测得教学楼AB的顶端点B的仰角为 $60^{°}$ ，点C的仰角为 $45^{°}$ ，求标语牌BC的宽度（结果保留根号）

查看试题解析
23. 如图，要在长、宽分别为40米、24米的矩形赏鱼池内建一个正方形的亲水平台．为了方便行人观赏，分别从东、南、西、北四个方向修四条等宽的小路与平台相连，若小路的宽是正方形平台边长的 $\frac{1}{4}$ ，小路与亲水平台的面积之和占矩形赏鱼池面积的 $\frac{1}{6}$ ，求小路的宽．

查看试题解析
24. 如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD于点E，DA平分∠BDE

(1)、求证：AE是⊙O的切线；

(2)、若∠DBC=30°，DE=1 cm，求BD的长．

查看试题解析
25. 如图1，点E是正方形ABCD边CD上任意一点，以DE为边作正方形DEFG，连接BF，点M是线段BF中点，射线EM与BC交于点H，连接CM．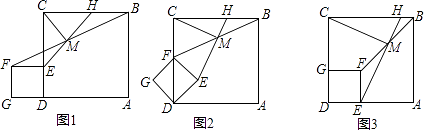

(1)、请直接写出CM和EM的数量关系和位置关系；

(2)、把图1中的正方形DEFG绕点D顺时针旋转45°，此时点F恰好落在线段CD上，如图2，其他条件不变，（1）中的结论是否成立，请说明理由；

(3)、把图1中的正方形DEFG绕点D顺时针旋转90°，此时点E、G恰好分别落在线段AD、CD上，如图3，其他条件不变，（1）中的结论是否成立，请说明理由．

查看试题解析
26. 综合与探究
如图，抛物线 $y = a x^{2} + b x + 6$ 经过点A(-2，0)，B(4，0)两点，与 $y$ 轴交于点C，点D是抛物线上一个动点，设点D的横坐标为 $m (1 < m < 4)$ .连接AC，BC，DB，DC.

(1)、求抛物线的函数表达式；

(2)、△BCD的面积等于△AOC的面积的 $\frac{3}{4}$ 时，求 $m$ 的值；

(3)、在(2)的条件下，若点M是 $x$ 轴上的一个动点，点N是抛物线上一动点，试判断是否存在这样的点M，使得以点B，D，M，N为顶点的四边形是平行四边形，若存在，请直接写出点M的坐标；若不存在，请说明理由.

查看试题解析