内蒙古自治区包头市2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 下列函数属于二次函数的是A、 B、 C、 D、2. 下列一元二次方程中,没有实数根的是( ).A、 B、 C、 D、3. 下列四个图形中,既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 我市组织学生开展志愿者服务活动,小晴和小霞从“图书馆,博物馆,科技馆”三个场馆中随机选择一个参加活动,两人恰好选择同一场馆的概率是( )A、 B、 C、 D、5. 如图, 是 的直径, , 是 上的两点,且 平分 , 分别与 , 相交于点 , ,则下列结论不一定成立的是( )
4. 我市组织学生开展志愿者服务活动,小晴和小霞从“图书馆,博物馆,科技馆”三个场馆中随机选择一个参加活动,两人恰好选择同一场馆的概率是( )A、 B、 C、 D、5. 如图, 是 的直径, , 是 上的两点,且 平分 , 分别与 , 相交于点 , ,则下列结论不一定成立的是( )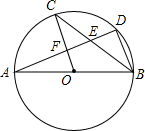 A、 B、 C、 D、6. 函数 与 ( )在同一坐标系中的图象可能是( )A、
A、 B、 C、 D、6. 函数 与 ( )在同一坐标系中的图象可能是( )A、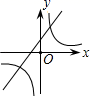 B、
B、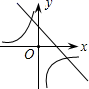 C、
C、 D、
D、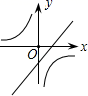 7. 某校“研学”活动小组在一次野外实践时,发现一种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是 ,则这种植物每个支干长出的小分支个数是( )A、 B、 C、 D、8. 如图,点A , B , C , D在⊙O上,AB=AC , ∠A=40°,CD∥AB , 若⊙O的半径为2,则图中阴影部分的面积是( )
7. 某校“研学”活动小组在一次野外实践时,发现一种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是 ,则这种植物每个支干长出的小分支个数是( )A、 B、 C、 D、8. 如图,点A , B , C , D在⊙O上,AB=AC , ∠A=40°,CD∥AB , 若⊙O的半径为2,则图中阴影部分的面积是( )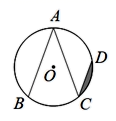 A、 B、 C、 D、9. 如图,是二次函数 图象的一部分,在下列结论中:① ;② ;③ 有两个相等的实数根;④ ;其中正确的结论有( )
A、 B、 C、 D、9. 如图,是二次函数 图象的一部分,在下列结论中:① ;② ;③ 有两个相等的实数根;④ ;其中正确的结论有( ) A、1个 B、2 个 C、3 个 D、4个10. 如图, , 、 ,…是分别以 、 、 ,…为直角顶点,一条直角边在 轴正半轴上的等腰直角三角形,其斜边的中点 , , ,…均在反比例函数 ( )的图象上.则 的值为( )
A、1个 B、2 个 C、3 个 D、4个10. 如图, , 、 ,…是分别以 、 、 ,…为直角顶点,一条直角边在 轴正半轴上的等腰直角三角形,其斜边的中点 , , ,…均在反比例函数 ( )的图象上.则 的值为( ) A、 B、6 C、 D、
A、 B、6 C、 D、二、填空题
-
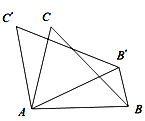
11. 不透明袋子中有2个红球和4个蓝球,这些球除颜色外无其他差别,从袋子中随机取出1个球是红球的概率是.12. 在某市中考体考前,某初三学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为 ,由此可知该生此次实心球训练的成绩为米.13. 一个圆锥的侧面展开图是半径为8的半圆,则该圆锥的全面积是.14. 如图,在△ABC中,∠BAC=75°,以点A为旋转中心,将△ABC绕点A逆时针旋转,得△AB'C' , 连接BB' , 若BB'∥AC' , 则∠BAC′ 的度数是.
 15. 如图,直线 交x轴于点A , 交y轴于点B , 点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P , 当⊙P与直线AB相切时,点P的横坐标是
15. 如图,直线 交x轴于点A , 交y轴于点B , 点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P , 当⊙P与直线AB相切时,点P的横坐标是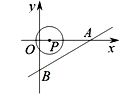 16. 如图,直线 与抛物线 交于A,B两点,点P是y轴上的一个动点,当 的周长最小时, .
16. 如图,直线 与抛物线 交于A,B两点,点P是y轴上的一个动点,当 的周长最小时, .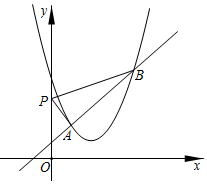
三、解答题
-
17. 解方程:(1)、(2)、18. 2019年4月23日是第二十四个“世界读书日“.某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:
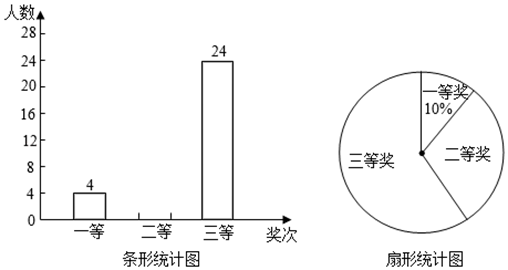 (1)、求本次比赛获奖的总人数,并补全条形统计图;(2)、求扇形统计图中“二等奖”所对应扇形的圆心角度数;(3)、学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.19. 如图,菱形ABCD的顶点A , D在直线l上,∠BAD=60°,以点A为旋转中心将菱形ABCD顺时针旋转α(0°<α<30°),得到菱形AB′C′D′ , B′C′交对角线AC于点M , C′D′交直线l于点N , 连接MN , 当MN∥B′D′ 时,解答下列问题:
(1)、求本次比赛获奖的总人数,并补全条形统计图;(2)、求扇形统计图中“二等奖”所对应扇形的圆心角度数;(3)、学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.19. 如图,菱形ABCD的顶点A , D在直线l上,∠BAD=60°,以点A为旋转中心将菱形ABCD顺时针旋转α(0°<α<30°),得到菱形AB′C′D′ , B′C′交对角线AC于点M , C′D′交直线l于点N , 连接MN , 当MN∥B′D′ 时,解答下列问题: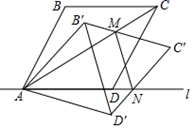 (1)、求证:△AB′M≌△AD′N;(2)、求α的大小.20. 已知关于x的一元二次方程 有两个实数根x1 , x2.(1)、求实数k的取值范围;(2)、是否存在实数k使得 成立?若存在,请求出k的值;若不存在,请说明理由.21. 如图,一次函数 的图象分别交x轴、y轴于C,D两点,交反比例函数 图象于A( ,4),B(3,m)两点.
(1)、求证:△AB′M≌△AD′N;(2)、求α的大小.20. 已知关于x的一元二次方程 有两个实数根x1 , x2.(1)、求实数k的取值范围;(2)、是否存在实数k使得 成立?若存在,请求出k的值;若不存在,请说明理由.21. 如图,一次函数 的图象分别交x轴、y轴于C,D两点,交反比例函数 图象于A( ,4),B(3,m)两点.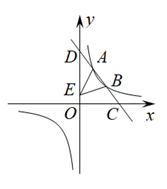 (1)、求直线CD的表达式;(2)、点E是线段OD上一点,若 ,求E点的坐标;(3)、请你根据图象直接写出不等式 的解集.22. 如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O , 点D为⊙O上一点,且CD=CB , 连接DO并延长交CB的延长线于点E , 连接OC .
(1)、求直线CD的表达式;(2)、点E是线段OD上一点,若 ,求E点的坐标;(3)、请你根据图象直接写出不等式 的解集.22. 如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O , 点D为⊙O上一点,且CD=CB , 连接DO并延长交CB的延长线于点E , 连接OC .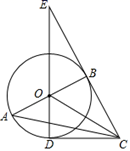 (1)、判断直线CD与⊙O的位置关系,并说明理由;(2)、若BE= ,DE=3,求⊙O的半径及AC的长.23. 寒冬来临,豆丝飘香,豆丝是鄂州民间传统美食;某企业接到一批豆丝生产任务,约定这批豆丝的出厂价为每千克4元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,新工人李明第1天生产100千克豆丝,由于不断熟练,以后每天都比前一天多生产20千克豆丝;设李明第x天( ,且x为整数)生产y千克豆丝,解答下列问题:
(1)、判断直线CD与⊙O的位置关系,并说明理由;(2)、若BE= ,DE=3,求⊙O的半径及AC的长.23. 寒冬来临,豆丝飘香,豆丝是鄂州民间传统美食;某企业接到一批豆丝生产任务,约定这批豆丝的出厂价为每千克4元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,新工人李明第1天生产100千克豆丝,由于不断熟练,以后每天都比前一天多生产20千克豆丝;设李明第x天( ,且x为整数)生产y千克豆丝,解答下列问题: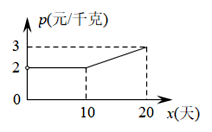 (1)、求y与x的关系式,并求出李明第几天生产豆丝280千克?(2)、设第x天生产的每千克豆丝的成本是p元,p与x之间满足如图所示的函数关系;若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价-成本)24. 如图,已知:抛物线 交x轴于A , C两点,交y轴于点B , 且OB=2CO.
(1)、求y与x的关系式,并求出李明第几天生产豆丝280千克?(2)、设第x天生产的每千克豆丝的成本是p元,p与x之间满足如图所示的函数关系;若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价-成本)24. 如图,已知:抛物线 交x轴于A , C两点,交y轴于点B , 且OB=2CO.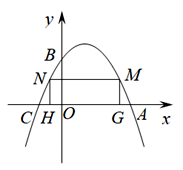
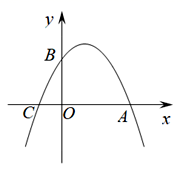 (1)、求二次函数解析式;(2)、在二次函数图象位于x轴上方部分有两个动点M、N , 且点N在点M的左侧,过M、N作x轴的垂线交x轴于点G、H两点,当四边形MNHG为矩形时,求该矩形周长的最大值;(3)、抛物线对称轴上是否存在点P , 使得△ABP为直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(1)、求二次函数解析式;(2)、在二次函数图象位于x轴上方部分有两个动点M、N , 且点N在点M的左侧,过M、N作x轴的垂线交x轴于点G、H两点,当四边形MNHG为矩形时,求该矩形周长的最大值;(3)、抛物线对称轴上是否存在点P , 使得△ABP为直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.