内蒙古通辽市科尔沁右翼中旗县2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2021-08-19 类型：期末考试

进入出卷网下载

一、单选题

1. 函数y=-x²-3的图象顶点是（）

A、 $(0 ， 3)$ B、 $(- \frac{3}{2} ， \frac{9}{4})$ C、 $(0 ， - 3)$ D、 $(- 1 ， - 3)$

查看试题解析
2. 二次函数y=x²+4x+3的图象可以由二次函数y=x²的图象平移而得到，下列平移正确的是（　　）

A、先向左平移2个单位，再先向上平移1个单位 B、先向左平移2个单位，再先向下平移1个单位 C、先向右平移2个单位，再先向上平移1个单位 D、先向右平移2个单位，再先向下平移1个单位

查看试题解析
3. 已知二次函数y＝ax²+bx+c的图象如图所示，有以下结论：①a+b+c＜0；②a﹣b+c＞1；③abc＞0；④4a﹣2b+c＜0；⑤c﹣a＞1，其中所有正确结论的序号是（）

A、①② B、①③④ C、①②③⑤ D、①②③④⑤

查看试题解析
4. 如图所示，抛物线y=ax²-x+c（a＞0）的对称轴是直线x=1，且图像经过点 P（3，0），则a+c的值为（）

A、0 B、－1 C、1 D、2

查看试题解析
5. 反比例函数y＝ $\frac{k - 1}{x}$ 的图象，在每个象限内，y的值随x值的增大而增大，则k可以为（）

A、0 B、1 C、2 D、3

查看试题解析
6. 如图，两个反比例函数 $y_{1} = \frac{4}{x}$ 和 $y = \frac{1}{x}$ 在第一象限内的图象依次是C₁和C₂ ，设点P在C₁上， $P C ⊥ x$ 轴于点C，交C₂于点A， $P D ⊥ y$ 轴于点D，交C₂于点B，则四边形PAOB的面积为（）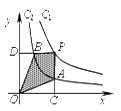

A、2 B、3 C、4 D、5

查看试题解析
7. 若 $△ A B C ∽ △ D E F$ ，相似比为2，且 $△ A B C$ 的面积为12，则 $△ D E F$ 的面积为（）

A、3 B、6 C、24 D、48

查看试题解析
8. 如图所示，给出下列条件：① $∠ B = ∠ ACD$ ；② $∠ ADC = ∠ ACB$ ；③ $\frac{A C}{C D} = \frac{A B}{B C}$ ；④ ${AC}^{2} = AD \cdot AB$ ，其中单独能够判定 $△ ABC ∽ △ ACD$ 的个数为（）

A、 $4$ B、 $3$ C、 $2$ D、 $1$

查看试题解析
9. 根据下表中的二次函数 $y = a x^{2} + b x + c$ 的自变量x与函数y的对应值，可判断该二次函数的图象与x轴（）．

$x$

…

$- 1$

$0$

$1$

$2$

…

$y$

…

$- 1$

$- \frac{7}{4}$

$- 2$

$- \frac{7}{4}$

…

A、只有一个交点 B、有两个交点，且它们分别在y轴两侧 C、有两个交点，且它们均在y轴同侧 D、无交点

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则一次函数 $y = b x + b^{2} - 4 a c$ 与反比例函数 $y = \frac{a + b + c}{x}$ 在同一坐标系内的图象大致为（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 如图，P是∠α的边OA上一点，且点P的坐标为（3，4），则sinα= ．

查看试题解析
12. 若△ABC∽△A′B′C′，且 $\frac{A B}{A' B'}$ = $\frac{3}{4}$ ，△ABC的周长为12 cm，则△A′B′C′的周长为cm.

查看试题解析
13. 将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上，点A、B的度数分别为 $86 °$ 、 $30 °$ ，则 $∠ A C B$ 的大小为

查看试题解析
14. 长为4m的梯子搭在墙上与地面成45°角，作业时调整为60°角（如图所示），则梯子的顶端沿墙面升高了 m

查看试题解析
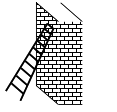15. 如图，在△ABC中，AB＝AC＝1，点D、E在直线BC上运动，设BD＝x ， CE＝y.如果∠BAC＝30°，∠DAE＝105°，则y与x之间的函数关系式为.

查看试题解析

三、解答题

16. 求值： $\frac{1}{2} \sin 60 ° \times \frac{\sqrt{2}}{2} \cos 45 °$ +2sin30°－tan60°- tan 45°

查看试题解析
17. 已知正比例函数y=k₁x(k₁≠0)与反比例函数 $y = \frac{k_{2}}{x} (k_{2} \neq 0)$ 的图象交于A、B两点，点A的坐标为（2，1）．

(1)、求正比例函数、反比例函数的表达式；

(2)、求点B的坐标．

查看试题解析
18. 如图，在某建筑物AC上，挂着一宣传条幅BC，站在点F处，测得条幅顶端B的仰角为30^° ，往条幅方向前行20米到达点E处，测得条幅顶端B的仰角为60^° ，求宣传条幅BC的长.（ $\sqrt{3} \approx 1.732$ ，结果精确到0.1米）

查看试题解析
19. 如图，一次函数y＝kx+b的图象与反比例函数y＝ $\frac{m}{x}$ 的图象交于A（﹣2，1），B（1，n）两点．

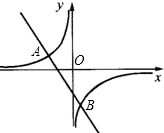(1)、求反比例函数和一次函数的解析式；

(2)、根据图象写出使一次函数的值＞反比例函数的值的x的取值范围．

查看试题解析
20. 如图，点E是四边形ABCD的对角线BD上一点，且∠BAC＝∠BDC＝∠DAE.

①试说明BE·AD＝CD·AE；

查看试题解析
21. 初三年级的一场篮球比赛中，如图队员甲正在投篮，已知球出手时离地面高 $\frac{20}{9}$ m，与篮圈中心的水平距离为7m，当球出手后水平距离为4m时到达最大高度4m，设篮球运行的轨迹为抛物线，篮圈距地面3m．

(1)、建立如图所示的平面直角坐标系，求抛物线的解析式并判断此球能否准确投中？

(2)、此时，若对方队员乙在甲前面1m处跳起盖帽拦截，已知乙的最大摸高为3.1m，那么他能否获得成功？

查看试题解析

$x$	…	$- 1$	$0$	$1$	$2$	…
$y$	…	$- 1$	$- \frac{7}{4}$	$- 2$	$- \frac{7}{4}$	…