内蒙古呼伦贝尔市海拉尔区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 剪纸是中国特有的民间艺术.在如图所示的四个剪纸图案中.既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 将抛物线 向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( ).A、 ; B、 ; C、 ; D、 .3. 已知点 在抛物线 上,则下列结论正确的是( )A、 B、 C、 D、4. 如图,PA、PB是⊙O切线,A、B为切点,点C在⊙O上,且∠ACB=55°,则∠APB等于( )
2. 将抛物线 向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( ).A、 ; B、 ; C、 ; D、 .3. 已知点 在抛物线 上,则下列结论正确的是( )A、 B、 C、 D、4. 如图,PA、PB是⊙O切线,A、B为切点,点C在⊙O上,且∠ACB=55°,则∠APB等于( )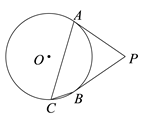 A、55° B、70° C、110° D、125°5. 下列说法正确的是( )
A、55° B、70° C、110° D、125°5. 下列说法正确的是( )①经过三个点一定可以作圆;②若等腰三角形的两边长分别为3和7,则第三边长是3或7;③一个正六边形的内角和是其外角和的2倍;④随意翻到一本书的某页,页码是偶数是随机事件;⑤关于x的一元二次方程x2-(k+3)x+k=0有两个不相等的实数根.
A、①②③ B、①④⑤ C、②③④ D、③④⑤6. 扬帆中学有一块长 ,宽 的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为 ,则可列方程为( )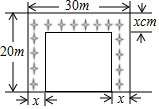 A、 B、 C、 D、7. 如图,在平面直角坐标系中,点O为坐标原点,平行四边形OABC的顶点A在反比例函数 上,顶点B在反比例函数 上,点C在x轴的正半轴上,则平行四边形OABC的面积是( )
A、 B、 C、 D、7. 如图,在平面直角坐标系中,点O为坐标原点,平行四边形OABC的顶点A在反比例函数 上,顶点B在反比例函数 上,点C在x轴的正半轴上,则平行四边形OABC的面积是( ) A、 B、 C、4 D、68. 正六边形的周长为6,则它的面积为( )A、 B、 C、 D、9. 定义新运算: ,例如: , ,则y=2⊕x(x≠0)的图象是( )A、
A、 B、 C、4 D、68. 正六边形的周长为6,则它的面积为( )A、 B、 C、 D、9. 定义新运算: ,例如: , ,则y=2⊕x(x≠0)的图象是( )A、 B、
B、 C、
C、 D、
D、 10. 如图所示,矩形纸片ABCD中,AD=6cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为( )
10. 如图所示,矩形纸片ABCD中,AD=6cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为( )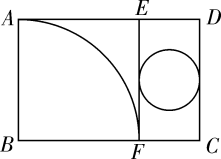 A、3.5cm B、4cm C、4.5cm D、5cm11. 如图,在 中,点 , 分别在 , 边上, , ,若 , ,则线段 的长为( )
A、3.5cm B、4cm C、4.5cm D、5cm11. 如图,在 中,点 , 分别在 , 边上, , ,若 , ,则线段 的长为( )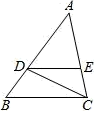 A、 B、 C、 D、512. 如图, 中, , , , 分别为边 的中点,将 绕点 顺时针旋转 到 的位置,则整个旋转过程中线段 所扫过部分的面积(即阴影部分面积)为( )
A、 B、 C、 D、512. 如图, 中, , , , 分别为边 的中点,将 绕点 顺时针旋转 到 的位置,则整个旋转过程中线段 所扫过部分的面积(即阴影部分面积)为( )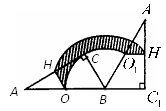 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 从一个不透明的口袋中随机摸出一球,再放回袋中,不断重复上述过程,一共摸了150次,其中有50次摸到黑球,已知口袋中仅有黑球5个和白球若干个,这些球除颜色外,其他都一样,由此估计口袋中有个白球.14. 某市为了扎实落实脱贫攻坚中“两不愁、三保障”的住房保障工作,去年已投入5亿元资金,并计划投入资金逐年增长,明年将投入7.2亿元资金用于保障性住房建设,则这两年投入资金的年平均增长率为.15. 某医药研究所开发一种新药,成年人按规定的剂量服用,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的函数关系近似满足如图所示曲线,当每毫升血液中的含药量不少于0.5毫克时治疗有效,则服药一次治疗疾病有效的时间为小时.
 16. 已知⊙O的直径AB=20,弦CD⊥AB于点E,且CD=16,则AE的长为.17. 观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2019个图形中共有个〇.
16. 已知⊙O的直径AB=20,弦CD⊥AB于点E,且CD=16,则AE的长为.17. 观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2019个图形中共有个〇.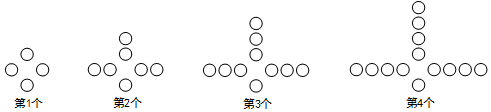
三、解答题
-
18. 计算:19. 解方程:3x(x﹣1)=2﹣2x.20. 已知:在 中, .
 (1)、求作: 的外接圆.(要求:尺规作图,保留作图痕迹,不写作法)(2)、若 的外接圆的圆心 到 边的距离为4, ,则 .21. 有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,(1)、随机从A组抽取一张,求抽到数字为2的概率;(2)、随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
(1)、求作: 的外接圆.(要求:尺规作图,保留作图痕迹,不写作法)(2)、若 的外接圆的圆心 到 边的距离为4, ,则 .21. 有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,(1)、随机从A组抽取一张,求抽到数字为2的概率;(2)、随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
22. 如图,一次函数 与反比例函数 的图象交于 、 两点,与坐标轴分别交于 、 两点. (1)、求一次函数的解析式;(2)、根据图象直接写出 中 的取值范围;(3)、求 的面积.23. 问题探究:(1)、如图①所示是一个半径为 ,高为4的圆柱体和它的侧面展开图,AB是圆柱的一条母线,一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线AB剪开,它的侧面展开图如图①中的矩形 则蚂蚁爬行的最短路程即为线段 的长)
(1)、求一次函数的解析式;(2)、根据图象直接写出 中 的取值范围;(3)、求 的面积.23. 问题探究:(1)、如图①所示是一个半径为 ,高为4的圆柱体和它的侧面展开图,AB是圆柱的一条母线,一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线AB剪开,它的侧面展开图如图①中的矩形 则蚂蚁爬行的最短路程即为线段 的长) (2)、如图②所示是一个底面半径为 ,母线长为4的圆锥和它的侧面展开图,PA是它的一条母线,一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点,求蚂蚁爬行的最短路程.(3)、如图③所示,在②的条件下,一只蚂蚁从A点出发沿圆锥的侧面爬行一周到达母线PA上的一点,求蚂蚁爬行的最短路程.24. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连接AC,过 上一点E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG.
(2)、如图②所示是一个底面半径为 ,母线长为4的圆锥和它的侧面展开图,PA是它的一条母线,一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点,求蚂蚁爬行的最短路程.(3)、如图③所示,在②的条件下,一只蚂蚁从A点出发沿圆锥的侧面爬行一周到达母线PA上的一点,求蚂蚁爬行的最短路程.24. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连接AC,过 上一点E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG. (1)、求证:EG是⊙O的切线;(2)、延长AB交GE的延长线于点M,若AH=2, ,求OM的长.25. 某商场销售一种商品的进价为每件30元,销售过程中发现月销售量y(件)与销售单价x(元)之间的关系如图所示.
(1)、求证:EG是⊙O的切线;(2)、延长AB交GE的延长线于点M,若AH=2, ,求OM的长.25. 某商场销售一种商品的进价为每件30元,销售过程中发现月销售量y(件)与销售单价x(元)之间的关系如图所示. (1)、根据图象直接写出y与x之间的函数关系式.(2)、设这种商品月利润为W(元),求W与x之间的函数关系式.(3)、这种商品的销售单价定为多少元时,月利润最大?最大月利润是多少?26. 如图,抛物线y= x2+bx+c与直线y= x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).
(1)、根据图象直接写出y与x之间的函数关系式.(2)、设这种商品月利润为W(元),求W与x之间的函数关系式.(3)、这种商品的销售单价定为多少元时,月利润最大?最大月利润是多少?26. 如图,抛物线y= x2+bx+c与直线y= x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).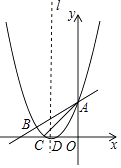 (1)、求抛物线的解析式;(2)、在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值;(3)、点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值;(3)、点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.