初中数学北师大版七年级上册第二次月考试卷A卷
试卷更新日期:2021-08-19 类型:月考试卷
一、单选题
-
1. 下列方程是一元一次方程的有( )
① ;② ;③ ;④ ;⑤ ;⑥ .
A、1个 B、2个 C、3个 D、4个2. 关于 的一元一次方程 的解为 ,则 的值为( )A、9 B、8 C、5 D、43. 下列说法中正确的是( )A、延长线段AB和延长线段BA的含义是相同的 B、延长直线AB C、射线AB和射线BA是同一条射线 D、直线AB和直线BA是同一条直线4. 小光准备从A地去往B地,打开导航、显示两地距离为37.7km,但导航提供的三条可选路线长却分别为45km,50km,51km(如图).能解释这一现象的数学知识是( )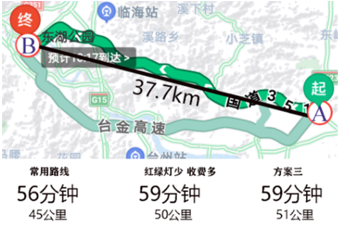 A、两点之间,线段最短 B、垂线段最短 C、三角形两边之和大于第三边 D、两点确定一条直线5. 已知线段 ,在直线AB上作线段BC , 使得 .若D是线段AC的中点,则线段AD的长为( )A、1 B、3 C、1或3 D、2或36. 点 分,时针与分针所夹的角为( )A、 B、 C、 D、7. 如图,点 在直线 上, .若 ,则 的大小为( )
A、两点之间,线段最短 B、垂线段最短 C、三角形两边之和大于第三边 D、两点确定一条直线5. 已知线段 ,在直线AB上作线段BC , 使得 .若D是线段AC的中点,则线段AD的长为( )A、1 B、3 C、1或3 D、2或36. 点 分,时针与分针所夹的角为( )A、 B、 C、 D、7. 如图,点 在直线 上, .若 ,则 的大小为( )
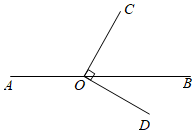 A、 B、 C、 D、8. 解一元一次方程 时,去分母正确的是( )A、 B、 C、 D、9. 从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )A、6 B、7 C、8 D、910. 某超市正在热销一种商品,其标价为每件12元,打8折销售后每件可获利2元,该商品每件的进价为( )A、7.6元 B、7.7元 C、7.8元 D、7.9元11. 已知∠AOB=70°,以O为端点作射线OC,使∠AOC=42°,则∠BOC的度数为( )A、28° B、112° C、28°或112° D、68°12. 根据图中给出的信息,下面所列方程正确的是( )
A、 B、 C、 D、8. 解一元一次方程 时,去分母正确的是( )A、 B、 C、 D、9. 从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )A、6 B、7 C、8 D、910. 某超市正在热销一种商品,其标价为每件12元,打8折销售后每件可获利2元,该商品每件的进价为( )A、7.6元 B、7.7元 C、7.8元 D、7.9元11. 已知∠AOB=70°,以O为端点作射线OC,使∠AOC=42°,则∠BOC的度数为( )A、28° B、112° C、28°或112° D、68°12. 根据图中给出的信息,下面所列方程正确的是( )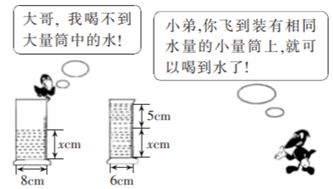 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 将两个三角尺的直角顶点重合为如图所示的位置,若 ,则 .
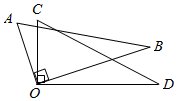 14. 如图,数轴上A、B两点所表示的数分别是-4和2, 点C是线段AB的中点,则点C所表示的数是.
14. 如图,数轴上A、B两点所表示的数分别是-4和2, 点C是线段AB的中点,则点C所表示的数是. 15. 我国古代数学著作《算学启蒙》中有这样一个数学问题,其大意是:跑得快的马每天走240里,跑得慢的马每天走150里,慢马先走12天,快马几天可以追上慢马?设快马x天可以追上慢马,根据题意,可列方程为 .16. 若 ,且 ,则关于 的一元一次方程 的解是 .17. 根据图中提供的信息,可知一把暖瓶的价格是 .
15. 我国古代数学著作《算学启蒙》中有这样一个数学问题,其大意是:跑得快的马每天走240里,跑得慢的马每天走150里,慢马先走12天,快马几天可以追上慢马?设快马x天可以追上慢马,根据题意,可列方程为 .16. 若 ,且 ,则关于 的一元一次方程 的解是 .17. 根据图中提供的信息,可知一把暖瓶的价格是 .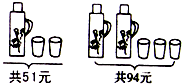 18. 已知射线 ,从 点再引射线 , ,使 , ,则 的度数为.
18. 已知射线 ,从 点再引射线 , ,使 , ,则 的度数为.三、解答题
-
19. 解方程: .20. 解方程:21. 一个学生解方程 时,去分母时,右边的1出现漏乘6,结果求出方程的解为 ,求 的值并正确的解出这个方程.22. 已知 , , 三点在同一条直线上, , , 是 的中点,求 的长.23. 已知高铁的速度比动车的速度快50 km/h,小路同学从苏州去北京游玩,本打算乘坐动车,需要6h才能到达;由于得知开通了高铁,决定乘坐高铁,她发现乘坐高铁比乘坐动车节约72 min.求高铁的速度和苏州与北京之间的距离.24. 如图
 (1)、如图,已知 , , 平分 , 平分 ,求 的度数.(2)、如果(1)中, ,其他条件不变,求 的度数.(3)、如果(1)中, , ,其他条件不变,求 的度数.25. 据国际田联《田径场地设施标准手册》,400米标准跑道由两个平行的直道和两个半径相等的弯道组成,有8条跑道,每条跑道宽1.2米,直道长87米;跑道的弯道是半圆形,环形跑道第一圈(最内圈)弯道半径为35.00米到38.00米之间.
(1)、如图,已知 , , 平分 , 平分 ,求 的度数.(2)、如果(1)中, ,其他条件不变,求 的度数.(3)、如果(1)中, , ,其他条件不变,求 的度数.25. 据国际田联《田径场地设施标准手册》,400米标准跑道由两个平行的直道和两个半径相等的弯道组成,有8条跑道,每条跑道宽1.2米,直道长87米;跑道的弯道是半圆形,环形跑道第一圈(最内圈)弯道半径为35.00米到38.00米之间.某校据国际田联标准和学校场地实际,建成第一圈弯道半径为36米的标准跑道.小王同学计算了各圈的长:
第一圈长:87×2+2π(36+1.2×0)≈400(米);
第二圈长:87×2+2π(36+1.2×1)≈408(米);
第三圈长:87×2+2π(36+1.2×2)≈415(米);
……
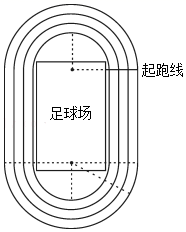
请问:
(1)、第三圈半圆形弯道长比第一圈半圆形弯道长多多少米?小王计算的第八圈长是多少?(2)、小王紧靠第一圈边线逆时针跑步、邓教练紧靠第三圈边线顺时针骑自行车(均以所靠边线长计路程),在如图的起跑线同时出发,经过20秒两人在直道第一次相遇.若邓教练平均速度是小王平均速度的2倍,求他们的平均速度各是多少?(注:在同侧直道,过两人所在点的直线与跑道边线垂直时,称两人直道相遇)
26. (问题)用n边形的对角线把n边形分割成(n-2个三角形,共有多少种不同的分割方案 ?(探究)为了解决上面的数学问题,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进转化,最后猜想得出结论.不妨假设n边形的分割方案有 种.
探究一:用四边形的对角线把四边形分割成2个三角形,共有多少种不同的分割方案?如图①,图②,显然,只有2种不同的分割方案.所以, .


探究二:用五边形的对角线把五边形分割成3个三角形,共有多少种不同的分割方案?不妨把分割方案分成三类:



第1类:如图③,用点 , 与 连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有 种不同的分割方案,所以,此类共有 种不同的分割方案.
第2类:如图④,用点 , 与 连接,把五边形分割成3个三角形,有1种不同的分割方案,可视为 种分割方案.
第3类:如图⑤,用点 , 与 连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有f(4)种不同的分割方案,所以,此类共有f(4)种不同的分割方案.
所以, (种)
探究三:用六边形的对角线把六边形分割成4个三角形,共有多少种不同的分割方案?不妨把分割方案分成四类:
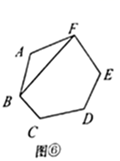
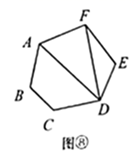
第1类:如图⑥,用 , 与 连接,先把六边形分割转化成1个三角形和1个五边形,再把五边形分割成3个三角形,由探究二知,有 种不同的分割方案,所以,此类共有 种不同的分割方案.
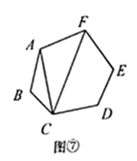
第2类:如图⑦,用 , 与 连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有 种不同的分割方案.所以,此类共有 种分割方案.
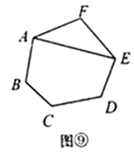
第3类:如图⑧,用 , 与 连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有 种不同的分割方案.所以,此类共有 种分割方案.
第4类:如图,用 , 与 连接,先把六边形分割转化成1个三角形和1个五边形,再把五边形分割成3个三角形,由探究二知,有 种不同的分割方案.所以,此类共有 种分割方案.
所以,
(种)
探究四:用七边形的对角线把七边形分割成5个三角形,则 与 的关系为 ,共有种不同的分割方案.
……
(结论)用 边形的对角线把 边形分割成 个三角形,共有多少种不同的分割方案 ?(直接写出 与 之间的关系式,不写解答过程)
(应用)用九边形的对角线把九边形分割成7个三角形,共有多少种不同的分割方案?(应用上述结论中的关系式求解)