安徽中考数学真题模拟题分类卷5 图形的变换
试卷更新日期:2021-08-18 类型:二轮复习
一、单选题
-
1. 一个由圆柱和圆锥组成的几何体如图水平放置,它的俯视图是( )
 A、
A、 B、
B、 C、
C、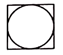 D、
D、 2. 如图所示几何体的俯视图是( )
2. 如图所示几何体的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 一个由正方体和球体组成的几何体如图水平放置,这个几何体的左视图是( )
3. 一个由正方体和球体组成的几何体如图水平放置,这个几何体的左视图是( ) A、
A、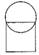 B、
B、 C、
C、 D、
D、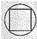 4. 几何体的三视图如图所示,这个几何体是( )
4. 几何体的三视图如图所示,这个几何体是( )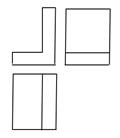 A、
A、 B、
B、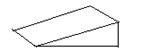 C、
C、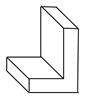 D、
D、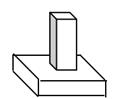 5. 下列四个几何体中,主视图为三角形的是( )A、
5. 下列四个几何体中,主视图为三角形的是( )A、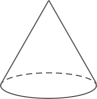 B、
B、 C、
C、 D、
D、 6. 如图,在科Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G,若EF=EG,则CD的长为( )
6. 如图,在科Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G,若EF=EG,则CD的长为( )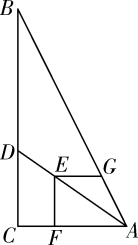 A、3.6 B、4 C、4.8 D、57. 一个由圆柱和圆锥组成的几何体如图水平放置,其主(正)视图为( )
A、3.6 B、4 C、4.8 D、57. 一个由圆柱和圆锥组成的几何体如图水平放置,其主(正)视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
8. 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( ) A、4 B、4 C、6 D、49.
A、4 B、4 C、6 D、49.如图,一个放置在水平桌面上的圆柱,它的主(正)视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,在矩形ABCD中,AD=5,AB=3 ,点E在AB上, = ,在矩形内找一点P,使得∠BPE=60°,则线段PD的最小值为( )
10. 如图,在矩形ABCD中,AD=5,AB=3 ,点E在AB上, = ,在矩形内找一点P,使得∠BPE=60°,则线段PD的最小值为( ) A、4 B、2 C、2 -2 D、2 -411. 如图,已知圆锥的三视图所示,则这个圆锥的侧面展开图扇形的圆心角的度数为( )
A、4 B、2 C、2 -2 D、2 -411. 如图,已知圆锥的三视图所示,则这个圆锥的侧面展开图扇形的圆心角的度数为( ) A、270° B、216° C、108° D、135°12. 如图,在 ABC中,AB=BC=3,∠ABC=30°,点P为 ABC内一点,连接PA、PB、PC,求PA+PB+PC的最小值( )
A、270° B、216° C、108° D、135°12. 如图,在 ABC中,AB=BC=3,∠ABC=30°,点P为 ABC内一点,连接PA、PB、PC,求PA+PB+PC的最小值( )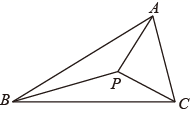 A、 B、3+ C、 D、3+13. 如图,直角 中, ,AC=8, ,点 是 内部一动点,总满足∠APC=150°,连接 ,则 的最小值为( )
A、 B、3+ C、 D、3+13. 如图,直角 中, ,AC=8, ,点 是 内部一动点,总满足∠APC=150°,连接 ,则 的最小值为( )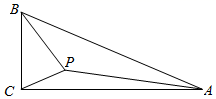 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
14. 在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片 沿过点A的直线折叠,使得点B落在 上的点 处,折痕为 ;再将 分别沿 折叠,此时点 落在 上的同一点R处.请完成下列探究:
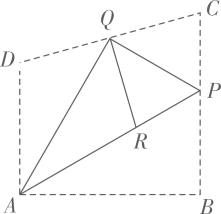 (1)、 的大小为 ;(2)、当四边形 是平行四边形时 的值为 .15. 矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数.
(1)、 的大小为 ;(2)、当四边形 是平行四边形时 的值为 .15. 矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数.
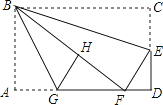
16. 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②△DEF∽△ABG;③S△ABG= S△FGH;④AG+DF=FG.
其中正确的是 . (把所有正确结论的序号都选上)
 17. 如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧 的长为 .
17. 如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧 的长为 . 18. 如图,在Rt ABC中,∠ACB=90°,AC=BC.点D、E分别在AC、BC边上,DC=EC,连接DE、AE、BD.点M、N、P分别是AE、BD、AB的中点,连接PM、PN、MN.
18. 如图,在Rt ABC中,∠ACB=90°,AC=BC.点D、E分别在AC、BC边上,DC=EC,连接DE、AE、BD.点M、N、P分别是AE、BD、AB的中点,连接PM、PN、MN.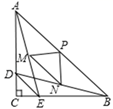 (1)、BE与MN的数量关系是;(2)、若CB=6,CE=2,在将图中的 DEC绕点C逆时针旋转一周的过程中,当B、E、D三点在一条直线上时,则MN的长度是 .19. 在数学探究活动中,“创新”小组进行了如下操作:如图,将矩形纸片ABCD的一角沿过点C的直线折叠,使得点B落在边AD的点H处,再将另一角沿过点C的直线折叠,使得点D落在CH的点Q处,两次折叠的折痕分别为CE、CF。请完成以下探究:
(1)、BE与MN的数量关系是;(2)、若CB=6,CE=2,在将图中的 DEC绕点C逆时针旋转一周的过程中,当B、E、D三点在一条直线上时,则MN的长度是 .19. 在数学探究活动中,“创新”小组进行了如下操作:如图,将矩形纸片ABCD的一角沿过点C的直线折叠,使得点B落在边AD的点H处,再将另一角沿过点C的直线折叠,使得点D落在CH的点Q处,两次折叠的折痕分别为CE、CF。请完成以下探究: (1)、∠BEC+∠DFC的大小为;(2)、若AB=3,BC=5时, 的值为。20. 如图(1),四边形 是正方形,点E是边AD上的点,将 沿着直线CE折叠,使得点D落在AC上,对应点为点F.
(1)、∠BEC+∠DFC的大小为;(2)、若AB=3,BC=5时, 的值为。20. 如图(1),四边形 是正方形,点E是边AD上的点,将 沿着直线CE折叠,使得点D落在AC上,对应点为点F. (1)、 ;(2)、如图(2),点G是BC上的点,将 沿着直线AG折叠,使得点B落在AC上,对应点为H,连接 ,则 .21. 如图,Rt△BAC , ∠ACB=30°,∠BAC=90°,将Rt△BAC绕点A旋转一定度数,点C与点C'重合,点B与点B'重合,当C、B、C'三点在同一条直线时,请完成下列探究:
(1)、 ;(2)、如图(2),点G是BC上的点,将 沿着直线AG折叠,使得点B落在AC上,对应点为H,连接 ,则 .21. 如图,Rt△BAC , ∠ACB=30°,∠BAC=90°,将Rt△BAC绕点A旋转一定度数,点C与点C'重合,点B与点B'重合,当C、B、C'三点在同一条直线时,请完成下列探究: (1)、这个旋转角=°;(2)、此时, .
(1)、这个旋转角=°;(2)、此时, .三、解答题
-
22. 学生到工厂劳动实践,学习机械零件,零件的截面如图所示,已知四边形AEFD为矩形,点B,C分别在EF,DF上,∠ABC为90°,∠BAD=53°,AB=10cm,BC=6cm,求零件的截面面积.
参考数据:sin53°≈0.80,cos53°≈0.60.
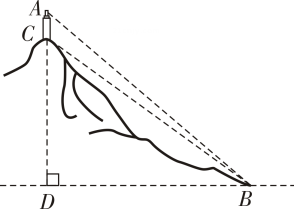
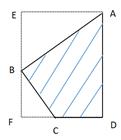 23. 如图,山顶上有一个信号塔 ,已知信号塔高 米,在山脚下点B处测得塔底C的仰角 ,塔顶A的仰角 .求山高 (点 在同一条竖直线上).
23. 如图,山顶上有一个信号塔 ,已知信号塔高 米,在山脚下点B处测得塔底C的仰角 ,塔顶A的仰角 .求山高 (点 在同一条竖直线上).(参考数据: )
 24. 筒车是我国古代发明的一种水利灌溉工具.如图1,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理.如图2,筒车盛水桶的运行轨迹是以轴心O为圆心的圆.已知圆心在水面上方,且圆被水面截得的弦AB长为6米,∠OAB=41.3°,若点C为运行轨道的最高点(C,O的连线垂直于AB),求点C到弦AB所在直线的距离.(参考数据:sin41.3°≈0.66,cos41.3°≈0.75,tan41.3°≈0.88)
24. 筒车是我国古代发明的一种水利灌溉工具.如图1,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理.如图2,筒车盛水桶的运行轨迹是以轴心O为圆心的圆.已知圆心在水面上方,且圆被水面截得的弦AB长为6米,∠OAB=41.3°,若点C为运行轨道的最高点(C,O的连线垂直于AB),求点C到弦AB所在直线的距离.(参考数据:sin41.3°≈0.66,cos41.3°≈0.75,tan41.3°≈0.88)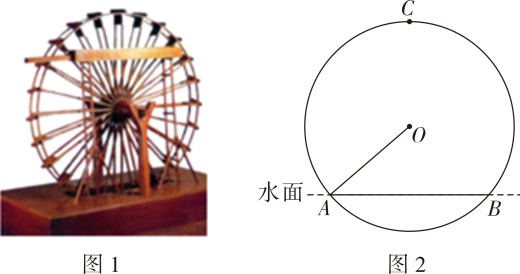 25. 为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米? (结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)
25. 为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米? (结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)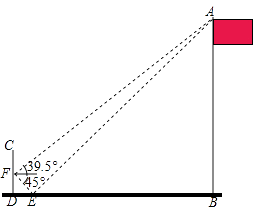 26. 如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
26. 如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.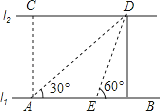 27. 中国古代人在公元前2世纪就制成了世界上最早的潜望镜,西汉初年成书的《淮南万毕术》中有这样的记载:“取大镜高悬,悬水盆于其下,则见四邻矣.”如图所示.其工作原理主要利用光的反射原理,已知 共线, 于点B,入射角 , (入射角等于反射角), 米,求OB的高度.(参考数据: )
27. 中国古代人在公元前2世纪就制成了世界上最早的潜望镜,西汉初年成书的《淮南万毕术》中有这样的记载:“取大镜高悬,悬水盆于其下,则见四邻矣.”如图所示.其工作原理主要利用光的反射原理,已知 共线, 于点B,入射角 , (入射角等于反射角), 米,求OB的高度.(参考数据: )
四、作图题
-
28. 如图,在每个小正方形的边长为1个单位的网格中,△ABC的顶点均在格点(网格线的交点)上.

⑴将△ABC向右平移5个单位得到△ ;
⑵将(1)中的△ 绕点 逆时针旋转90°得到△ ,画出△ .
29. 如图1,在由边长为 个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为端点的线段 ,线段 在网格线上,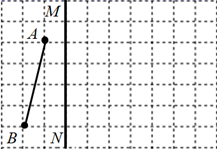 (1)、画出线段 关于线段 所在直线对称的线段 (点 分别为 的对应点);(2)、将线段 ,绕点 ,顺时针旋转 得到线段 ,画出线段 .30. 如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了格点 ABC(顶点是网格线的交点).
(1)、画出线段 关于线段 所在直线对称的线段 (点 分别为 的对应点);(2)、将线段 ,绕点 ,顺时针旋转 得到线段 ,画出线段 .30. 如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了格点 ABC(顶点是网格线的交点).
⑴请画出 ABC绕点B顺时针旋转90°得到的 A1B1C1;
⑵若平移后的 ABC与 成轴对称,请画出一种平移后的图形 A2B2C2 , 并写出平移方法.
五、综合题
-
31. 如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB=∠BPC=135°
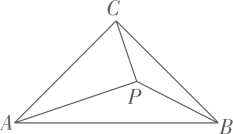 (1)、求证:△PAB∽△PBC(2)、求证:PA=2PC(3)、若点P到三角形的边AB,BC,CA的距离分别为h1 , h2 , h3 , 求证h12=h2·h332. 如图1,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E,点M为BD中点,CM的延长线交AB于点F.
(1)、求证:△PAB∽△PBC(2)、求证:PA=2PC(3)、若点P到三角形的边AB,BC,CA的距离分别为h1 , h2 , h3 , 求证h12=h2·h332. 如图1,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E,点M为BD中点,CM的延长线交AB于点F. (1)、求证:CM=EM;(2)、若∠BAC=50°,求∠EMF的大小;(3)、如图2,若△DAE≌△CEM,点N为CM的中点,求证:AN∥EM.
(1)、求证:CM=EM;(2)、若∠BAC=50°,求∠EMF的大小;(3)、如图2,若△DAE≌△CEM,点N为CM的中点,求证:AN∥EM. 33.
33.如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.
 (1)、试在图中标出点D,并画出该四边形的另两条边;(2)、将四边形ABCD向下平移5个单位,画出平移后得到的四边形A′B′C′D′.34. 图1是我国某型号隐形战斗机模型,全动型后掠翼垂尾是这款战斗机亮点之一,图2是垂尾模型的轴切面,并通过垂尾模型的外围测得如下数据,BC=8,DC=2,∠D=135°,∠C=60°,且AB//CD,求出垂尾在机身附着处的轴线AB的长.
(1)、试在图中标出点D,并画出该四边形的另两条边;(2)、将四边形ABCD向下平移5个单位,画出平移后得到的四边形A′B′C′D′.34. 图1是我国某型号隐形战斗机模型,全动型后掠翼垂尾是这款战斗机亮点之一,图2是垂尾模型的轴切面,并通过垂尾模型的外围测得如下数据,BC=8,DC=2,∠D=135°,∠C=60°,且AB//CD,求出垂尾在机身附着处的轴线AB的长. 35. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点)及过格点的直线l.
35. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点)及过格点的直线l. (1)、画出△ABC关于直线l对称的△A1B1C1;(2)、将△ABC向上平移3个单位长度,再向左平移1个单位长度,画出平移后的△A2B2C2;(3)、以A、A1、A2为顶点的三角形中,tan∠A2AA1= .36. 如图, 且 于点 ,DC⊥BC于点C , , .
(1)、画出△ABC关于直线l对称的△A1B1C1;(2)、将△ABC向上平移3个单位长度,再向左平移1个单位长度,画出平移后的△A2B2C2;(3)、以A、A1、A2为顶点的三角形中,tan∠A2AA1= .36. 如图, 且 于点 ,DC⊥BC于点C , , . (1)、求 , 的值;(2)、连接 ,求 的长.37. 如图1,在四边形ABCD中,∠ABC=∠BCD,点E在边BC上,且AE∥CD,DE∥AB,CF∥AD交线段AE于点F,连接BF.
(1)、求 , 的值;(2)、连接 ,求 的长.37. 如图1,在四边形ABCD中,∠ABC=∠BCD,点E在边BC上,且AE∥CD,DE∥AB,CF∥AD交线段AE于点F,连接BF. (1)、求证:△ABF≌△EAD;(2)、如图2,若AB=9,CD=5,∠ECF=∠AED,求BE的长;(3)、如图3,若BF的延长线经过AD的中点M,求 的值.38. 如图1,A,B分别在射线OA,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点.
(1)、求证:△ABF≌△EAD;(2)、如图2,若AB=9,CD=5,∠ECF=∠AED,求BE的长;(3)、如图3,若BF的延长线经过AD的中点M,求 的值.38. 如图1,A,B分别在射线OA,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点. (1)、求证:△PCE≌△EDQ;(2)、延长PC,QD交于点R.
(1)、求证:△PCE≌△EDQ;(2)、延长PC,QD交于点R.①如图1,若∠MON=150°,求证:△ABR为等边三角形;
②如图3,若△ARB∽△PEQ,求∠MON大小和 的值.
39. 在Rt△ABC中,∠BAC=90°,过点C的直线l∥AB,点G是BC边上一点,连接AG,过点C作GE⊥AG交l于点E,连接AE。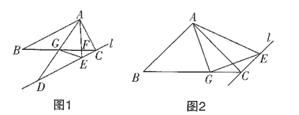 (1)、如图1,当G为BC的中点时,设AE交BC于点F,延长AG交l于点D。
(1)、如图1,当G为BC的中点时,设AE交BC于点F,延长AG交l于点D。①求证:AE=DE;
②求证:
(2)、如图2,当∠B=45°时,求 的值。40. 如图,点 的坐标为 ,点 的坐标为①以点 为旋转中心,将 顺时针方向旋转90°,得到 ;
②以点 为位似中心,将 放大 ,使相似比为 ,且点 在第三象限.
(1)、在图中画出 和 ;(2)、请直接写出点 的坐标:( , )(3)、在上面的(2)问下,直接写出在线段 上的任意动点 的对应点 的坐标:( , ).