安徽中考数学真题模拟题分类卷4 图形的性质
试卷更新日期:2021-08-18 类型:二轮复习
一、单选题
-
1. 两个直角三角板如图摆放,其中∠BAC=∠EDF=90°,∠E=45°,∠C=30°,AB与DF交于点M,若BC∥EF,则∠BMD的大小为( )
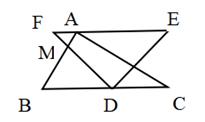 A、60° B、67.5° C、75° D、82.5°2. 已知点 在 上.则下列命题为真命题的是( )A、若半径 平分弦 .则四边形 是平行四边形 B、若四边形 是平行四边形.则 C、若 .则弦 平分半径 D、若弦 平分半径 .则半径 平分弦3. 如图, 中, ,点D在 上, .若 ,则 的长度为( )
A、60° B、67.5° C、75° D、82.5°2. 已知点 在 上.则下列命题为真命题的是( )A、若半径 平分弦 .则四边形 是平行四边形 B、若四边形 是平行四边形.则 C、若 .则弦 平分半径 D、若弦 平分半径 .则半径 平分弦3. 如图, 中, ,点D在 上, .若 ,则 的长度为( )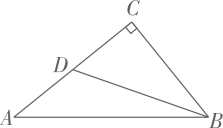 A、 B、 C、 D、44. ▱ABCD中,E,F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A、 B、 C、 D、44. ▱ABCD中,E,F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A、BE=DF B、AE=CF C、AF//CE D、∠BAE=∠DCF5. 如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( ) A、 B、2 C、 D、6. 如图,AB是⊙O的直径,BD,CD为⊙O的两条弦,且BD=CD。若∠AOC=80°,则∠B的度数为( )
A、 B、2 C、 D、6. 如图,AB是⊙O的直径,BD,CD为⊙O的两条弦,且BD=CD。若∠AOC=80°,则∠B的度数为( ) A、20° B、25° C、30° D、35°7. 四边形 中, ,点P,Q是对角线BD上不同的两点,若四边形 是菱形,则下列说法中错误的是 ( )A、 B、 C、 D、8. 如图.在 中, ,D是边AB的中点,E是边BC上一点.若DE平分 的周长,则DE的长为( )
A、20° B、25° C、30° D、35°7. 四边形 中, ,点P,Q是对角线BD上不同的两点,若四边形 是菱形,则下列说法中错误的是 ( )A、 B、 C、 D、8. 如图.在 中, ,D是边AB的中点,E是边BC上一点.若DE平分 的周长,则DE的长为( )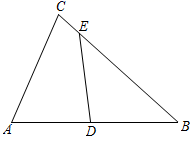 A、 B、 C、 D、19. 如图,一副直角三角板的顶点 重合( , ),当 时,则∠ABD=( )
A、 B、 C、 D、19. 如图,一副直角三角板的顶点 重合( , ),当 时,则∠ABD=( ) A、105° B、75° C、85° D、95°10. 如图,点 , , , 都在⊙O上,且 ,AB=AD , S四边形ABCD =( )
A、105° B、75° C、85° D、95°10. 如图,点 , , , 都在⊙O上,且 ,AB=AD , S四边形ABCD =( ) A、 B、 C、 D、611. 在△ABC中∠ACB=90°,分别过点B,C作∠BAC平分线的垂线,垂足分别为点D,E,BC的中点是M,连接CD,MD,ME.则下列结论错误的是( )A、CD=2ME B、ME∥AB C、BD=CD D、ME=MD12. 如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H.则四边形EFGH的周长为( )
A、 B、 C、 D、611. 在△ABC中∠ACB=90°,分别过点B,C作∠BAC平分线的垂线,垂足分别为点D,E,BC的中点是M,连接CD,MD,ME.则下列结论错误的是( )A、CD=2ME B、ME∥AB C、BD=CD D、ME=MD12. 如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H.则四边形EFGH的周长为( )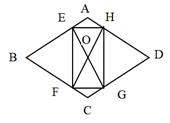 A、 B、 C、 D、13. 如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P在正方形的边上,则满足PE+PF=9的点P的个数是( )
A、 B、 C、 D、13. 如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P在正方形的边上,则满足PE+PF=9的点P的个数是( )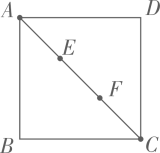 A、0 B、4 C、6 D、8
A、0 B、4 C、6 D、8二、填空题
-
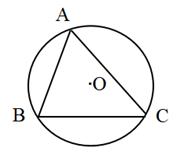
14. 命题“如果a+b=0,那么a,b互为相反数”的逆命题为.15. 如图,圆O的半径为1,△ABC内接于圆O,若∠A=60°,∠B=75°,则AB=.
 16. 如图,△ABC内接于☉O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D,若☉O的半径为2,则CD的长为
16. 如图,△ABC内接于☉O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D,若☉O的半径为2,则CD的长为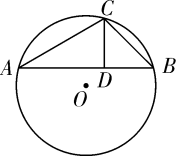 17. 如图,菱形ABOC的AB,AC分别与⊙O相切于点D、E,若点D是AB的中点,则∠DOE.
17. 如图,菱形ABOC的AB,AC分别与⊙O相切于点D、E,若点D是AB的中点,则∠DOE.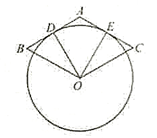 18. 如图, , ,∠BEC=40°,则 °.
18. 如图, , ,∠BEC=40°,则 °.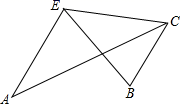
三、解答题
-
19. 如图,圆O中两条互相垂直的弦AB,CD交于点E.
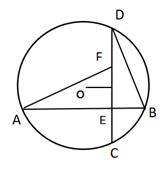 (1)、M是CD的中点,OM等于3,CD=12,求圆O的半径长;(2)、点F在CD上,且CE=EF,求证:AF⊥BD.20. 如图, 是半圆O的直径, 是半圆O上不同于 的两点 与 相交于点 是半圆O所任圆的切线,与 的延长线相交于点E,
(1)、M是CD的中点,OM等于3,CD=12,求圆O的半径长;(2)、点F在CD上,且CE=EF,求证:AF⊥BD.20. 如图, 是半圆O的直径, 是半圆O上不同于 的两点 与 相交于点 是半圆O所任圆的切线,与 的延长线相交于点E,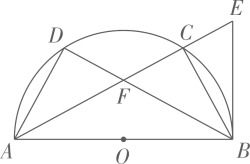 (1)、求证: ;(2)、若 求 平分 .21. 如图1.已知四边形 是矩形.点E在 的延长线上. 与 相交于点G,与 相交于点(1)、求证: ;(2)、若 ,求 的长;
(1)、求证: ;(2)、若 求 平分 .21. 如图1.已知四边形 是矩形.点E在 的延长线上. 与 相交于点G,与 相交于点(1)、求证: ;(2)、若 ,求 的长;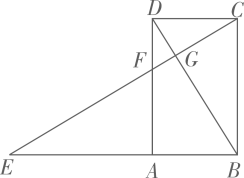 (3)、如图2,连接 ,求证: .
(3)、如图2,连接 ,求证: .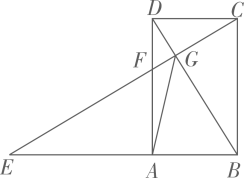 22. 如图,在边长为1个单位长度的小正方形组成的12×12的网格中,给出了以格点(网格线的交点)为端点的线段A
22. 如图,在边长为1个单位长度的小正方形组成的12×12的网格中,给出了以格点(网格线的交点)为端点的线段AB.
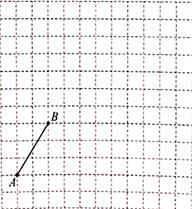 (1)、将线段AB向右平移5个单位,再向上平移3个单位得到线段CD,请画出线段C
(1)、将线段AB向右平移5个单位,再向上平移3个单位得到线段CD,请画出线段CD.
(2)、以线段CD为一边,作一个菱形CDEF,且点E,F也为格点.(作出一个菱形即可)23. 如图,点E在▱ABCD内部,AF∥BE,DF∥CE.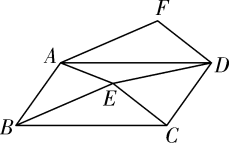 (1)、求证:△BCE≌△ADF;(2)、设▱ABCD的面积为S,四边形AEDF的面积为T,求 的值24. 如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知点O,A,B均为网格线的交点.
(1)、求证:△BCE≌△ADF;(2)、设▱ABCD的面积为S,四边形AEDF的面积为T,求 的值24. 如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知点O,A,B均为网格线的交点. (1)、①在给定的网格中,以点O为位似中心,将线段AB放大为原来的2倍,得到线段 (点A,B的对应点分别为 ).画出线段 ;
(1)、①在给定的网格中,以点O为位似中心,将线段AB放大为原来的2倍,得到线段 (点A,B的对应点分别为 ).画出线段 ;②将线段 绕点 逆时针旋转90°得到线段 .画出线段 ;
(2)、以 为顶点的四边形 的面积是个平方单位.25. 如图,以 为底的等腰 的三个顶点都在 上,过点 A作 交 的反向延长线于点D . (1)、求证: 是 的切线;(2)、若四边形 是平行四边形,且 ,求 的半径.26. 如图,四边形ABCD为菱形,BD为对角线,以AB为直径的⊙O交AD于点E,交BD于点F,⊙O的切线BG交CD于点G。
(1)、求证: 是 的切线;(2)、若四边形 是平行四边形,且 ,求 的半径.26. 如图,四边形ABCD为菱形,BD为对角线,以AB为直径的⊙O交AD于点E,交BD于点F,⊙O的切线BG交CD于点G。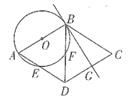 (1)、求证:DE=DC;(2)、若⊙O的直径为5,DF= ,求DE的长。27. 如图,在 中,以O为圆心,OA为半径的圆与BC相切与点B,与OC相交于点D.
(1)、求证:DE=DC;(2)、若⊙O的直径为5,DF= ,求DE的长。27. 如图,在 中,以O为圆心,OA为半径的圆与BC相切与点B,与OC相交于点D. (1)、求 的度数.(2)、如图,点E在⊙O上,连接CE与⊙O交于点F,若 ,求 的度数.28. 笔记本电脑为外出工作提供了极大的便利,其配件电脑支架也是我们用笔记本电脑办公时不可或缺的。如图1为某笔记本电脑支架的侧面(边沿部分忽略不计),我们抽象出如图2的几何图形,测得∠A照30°,AB=AC=20cm,D为AB上一点,且∠BCD=30°,求BC的长。
(1)、求 的度数.(2)、如图,点E在⊙O上,连接CE与⊙O交于点F,若 ,求 的度数.28. 笔记本电脑为外出工作提供了极大的便利,其配件电脑支架也是我们用笔记本电脑办公时不可或缺的。如图1为某笔记本电脑支架的侧面(边沿部分忽略不计),我们抽象出如图2的几何图形,测得∠A照30°,AB=AC=20cm,D为AB上一点,且∠BCD=30°,求BC的长。

