初中数学北师大版七年级上册期中考试A卷
试卷更新日期:2021-08-18 类型:期中考试
一、单选题
-
1. 2020年12月30日盐城至南通高速铁路开通运营,盐通高铁总投资约2628000万元,将数据2628000用科学记数法表示为( )A、 B、 C、 D、2. 如图所示,将平面图形绕轴旋转一周,得到的几何体是( )
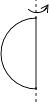 A、
A、 B、
B、 C、
C、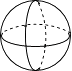 D、
D、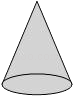 3. 将正方体的表面沿某些棱剪开,展成如图所示的平面图形,则原正方体中与数字5所在的面相对的面上标的数字为( )
3. 将正方体的表面沿某些棱剪开,展成如图所示的平面图形,则原正方体中与数字5所在的面相对的面上标的数字为( ) A、1 B、2 C、3 D、44. 已知x2﹣3x﹣12=0,则代数式﹣3x2+9x+5的值是( )A、31 B、﹣31 C、41 D、﹣415. 实数 、 在数轴上的对应点的位置如图所示,下列式子成立的是( )
A、1 B、2 C、3 D、44. 已知x2﹣3x﹣12=0,则代数式﹣3x2+9x+5的值是( )A、31 B、﹣31 C、41 D、﹣415. 实数 、 在数轴上的对应点的位置如图所示,下列式子成立的是( ) A、 B、 C、 D、6. 点A在数轴上,点A所对应的数用 表示,且点A到原点的距离等于3,则a的值为( )A、 或1 B、 或2 C、 D、17. 计算22+(-1)0的结果是( ).
A、 B、 C、 D、6. 点A在数轴上,点A所对应的数用 表示,且点A到原点的距离等于3,则a的值为( )A、 或1 B、 或2 C、 D、17. 计算22+(-1)0的结果是( ).
A、5 B、4 C、3 D、28. 下列运算正确的是( )A、3x+2x=5x2 B、3x-2x=x C、3x·2.x=6.x D、3.x÷2x=9. 如果3ab2m-1与9abm+1是同类项,那么m等于( )A、2 B、1 C、﹣1 D、010. 下列去括号正确的是( )A、 B、 C、 D、11. 如图1,将边长为的大正方形减去一个边长为1的小正方形(阴影部分),并将剩余部分延虚线剪开,得到两个长方形,再将两个长方形拼成图2所示长方形.这两个图能解释下列哪个等式( )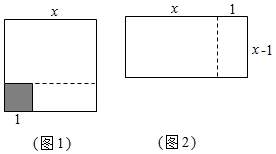 A、 B、 C、 D、12. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
A、 B、 C、 D、12. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( ) A、84 B、336 C、510 D、1326
A、84 B、336 C、510 D、1326二、填空题
-
13. 某地某天早晨的气温是 ℃,到中午升高了 ℃,晚上又降低了 ℃.那么晚上的温度是 .14. 若单项式am﹣2bn+7与单项式﹣3a4b4的和仍是一个单项式,则m﹣n=.15. 各顶点都在方格纸的格点(横竖格子线的交错点)上的多边形称为格点多边形,它的面积S可用公式 (a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克(Pick)定理”.如图给出了一个格点五边形,则该五边形的面积 .
 16. 某数学老师在课外活动中做了一个有趣的游戏:首先发给A,B,C三个同学相同数量的扑克牌(假定发到每个同学手中的扑克牌数量足够多),然后依次完成下列三个步骤:
16. 某数学老师在课外活动中做了一个有趣的游戏:首先发给A,B,C三个同学相同数量的扑克牌(假定发到每个同学手中的扑克牌数量足够多),然后依次完成下列三个步骤:第一步,A同学拿出二张扑克牌给B同学;
第二步,C同学拿出三张扑克牌给B同学;
第三步,A同学手中此时有多少张扑克牌,B同学就拿出多少张扑克牌给A同学,
请你确定,最终B同学手中剩余的扑克牌的张数为 .
17. 如图,将正整数按此规律排列成数表,则2021是表中第行第列. 18. 已知a,b,c都是有理数,且满足 =1,那么6﹣ =.
18. 已知a,b,c都是有理数,且满足 =1,那么6﹣ =.三、解答题
-
19. 计算(1)、(2)、20. 计算(1)、 ;(2)、21. 如图,请你求出阴影部分的面积(用含有x的代数式表示).
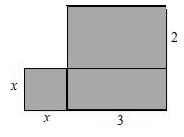 22. 先化简,再求值: ,其中 , .23. 先化简,再求值: ,其中 , .24. 将8个同样大小的小正方体搭成如图所示的几何体,请按照要求解答下列问题:(1)、从正面、左面、上面观察如图所示的几何体,分别画出所看到的几何体的形状图;
22. 先化简,再求值: ,其中 , .23. 先化简,再求值: ,其中 , .24. 将8个同样大小的小正方体搭成如图所示的几何体,请按照要求解答下列问题:(1)、从正面、左面、上面观察如图所示的几何体,分别画出所看到的几何体的形状图;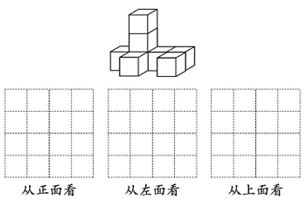 (2)、如果在这个几何体上再摆放一个相同的小正方体,并保持这个几何体从上面看和从左面看到的形状图不变.
(2)、如果在这个几何体上再摆放一个相同的小正方体,并保持这个几何体从上面看和从左面看到的形状图不变.①添加小正方体的方法共有_▲__种;
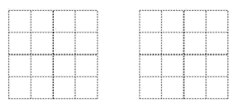
②请画出两种添加小正方体后,从正面看到的几何体的形状图.
 25. 我县某电器商场正在销售一种微波炉和电磁炉,微波炉每台定价700元,电磁炉每台定价200元.该商场决定在“双十二”期间开展促销活动,于是向客户提供两种优惠方案.
25. 我县某电器商场正在销售一种微波炉和电磁炉,微波炉每台定价700元,电磁炉每台定价200元.该商场决定在“双十二”期间开展促销活动,于是向客户提供两种优惠方案.方案一:买一台微波炉送一台电磁炉;
方案二:微波炉和电磁炉都按定价的 付款.
现一工厂老总要到该商场购买微波炉10台,电磁炉a台 .
(1)、试求出该老总按两种方案购买各自所需的费用. 用含a的代数式表示(2)、若 ,请比较此时应按哪种方案购买较为合算?(3)、当 时,你能给出一种更为省钱的购买方案吗?试写出你的设想,并求出此时的购买费用.26. 2019年国庆节,全国从1日到7日放假七天,高速公路免费通行,各地景区游人如织.其中,某著名景点,在9月30日的游客人数为0.9万人,接下来的七天中,每天的游客人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数).日期
10月1日
10月2日
10月3日
10月4日
10月5日
10月6日
10月7日
人数变化(万人)
+3.1
+1.78
-0.58
-0.8
-1
-1.6
-1.15
(1)、10月3日的人数为万人.(2)、七天假期里,游客人数最多的是10月日,达到万人;游客人数最少的是10月日,达到万人.(3)、请问此风景区在这八天内一共接待了多少游客?(4)、如果你也打算在下一个国庆节出游此景点,对出行的日期有何建议?