新疆历年中考数学真题分类卷5 图形的变换
试卷更新日期:2021-08-18 类型:二轮复习
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图所示,该几何体的俯视图是( )
2. 如图所示,该几何体的俯视图是( ) A、
A、 B、
B、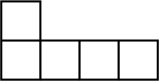 C、
C、 D、
D、 3. 如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
3. 如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )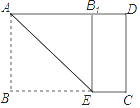 A、6cm B、4cm C、3cm D、2cm4. 如图是由三个相同的小正方体组成的几何体,则该几何体的左视图是( )
A、6cm B、4cm C、3cm D、2cm4. 如图是由三个相同的小正方体组成的几何体,则该几何体的左视图是( )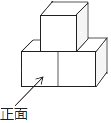 A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )
5. 如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )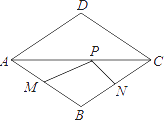 A、 B、1 C、 D、26. 如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4 且∠AFG=60°,GE=2BG,则折痕EF的长为( )
A、 B、1 C、 D、26. 如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4 且∠AFG=60°,GE=2BG,则折痕EF的长为( )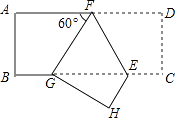 A、1 B、 C、2 D、7. 如图,是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是( )
A、1 B、 C、2 D、7. 如图,是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是( ) A、π B、2π C、4π D、5π8. 某几何体的三视图如图所示,则该几何体是( )
A、π B、2π C、4π D、5π8. 某几何体的三视图如图所示,则该几何体是( ) A、球 B、圆柱 C、三棱锥 D、圆锥9. 轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里.
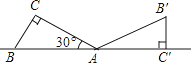
A、球 B、圆柱 C、三棱锥 D、圆锥9. 轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里.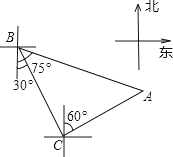 A、25 B、25 C、50 D、2510.
A、25 B、25 C、50 D、2510.如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是( )
 A、60° B、90° C、120° D、150°11. 如图,在△ABC中,D、E分别是AB、AC的中点,下列说法中不正确的是( )
A、60° B、90° C、120° D、150°11. 如图,在△ABC中,D、E分别是AB、AC的中点,下列说法中不正确的是( )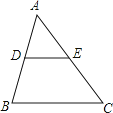 A、DE= BC B、 C、△ADE∽△ABC D、S△ADE:S△ABC=1:2
A、DE= BC B、 C、△ADE∽△ABC D、S△ADE:S△ABC=1:2二、填空题
-
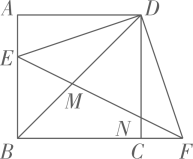
12. 如图,已知正方形ABCD边长为1,E为AB边上一点,以点D为中心,将 按逆时针方向旋转得 ,连接EF,分別交BD,CD于点M,N.若 ,则 .
 13. 如图,⊙O的半径是2,扇形BAC的圆心角为60°.若将扇形BAC剪下围成一个圆锥,则此圆锥的底面圆的半径为.
13. 如图,⊙O的半径是2,扇形BAC的圆心角为60°.若将扇形BAC剪下围成一个圆锥,则此圆锥的底面圆的半径为. 14. 如图,在△ABC中,∠A=90°,∠B=60°,AB=2,若D是BC边上的动点,则2AD+DC的最小值为.
14. 如图,在△ABC中,∠A=90°,∠B=60°,AB=2,若D是BC边上的动点,则2AD+DC的最小值为. 15. 如图,△ABC是⊙O的内接正三角形,⊙O的半径为2,则图中阴影部的面积是 .
15. 如图,△ABC是⊙O的内接正三角形,⊙O的半径为2,则图中阴影部的面积是 .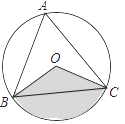 16. 如图所示,△ABC中,E,F分别是边AB,AC上的点,且满足 ,则△AEF与△ABC的面积比是 .
16. 如图所示,△ABC中,E,F分别是边AB,AC上的点,且满足 ,则△AEF与△ABC的面积比是 .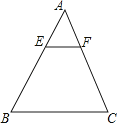
三、解答题
-
17. 如图,AC是⊙O的直径,BC,BD是⊙O的弦,M为BC的中点,OM与BD交于点F,过点D作 ,交BC的延长线于点E,且CD平分 .
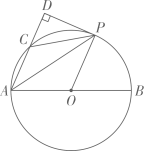
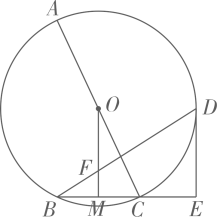 (1)、求证:DE是⊙O的切线;(2)、求证: ;(3)、若 , ,求BF的长.18. 如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.
(1)、求证:DE是⊙O的切线;(2)、求证: ;(3)、若 , ,求BF的长.18. 如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.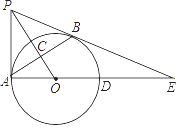 (1)、求证:PB是⊙O的切线;
(1)、求证:PB是⊙O的切线;
(2)、若OC=3,AC=4,求sinE的值.19. 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D.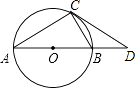 (1)、求证:△ADC∽△CDB;(2)、若AC=2,AB= CD,求⊙O半径.20. 如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF= ∠CAB.
(1)、求证:△ADC∽△CDB;(2)、若AC=2,AB= CD,求⊙O半径.20. 如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF= ∠CAB.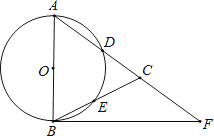 (1)、求证:直线BF是⊙O的切线;(2)、若AB=5,sin∠CBF= ,求BC和BF的长.21. 如图,楼顶上有一个广告牌AB,从与楼BC相距15 m的D处观测广告牌顶部A的仰角为 ,观测广告牌底部B的仰角为 ,求广告牌AB的高度(结果保留小数点后一位,参考数据: , , , , ).
(1)、求证:直线BF是⊙O的切线;(2)、若AB=5,sin∠CBF= ,求BC和BF的长.21. 如图,楼顶上有一个广告牌AB,从与楼BC相距15 m的D处观测广告牌顶部A的仰角为 ,观测广告牌底部B的仰角为 ,求广告牌AB的高度(结果保留小数点后一位,参考数据: , , , , ).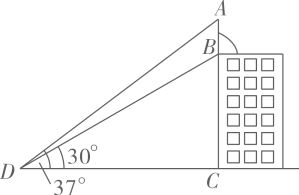 22. 如图,为测量建筑物CD的高度,在A点测得建筑物顶部D点的仰角为22°,再向建筑物CD前进30米到达B点,测得建筑物顶部D点的仰角为58°(A,B,C三点在一条直线上),求建筑物CD的高度.(结果保留整数.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
22. 如图,为测量建筑物CD的高度,在A点测得建筑物顶部D点的仰角为22°,再向建筑物CD前进30米到达B点,测得建筑物顶部D点的仰角为58°(A,B,C三点在一条直线上),求建筑物CD的高度.(结果保留整数.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)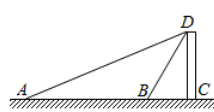 23. 如图,甲、乙为两座建筑物,它们之间的水平距离BC为30m,在A点测得D点的仰角∠EAD为45°,在B点测得D点的仰角∠CBD为60°,求这两座建筑物的高度(结果保留根号)
23. 如图,甲、乙为两座建筑物,它们之间的水平距离BC为30m,在A点测得D点的仰角∠EAD为45°,在B点测得D点的仰角∠CBD为60°,求这两座建筑物的高度(结果保留根号)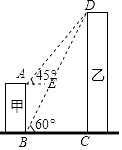 24. 如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30°,再向旗杆的方向前进16米,到达点D处(C、D、B三点在同一直线上),又测得旗杆顶端A的仰角为45°,请计算旗杆AB的高度(结果保留根号)
24. 如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30°,再向旗杆的方向前进16米,到达点D处(C、D、B三点在同一直线上),又测得旗杆顶端A的仰角为45°,请计算旗杆AB的高度(结果保留根号)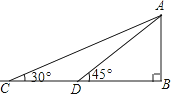 25. 如图,在数学活动课上,小丽为了测量校园内旗杆AB的高度,站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.已知旗杆与教学楼的距离BD=9m,请你帮她求出旗杆的高度(结果保留根号).
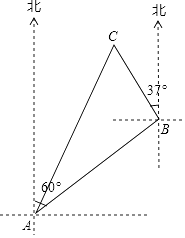
25. 如图,在数学活动课上,小丽为了测量校园内旗杆AB的高度,站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.已知旗杆与教学楼的距离BD=9m,请你帮她求出旗杆的高度(结果保留根号). 26. 一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8, ≈1.732,结果取整数)
26. 一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8, ≈1.732,结果取整数)