新疆历年中考数学真题分类卷4 图形的性质
试卷更新日期：2021-08-18 类型：二轮复习
一、单选题
-
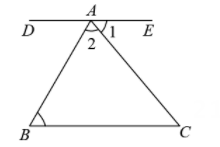
1. 如图，直线DE过点A，且 .若 ， ，则 的度数为（ ）
A、 B、 C、 D、2. 如图，AB∥CD，点E在线段BC上，CD=CE．若∠ABC=30°，则∠D为（ ）
A、85° B、75° C、60° D、30°3. 如图，⊙O的半径OD垂直于弦AB，垂足为点C，连接AO并延长交⊙O于点E，连接BE，CE．若AB=8，CD=2，则△BCE的面积为（ ）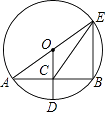
A、12 B、15 C、16 D、184. 如图，AB∥CD，∠A=50°，∠C=30°，则∠AEC等于（ ）
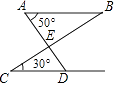A、20° B、50° C、80° D、100°5. 一个扇形的圆心角是120°，面积为3πcm2 ， 那么这个扇形的半径是（ ）A、1cm B、3cm C、6cm D、9cm6. 如图，在Rt 中， ， ， ， 于点D，E是AB的中点，则DE的长为（ ）
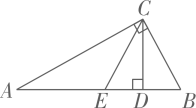A、1 B、2 C、3 D、47. 如图，在△ABC中，∠A=90°，D是AB的中点，过点D作BC的平行线交AC于点E，作BC的垂线交BC于点F，若AB=CE，且△DFE的面积为1，则BC的长为（ ）
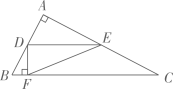A、 B、5 C、4 D、108. 如果n边形每一个内角等于与它相邻外角的2倍，则n的值是（ ）A、4 B、5 C、6 D、79. 如图，直线a∥b，∠1=72°，则∠2的度数是（ ）
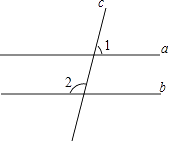A、118° B、108° C、98° D、72°10.如图，AB∥CD，CE平分∠BCD，∠B=36°，则∠DCE等于（ ）
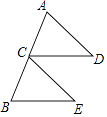
A、18° B、36° C、45° D、54°11.如图，在△ABC和△DEF中，∠B=∠DEF，AB=DE，添加下列一个条件后，仍然不能证明△ABC≌△DEF，这个条件是（ ）
A、∠A=∠D B、BC=EF C、∠ACB=∠F D、AC=DF12.如图，直线a∥b，直线c与直线a，b相交，若∠1=56°，则∠2等于（ ）
A、24° B、34° C、56° D、124°二、填空题
-
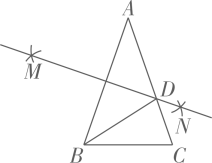
13. 四边形的外角和等于.14. 如图，在 中， ， ，分别以点A，B为圆心，大于 的长为半径作弧，两弧相交于M，N两点，作直线MN交AC于点D，连接BD，则 .
15. 如图，若AB∥CD，∠A=110°，则∠1=°.
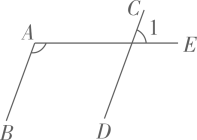16. 用等分圆周的方法，在半径为1的图中画出如图所示图形，则图中阴影部分面积为 ．
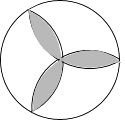17. 如图，在菱形ABCD中，∠DAB=60°，AB=2，则菱形ABCD的面积为 ．
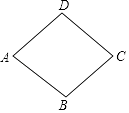18.如图，在▱ABCD中，P是CD边上一点，且AP和BP分别平分∠DAB和∠CBA，若AD=5，AP=8，则△APB的周长是 ．
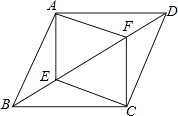
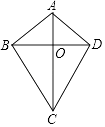
19.如图，测量河宽AB（假设河的两岸平行），在C点测得∠ACB=30°，D点测得∠ADB=60°，又CD=60m，则河宽AB为m（结果保留根号）．
20. 如图，在四边形ABCD中，AB=AD，CB=CD，对角线AC，BD相交于点O，下列结论中：①∠ABC=∠ADC；
②AC与BD相互平分；
③AC，BD分别平分四边形ABCD的两组对角；
④四边形ABCD的面积S= AC•BD．
正确的是（填写所有正确结论的序号）
三、解答题
-
21. 如图，在矩形ABCD中，点E在边BC上，点F在BC的延长线上，且 .
求证：
(1)、 ；(2)、四边形AEFD是平行四边形.22. 如图，四边形ABCD是平行四边形，DE∥BF，且分别交对角线AC于点E，F，连接BE，DF.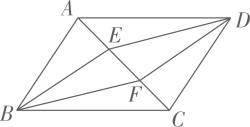
(1)、求证：AE=CF；(2)、若BE=DE，求证：四边形EBFD为菱形.23. 如图，▱ABCD的对角线AC，BD相交于点O．E，F是AC上的两点，并且AE=CF，连接DE，BF．
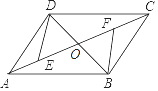(1)、求证：△DOE≌△BOF；
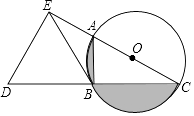
(2)、若BD=EF，连接FB，DF．判断四边形EBFD的形状，并说明理由．24.如图，在⊙O中，半径OA⊥OB，过点OA的中点C作FD∥OB交⊙O于D、F两点，且CD= ，以O为圆心，OC为半径作 ，交OB于E点．
(1)、求⊙O的半径OA的长；(2)、计算阴影部分的面积．25. 如图，四边形ABCD是平行四边形，E，F是对角线BD上的两点，且BF=ED，求证：AE∥CF．
