新疆历年中考数学真题分类卷3 函数综合
试卷更新日期:2021-08-18 类型:二轮复习
一、单选题
-
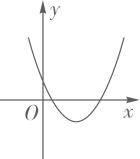
1. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象可能是( )
 A、
A、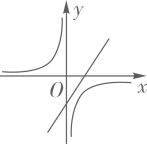 B、
B、 C、
C、 D、
D、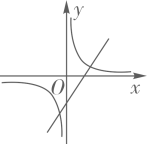 2. 一次函数y=kx+b(k,b是常数,k≠0)的图象,如图所示,则不等式kx+b>0的解集是( )
2. 一次函数y=kx+b(k,b是常数,k≠0)的图象,如图所示,则不等式kx+b>0的解集是( )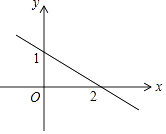 A、x<2 B、x<0 C、x>0 D、x>23.
A、x<2 B、x<0 C、x>0 D、x>23.如图,点A(a,3),B(b,1)都在双曲线y= 上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )
 A、 B、 C、 D、4. 小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列图中表示小明的父亲离家的距离与时间的函数图象是( )A、
A、 B、 C、 D、4. 小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列图中表示小明的父亲离家的距离与时间的函数图象是( )A、 B、
B、 C、
C、 D、
D、 5.
5.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
 A、a>0 B、c<0 C、3是方程ax2+bx+c=0的一个根 D、当x<1时,y随x的增大而减小6. 已知A(x1 , y1),B(x2 , y2)是反比例函数y= (k≠0)图象上的两个点,当x1<x2<0时,y1>y2 , 那么一次函数y=kx﹣k的图象不经过( )
A、a>0 B、c<0 C、3是方程ax2+bx+c=0的一个根 D、当x<1时,y随x的增大而减小6. 已知A(x1 , y1),B(x2 , y2)是反比例函数y= (k≠0)图象上的两个点,当x1<x2<0时,y1>y2 , 那么一次函数y=kx﹣k的图象不经过( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图,在矩形ABCD中, , .点P从点A出发,以2cm/s的速度在矩形的边上沿 运动,当点P与点D重合时停止运动.设运动的时间为 (单位:s), 的面积为S(单位: ),则S随t变化的函数图象大致为( )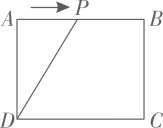 A、
A、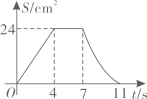 B、
B、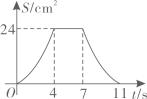 C、
C、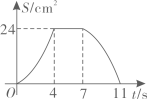 D、
D、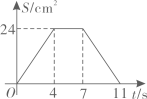
二、填空题
-
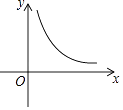
8. 点(﹣1,2)所在的象限是第象限.9. 如图,它是反比例函数y= 图象的一支,根据图象可知常数m的取值范围是 .
 10. 若点 , 在反比例函 的图象上,则 (填“>“<”或“=”).11. 如图,在x轴,y轴上分别截取OA,OB,使OA=OB,再分别以点A,B为圆心,以大于 AB长为半径画弧,两弧交于点P.若点P的坐标为(a,2a-3),则a的值为.
10. 若点 , 在反比例函 的图象上,则 (填“>“<”或“=”).11. 如图,在x轴,y轴上分别截取OA,OB,使OA=OB,再分别以点A,B为圆心,以大于 AB长为半径画弧,两弧交于点P.若点P的坐标为(a,2a-3),则a的值为. 12. 如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们规定:当x取任意一个值时,x对应的函数值分别为y1和y2 , 若y1≠y2 , 取y1和y2中较小值为M;若y1=y2 , 记M=y1=y2 . ①当x>2时,M=y2;②当x<0时,M随x的增大而增大;③使得M大于4的x的值不存在;④若M=2,则x=1.上述结论正确的是(填写所有正确结论的序号).
12. 如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们规定:当x取任意一个值时,x对应的函数值分别为y1和y2 , 若y1≠y2 , 取y1和y2中较小值为M;若y1=y2 , 记M=y1=y2 . ①当x>2时,M=y2;②当x<0时,M随x的增大而增大;③使得M大于4的x的值不存在;④若M=2,则x=1.上述结论正确的是(填写所有正确结论的序号).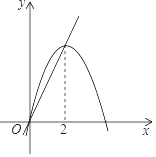 13. 如图,抛物线y=ax2+bx+c过点(﹣1,0),且对称轴为直线x=1,有下列结论:
13. 如图,抛物线y=ax2+bx+c过点(﹣1,0),且对称轴为直线x=1,有下列结论:①abc<0;②10a+3b+c>0;③抛物线经过点(4,y1)与点(﹣3,y2),则y1>y2;④无论a,b,c取何值,抛物线都经过同一个点(﹣ ,0);⑤am2+bm+a≥0,其中所有正确的结论是 .
 14. 如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为 s时,四边形EFGH的面积最小,其最小值是 cm2 .
14. 如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为 s时,四边形EFGH的面积最小,其最小值是 cm2 .
三、综合题
-
15. 如图,一次函数 与反比例函数 的图象交于点 , .
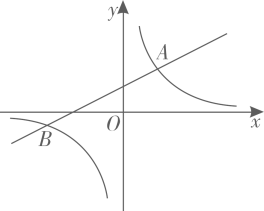 (1)、求反比例函数和一次函数的解析式;(2)、判断点 是否在一次函数 的图象上,并说明理由;(3)、直接写出不等式 的解集.16. 已知反比例函数y= 的图象与一次函数y=kx+m的图象交于点(2,1).
(1)、求反比例函数和一次函数的解析式;(2)、判断点 是否在一次函数 的图象上,并说明理由;(3)、直接写出不等式 的解集.16. 已知反比例函数y= 的图象与一次函数y=kx+m的图象交于点(2,1).
(1)、分别求出这两个函数的解析式;
(2)、判断P(﹣1,﹣5)是否在一次函数y=kx+m的图象上,并说明原因.17. 如图,在平面直角坐标系中,抛物线y= x2﹣ x﹣4与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.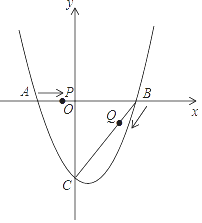 (1)、求点A,B,C的坐标;
(1)、求点A,B,C的坐标;
(2)、点P从A点出发,在线段AB上以每秒2个单位长度的速度向B点运动,同时,点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,当其中一个点到达终点时,另一个点也停止运动.设运动时间为t秒,求运动时间t为多少秒时,△PBQ的面积S最大,并求出其最大面积;(3)、在(2)的条件下,当△PBQ面积最大时,在BC下方的抛物线上是否存在点M,使△BMC的面积是△PBQ面积的1.6倍?若存在,求点M的坐标;若不存在,请说明理由.18. 一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示: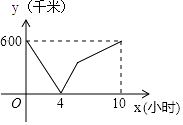 (1)、甲乙两地相距多远?(2)、求快车和慢车的速度分别是多少?(3)、求出两车相遇后y与x之间的函数关系式;(4)、何时两车相距300千米.19.
(1)、甲乙两地相距多远?(2)、求快车和慢车的速度分别是多少?(3)、求出两车相遇后y与x之间的函数关系式;(4)、何时两车相距300千米.19.如图,抛物线y=﹣ x2+ x+2与x轴交于点A,B,与y轴交于点C.
 (1)、试求A,B,C的坐标;(2)、将△ABC绕AB中点M旋转180°,得到△BAD.
(1)、试求A,B,C的坐标;(2)、将△ABC绕AB中点M旋转180°,得到△BAD.①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)、在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请直接写出所有满足条件的P点的坐标;若不存在,请说明理由.20. 某周日上午8:00小宇从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家x(小时)后,到达离家y(千米)的地方,图中折线OABCD表示y与x之间的函数关系.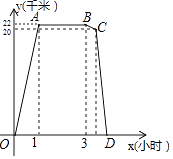 (1)、活动中心与小宇家相距千米,小宇在活动中心活动时间为小时,他从活动中心返家时,步行用了小时;(2)、求线段BC所表示的y(千米)与x(小时)之间的函数关系式(不必写出x所表示的范围);(3)、根据上述情况(不考虑其他因素),请判断小宇是否能在12:00前回到家,并说明理由.21.
(1)、活动中心与小宇家相距千米,小宇在活动中心活动时间为小时,他从活动中心返家时,步行用了小时;(2)、求线段BC所表示的y(千米)与x(小时)之间的函数关系式(不必写出x所表示的范围);(3)、根据上述情况(不考虑其他因素),请判断小宇是否能在12:00前回到家,并说明理由.21.如图,直线y=2x+3与y轴交于A点,与反比例函数y= (x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
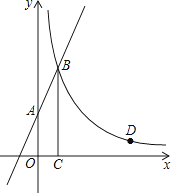 (1)、求反比例函数的解析式;(2)、点D(a,1)是反比例函数y= (x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.22.
(1)、求反比例函数的解析式;(2)、点D(a,1)是反比例函数y= (x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.22.暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
 (1)、从小刚家到该景区乘车一共用了多少时间?(2)、求线段AB对应的函数解析式;(3)、小刚一家出发2.5小时时离目的地多远?23. 已知抛物线 .(1)、求抛物线的对称轴;(2)、把抛物线沿y轴向下平移 个单位,若抛物线的顶点落在x轴上,求a的值;(3)、设点 , 在抛物线上,若 ,求a的取值范围.24. 如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+c的顶点是A(1,3),将OA绕点O顺时针旋转90°后得到OB,点B恰好在抛物线上,OB与抛物线的对称轴交于点C.
(1)、从小刚家到该景区乘车一共用了多少时间?(2)、求线段AB对应的函数解析式;(3)、小刚一家出发2.5小时时离目的地多远?23. 已知抛物线 .(1)、求抛物线的对称轴;(2)、把抛物线沿y轴向下平移 个单位,若抛物线的顶点落在x轴上,求a的值;(3)、设点 , 在抛物线上,若 ,求a的取值范围.24. 如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+c的顶点是A(1,3),将OA绕点O顺时针旋转90°后得到OB,点B恰好在抛物线上,OB与抛物线的对称轴交于点C.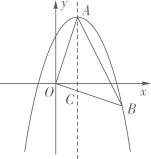 (1)、求抛物线的解析式;(2)、P是线段AC上一动点,且不与点A,C重合,过点P作平行于x轴的直线,与△OAB的边分别交于M,N两点,将△AMN以直线MN为对称轴翻折,得到△A′MN,设点P的纵坐标为m.
(1)、求抛物线的解析式;(2)、P是线段AC上一动点,且不与点A,C重合,过点P作平行于x轴的直线,与△OAB的边分别交于M,N两点,将△AMN以直线MN为对称轴翻折,得到△A′MN,设点P的纵坐标为m.①当△A′MN在△OAB内部时,求m的取值范围;
②是否存在点P,使S△A′MN= S△OA′B , 若存在,求出满足条件m的值;若不存在,请说明理由.
25.如图,抛物线y=ax2+bx+c(a≠0)与直线y=x+1相交于A(﹣1,0),B(4,m)两点,且抛物线经过点C(5,0).
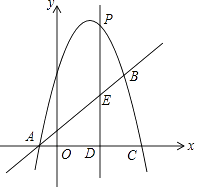 (1)、求抛物线的解析式;(2)、点P是抛物线上的一个动点(不与点A、点B重合),过点P作直线PD⊥x轴于点D,交直线AB于点E.
(1)、求抛物线的解析式;(2)、点P是抛物线上的一个动点(不与点A、点B重合),过点P作直线PD⊥x轴于点D,交直线AB于点E.①当PE=2ED时,求P点坐标;
②是否存在点P使△BEC为等腰三角形?若存在请直接写出点P的坐标;若不存在,请说明理由.
26.如图,对称轴为直线x= 的抛物线经过点A(6,0)和B(0,﹣4).
 (1)、求抛物线解析式及顶点坐标;(2)、设点E(x,y)是抛物线上一动点,且位于第一象限,四边形OEAF是以OA为对角线的平行四边形,求平行四边形OEAF的面积S与x之间的函数关系式;(3)、当(2)中的平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形.27.
(1)、求抛物线解析式及顶点坐标;(2)、设点E(x,y)是抛物线上一动点,且位于第一象限,四边形OEAF是以OA为对角线的平行四边形,求平行四边形OEAF的面积S与x之间的函数关系式;(3)、当(2)中的平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形.27.如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣ x+1与y轴交于点D.
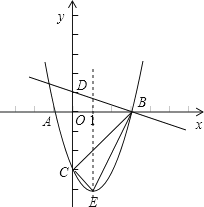 (1)、求抛物线的解析式;(2)、证明:△DBO∽△EBC;(3)、在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、证明:△DBO∽△EBC;(3)、在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.