浙江省绍兴市嵊州市2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-08-17 类型:期末考试
一、单选题
-
1. 要使二次根式 有意义,x的值可以是( )A、0 B、1 C、2 D、32. 下面四个手机应用图标中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列各式中计算正确的是( )A、3+2 =5 B、 =3 C、(2 )2=12 D、 =±34. 如图,在▱ABCD中,∠A=100°,若∠ABD:∠DBC=3:2,则∠DBC的度数为( )
3. 下列各式中计算正确的是( )A、3+2 =5 B、 =3 C、(2 )2=12 D、 =±34. 如图,在▱ABCD中,∠A=100°,若∠ABD:∠DBC=3:2,则∠DBC的度数为( ) A、32° B、40° C、48° D、60°5. 如图所示,在一边靠墙(墙足够长)的空地上,修建一个面积为375平方米的矩形临时仓库,仓库一边靠墙,另外三边用总长为55米的栅栏围成,若设栅栏AB的长为x米,则下列各方程中,符合题意的是( )
A、32° B、40° C、48° D、60°5. 如图所示,在一边靠墙(墙足够长)的空地上,修建一个面积为375平方米的矩形临时仓库,仓库一边靠墙,另外三边用总长为55米的栅栏围成,若设栅栏AB的长为x米,则下列各方程中,符合题意的是( )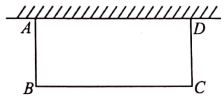 A、 x(55﹣x)=375 B、 x(55﹣2x)=375 C、x(55﹣2x)=375 D、x(55﹣x)=3756. 篮球队5名场上队员的身高(单位:cm)分别是:188,190,192,194,195.现用一名身高为191cm的队员换下身高为195cm的队员,与换人前相比,场上队员的身高( )A、平均数变小,方差变小 B、平均数变小,方差变大 C、平均数变大,方差变小 D、平均数变大,方差变大7. 一元二次方程x2-8x=48可表示成(x-a)2=48+b的形式,其中a,b为整数,求a+b之值为何( )A、20 B、12 C、-12 D、-208. 已知△ABC中,AB=AC,求证:∠B<90°,下面写出运用反证法证明这个命题的四个步骤:
A、 x(55﹣x)=375 B、 x(55﹣2x)=375 C、x(55﹣2x)=375 D、x(55﹣x)=3756. 篮球队5名场上队员的身高(单位:cm)分别是:188,190,192,194,195.现用一名身高为191cm的队员换下身高为195cm的队员,与换人前相比,场上队员的身高( )A、平均数变小,方差变小 B、平均数变小,方差变大 C、平均数变大,方差变小 D、平均数变大,方差变大7. 一元二次方程x2-8x=48可表示成(x-a)2=48+b的形式,其中a,b为整数,求a+b之值为何( )A、20 B、12 C、-12 D、-208. 已知△ABC中,AB=AC,求证:∠B<90°,下面写出运用反证法证明这个命题的四个步骤:①所以∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾 ②因此假设不成立.所以∠B<90°③假设在△ABC中,∠B≥90° ④由AB=AC,得∠C=∠B≥90°,即∠B+∠C≥180°. 这四个步骤正确的顺序应是( )
A、④③①② B、③④②① C、①②③④ D、③④①②9. 如图,在▱ABCD中,∠ADC=60°,点F在CD的延长线上,连结BF,G为BF的中点,连结AG.若AB=2,BC=6,DF=3,则AG的长为( ) A、3 B、 C、 D、10. 如图,在平面直角坐标系xOy中,菱形ABCD与菱形GFED关于点D成中心对称,点C,G在x轴的正半轴上,点A,F在反比例函数y= (k>0,x>0)的图象上,延长AB交x轴于点P(1,0),若∠APO=120°,则k的值是( )
A、3 B、 C、 D、10. 如图,在平面直角坐标系xOy中,菱形ABCD与菱形GFED关于点D成中心对称,点C,G在x轴的正半轴上,点A,F在反比例函数y= (k>0,x>0)的图象上,延长AB交x轴于点P(1,0),若∠APO=120°,则k的值是( )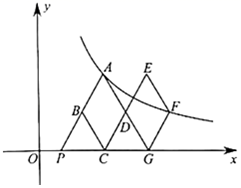 A、3 B、3 C、6 D、6
A、3 B、3 C、6 D、6二、填空题
-
11. 化简: =.12. 已知一个多边形的每一个外角都等于72°,则这个多边形的边数是.13. 在一次体检中,某班学生视力检查结果如表:
视力
4.7以下
4.7
4.8
4.9
5.0
5.0以上
所占比例
5%
8%
5%
40%
30%
12%
从表中看出全班视力的众数是 .
14. 关于x的一元二次方程x2﹣3x+m=0有两个不相等的实数根,写出一个满足条件的实数m的值 .(写出一个即可)15. 如图,在菱形ABCD中,对角线AC,BD相交于点O,若AC=6,BD=8,则菱形ABCD的周长是.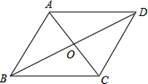 16. 已知近视眼镜的度数D(度)与镜片焦距f(米)成反比例关系,且400度近视眼镜镜片的焦距为0.25米.小慧原来戴400度的近视眼镜,经过一段时间的矫正治疗后,现在只需戴镜片焦距为0.4米的眼镜了,则小慧所戴眼镜的度数降低了 度.17. 若关于x的一元二次方程ax2+bx+6=0的一个根为x=﹣2,则代数式6a﹣3b+2的值为 .18. 对于反比例函数y=﹣ ,当y<5且y≠0时,x的取值范围为 .19. 如图,四边形ABCD和AEFG均为正方形,点G在对角线BD上,点F在边BC上,连结BE.若DG=3 ,BF=1,则正方形ABCD的边长为 .
16. 已知近视眼镜的度数D(度)与镜片焦距f(米)成反比例关系,且400度近视眼镜镜片的焦距为0.25米.小慧原来戴400度的近视眼镜,经过一段时间的矫正治疗后,现在只需戴镜片焦距为0.4米的眼镜了,则小慧所戴眼镜的度数降低了 度.17. 若关于x的一元二次方程ax2+bx+6=0的一个根为x=﹣2,则代数式6a﹣3b+2的值为 .18. 对于反比例函数y=﹣ ,当y<5且y≠0时,x的取值范围为 .19. 如图,四边形ABCD和AEFG均为正方形,点G在对角线BD上,点F在边BC上,连结BE.若DG=3 ,BF=1,则正方形ABCD的边长为 . 20. 如图1,在▱ABCD中(AB>BC),∠DAB=60°,对角线AC,BD相交于点E,动点P由点A出发,沿A→B→C运动.设点P的运动路程为x,△AEP的面积为y,y与x的函数关系图象如图2所示,当△AEP为等腰三角形时,x的值为 .
20. 如图1,在▱ABCD中(AB>BC),∠DAB=60°,对角线AC,BD相交于点E,动点P由点A出发,沿A→B→C运动.设点P的运动路程为x,△AEP的面积为y,y与x的函数关系图象如图2所示,当△AEP为等腰三角形时,x的值为 .
三、解答题
-
21. 计算:(1)、(3+ )(3﹣ );(2)、 .22. 解方程:(1)、(x+1)2=16;(2)、2x2﹣5x+3=0.23. 某校七年级举行庆祝建党100周年知识竞赛,现分别从三个班中各随机抽取10名同学的成绩(单位:分)收集数据如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
60
70
80
90
100
1班
0
1
6
2
1
2班
1
1
3
4
1
3班
1
1
4
2
2
分析数据:
平均数
中位数
众数
1班
83
80
80
2班
83
b
90
3班
a
80
80
根据以上信息回答下列问题:
(1)、请直接写出分析数据表格中a,b的值.(2)、比较这三组样本数据的平均数、中位数、众数,你认为哪个班的成绩比较好?请说明理由.(3)、学校将给竞赛成绩100分的同学颁发奖状,该校七年级学生共570人,试估计需要准备多少张奖状.24. 如图,菱形ABCD的对角线交于点O,点E是菱形外一点,DE∥AC,CE∥BD. (1)、求证:四边形DECO是矩形;(2)、连接AE交BD于点F,当∠ADB=30°,DE=3时,求菱形ABCD的面积.25. 如图,在平面直角坐标系xOy中,一次函数y=x+2的图象与x轴,y轴分别交于点A和点B,与反比例函数y= (k>0,x>0)的图象交于点C,B为线段AC的中点.
(1)、求证:四边形DECO是矩形;(2)、连接AE交BD于点F,当∠ADB=30°,DE=3时,求菱形ABCD的面积.25. 如图,在平面直角坐标系xOy中,一次函数y=x+2的图象与x轴,y轴分别交于点A和点B,与反比例函数y= (k>0,x>0)的图象交于点C,B为线段AC的中点. (1)、求点A的坐标.(2)、求k的值.(3)、点D为线段AC上的一个动点,过点D作DE∥x轴,交该反比例函数图象于点E,连结OD,OE.若△ODE的面积为 ,求点D的坐标.26. 如图,在平面直角坐标系xOy中,正方形OABC的顶点A,C分别落在x轴,y轴上,点B的坐标为(8,8),点D在线段BC上(不与B,C重合),将△OCD沿OD翻折,使得点C落在同一平面内的点E处.
(1)、求点A的坐标.(2)、求k的值.(3)、点D为线段AC上的一个动点,过点D作DE∥x轴,交该反比例函数图象于点E,连结OD,OE.若△ODE的面积为 ,求点D的坐标.26. 如图,在平面直角坐标系xOy中,正方形OABC的顶点A,C分别落在x轴,y轴上,点B的坐标为(8,8),点D在线段BC上(不与B,C重合),将△OCD沿OD翻折,使得点C落在同一平面内的点E处. (1)、如图1,当OD=10时.
(1)、如图1,当OD=10时.①求点D的坐标.
②延长DE交AB于点F,求点F的坐标.
(2)、连结BE并延长,交正方形OABC的边于点G,若BD=OG,求点D的坐标.