吉林省吉林市永吉县2021年中考数学一模试卷
试卷更新日期：2021-08-17 类型：中考模拟
一、单选题
-
1. ﹣3的绝对值是（ ）A、﹣3 B、3 C、- D、2. 下图是由4个相同的正方体组成的立体图形，它的左视图是（ ）
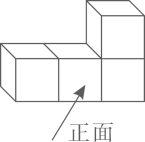A、
B、
C、
D、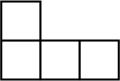
3. 下列计算正确的是（ ）A、 B、 C、 D、4. 如图，AB∥CD，AD＝CD，∠1＝70°，则∠2的度数是（ ）
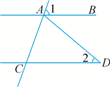A、20° B、35° C、40° D、70°5. 如图，点C在以AB为直径的⊙O上，BC＝5，∠A＝30°，则AC的长为（ ）
A、10 B、8 C、 D、6. 曲桥是我国古代经典建筑之一，它的修建增加了游人在桥上行走的路程，有利于游人更好地观赏风光。如图， 两地间修建曲桥与修建直的桥相比，增加了桥的长度，其中蕴含的数学道理是（ ）
A、两点之间，线段最短 B、平行于同一条直线的两条直线平行 C、垂线段最短 D、两点确定一条直线二、填空题
-
7. 因式分解： .
8. 公报显示，2020年我国经济运行逐步恢复常态，全年国内生产总值约为1 010 000亿元，把1 010 000这个数用科学记数法表示为 ．9. 若分式 的值为0，则x的值是 ．10. 不等式 ≥ 的解集为 ．11. 若关于x的一元二次方程 有两个不相等的实数根，则m的值可以是（写出满足正确的一个数值即可）．12. 在某一时刻，测得一根高为1.5 m的竹竿的影长为3 m，同时同地测得一栋楼的影长为60 m，则这栋楼的高度为m．13. 如图，在扇形OAB中，∠AOB＝90°．D，E分别是半径OA，OB上的点，以OD，OE为邻边的矩形ODCE的顶点C在弧AB上．若OD＝3，OE＝4，则阴影部分图形的周长是（结果保留π）．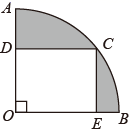
14. 如图①，在矩形纸片ABCD中，AB＝5，BC＝3，先按图②操作：将矩形ABCD沿过点A的直线折叠，使点D落在边AB上的E处，折痕为AF．再按图③操作：沿过点F的直线折叠，使点C落在边EF上的H处，折痕为FG．则阴影部分图形的面积是 ．
三、解答题
-
15. 先化简再求值： ，其中 ．16. 张翔从学校出发骑自行车去县城，中途因道路施工步行一段距离，1.5h后到达县城．他骑车的平均速度是15km/h，步行的平均速度是5km/h，路程长20km，他骑车与步行各用多少时间？17. 第一盒中有2个白球、1个黄球，第二盒中有1个白球、1个黄球．这些球除颜色外无其他差别．分别从每个盒中随机取出1个球，用画树状图（或列表）的方法，求取出的2个球中有1个白球、1个黄球的概率．18. 如图，点B，E，C，F在同一条直线上，AB＝DE，BE＝CF，AB DE．求证：△ABC≌△DEF．
19. 图1.2是两张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，线段 的两个端点均在小正方形的顶点上；
(1)、在图1中画出以 为底边的等腰直角 ，点 在小正方形顶点上；(2)、在图2中画出以 为腰的等腰 ，点 在小正方形的顶点上，且 的面积为8.20. 为了测量某单位院内旗杆AB的高度，在地面距离旗杆底部B的15米C处放置高度为1.8米的测角仪CD，测得旗杆顶端A的仰角（∠ADE）为54°．求旗杆AB的高度（结果精确到1米）．（参考数据：sin 54°≈0.81，cos 54°≈0.59，tan 54°≈1.38）
21. 为弘扬传统文化，某校开展了“传承经典文化，阅读经典名著”活动．为了解七、八年级学生（七、八年级各有600名学生）的阅读效果，该校举行了经典文化知识竞赛．现从两个年级各随机抽取20名学生的竞赛成绩（百分制）进行分析，过程如下：收集数据：
七年级：79，85，73，80，75，76，87，70，75，94，75，79，81，71，75，80，86，59，83，77
八年级：92，74，87，82，72，81，94，83，77，83，80，81，71，81，72，77，82，80，70，41
整理数据：
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
七年级
0
1
0
a
7
1
八年级
1
0
0
7
10
2
平均数
众数
中位数
七年级
78
75
b
八年级
78
c
80.5
数据应用：
(1)、由上表填空：a＝ ， b＝ ， c＝；(2)、估计该校七、八年级学生在本次竞赛中成绩在90分以上的共有多少人？(3)、你认为哪个年级的学生对经典文化知识掌握的总体水平较好，请说明理由．22. 如图，一次函数的图象与反比例函数的图象相交于点A（2，1），B（—1，n）两点．
(1)、求n的值；(2)、连接OA和OB，则△OAB的面积为 ．23. 某街道需要铺设管线的总长为9000 m，原计划由甲、乙两队共同施工，工作一段时间后，因甲队另有工作任务，余下的由乙队单独完成．已知甲队每天完成150 m，如图是表示剩余管线的长度y（m）与乙队工作时间x（天）之间的函数关系图象．
(1)、乙队每天完成 m，a＝；(2)、求线段AB所对应的函数解析式，并写出自变量x的取值范围；(3)、管线铺设完成，需要天．24. 如图，已知在△ABC中，点D，E，F分别为AB，BC，AC的中点，连接DF，EF，BF．
(1)、求证：四边形BEFD是平行四边形；(2)、若∠AFB＝90°，①求证：四边形BEFD是菱形；
② BC＝6，则四边形BEFD的周长为 ▲ _．
25. 如图，在△ABC中，∠C＝90°，AC＝BC＝4，P，Q两点同时从C出发，点P 以每秒2个单位长度的速度沿CB向终点B运动；点Q 以每秒1个单位长度的速度沿CA向终点A运动，以CP，CQ为邻边作矩形CPMQ．当点P停止运动时，点Q继续向终点A运动．设点Q的运动时间为t秒．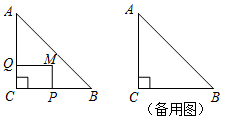
(1)、在点P的运动过程中，CQ＝ ， BP＝（用含t的代数式表示）；(2)、当点M落在AB边上时，t ＝s；(3)、设矩形CPMQ与△ABC重合部分图形的面积为S，求S与t之间的函数关系式；26.(1)、如图①，在平面直角坐标系中，抛物线 与x轴相交于A，B两点（点A在点B的左侧），与y轴相交于点C（0，3），顶点为D
①求抛物线的解析式；
②求△ABD的面积．
(2)、将图①中的抛物线y轴右侧的部分沿y轴折叠到y轴的左侧，将折叠后的这部分图象与原抛物线y轴右侧的部分（包括点C）的图象组成新的图象，记为图像M，如图②．①直接写出图像M所对应的函数解析式；
②直接写出图像M所对应的函数y随x的增大而增大时x的取值范围．