浙江省宁波市江北区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{{(- 2)}^{2}} = - 2$ C、 $\sqrt{3} \times \sqrt{2} = \sqrt{6}$ D、 $\sqrt{\frac{9}{4}} = \pm \frac{3}{2}$

查看试题解析
2. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 牛顿曾说：“反证法是数学家最精良的武器之一”.用反证法证明命题“在△ABC中，若AB≠AC，则∠B≠∠C”，首先应假设（）

A、∠B＝∠C B、AB＝AC C、∠B≥∠C D、∠B≤∠C

查看试题解析
4. 一元二次方程 $3 x^{2} + 5 x + 1 = 0$ 根的情况是（）

A、没有实数根 B、有两个不相等的实数根 C、无法判断 D、有两个相等的实数根

查看试题解析
5. 关于反比例函数y＝﹣ $\frac{2}{x}$ 的图象性质，下列说法不正确的是（）

A、图象经过点（1，﹣2） B、图象位于第二、四象限 C、当x＜0时，y随x的增大而减小 D、图象关于原点对称

查看试题解析

6. 某市射击队进行队内测试，甲、乙、丙、丁四人进行十轮射击后，每个人的十次成绩的平均分和方差如下表所示：

班级	甲	乙	丙	丁
平均分	9.9	9.8	9.9	9.0
方差	4.2	5.2	5.2	4.2

则哪位队员的成绩更好（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

7. 用配方法解方程2x²﹣4x﹣1＝0时，需要先将此方程化成形如（x+m）²＝n（n≥0）的形式，则下列配方正确的是（）

A、（x﹣2）²＝5 B、（x﹣1）²＝ $\frac{3}{2}$ C、（x﹣1）²＝2 D、（x﹣1）²＝ $\frac{11}{4}$

查看试题解析
8. 如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（）

A、当AB＝BC时，它是菱形 B、当AC⊥BD时，它是菱形 C、当∠ABC＝90°时，它是矩形 D、当AC＝BD时，它是正方形

查看试题解析
9. 如图有一张长为12，宽为8的长方形（矩形）纸片，先将其上下对折，再左右对折，最后沿着虚线剪下一个直角三角形①，若该直角三角形①的直角边长为整数，将①展开可得一个四边形，则下列哪个选项不能作为该四边形的面积（）

A、18 B、24 C、28 D、30

查看试题解析
10. 如图所示，正方形ABCD的边长为4，点E为线段BC上一动点，连结AE，将AE绕点E顺时针旋转90°至EF，连结BF，取BF的中点M，若点E从点B运动至点C，则点M经过的路径长为（）

A、2 B、 $2 \sqrt{2}$ C、 $2 \sqrt{3}$ D、4

查看试题解析

二、填空题

11. 二次根式 $\sqrt{x - 3}$ 中字母x的取值范围是．

查看试题解析
12. 请写出一个位于第一、三象限的反比例函数表达式，y =.

查看试题解析
13. 两个全等的正方形如图放置，重叠部分为正八边形，且其各边长都为 $\sqrt{2}$ ，每个内角均为135°，则正方形的边长为 .

查看试题解析
14. 已知m是方程x²﹣2x﹣3＝0的一个根，则2m²﹣4m﹣1＝.

查看试题解析
15. 已知某七个数据的平均值为a，按从大到小排序，前四个数据的平均值为b，后四个数据的平均值为c，则这七个数据的中位数为 .（结果用含a，b，c的代数式表示）

查看试题解析
16. 如图，在平面直角坐标系xOy中，直线y＝kx与双曲线y＝ $\frac{k}{x}$ 相交于A，B两点，点C是第一象限内双曲线上不与点A重合的一点，连结CA并延长交y轴于点P，连结BP，BC，点A恰为PC中点.若△PBC的面积是24，则k的值为 .

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{18} - \sqrt{8}$

(2)、 $\sqrt{{(- 3)}^{2}} + 2 \sqrt{\frac{1}{3}} \times \sqrt{3}$

查看试题解析

18. 按要求解方程：

（ 1 ）小聪同学解方程的过程如下，请指出最早出现错误的步骤序号，并写出正确的解答过程.

2x（x﹣1）＝3（x﹣1）

解：两边除以（x﹣1），得2x＝3①

系数化为1，得x＝1.5②

最早出现错误的步骤序号：　

你的解答过程：

2x（x﹣1）＝3（x﹣1）

（ 2 ）小明同学解方程的过程如下，请指出最早出现错误的步骤序号，并写出正确的解答过程.

（x﹣3）²＝9

解：两边开平方，得x﹣3＝3①

移项，合并同类项，得x＝6②

最早出现错误的步骤序号：　

你的解答过程：

（x﹣3）²＝9

（ 3 ）解方程：

x²﹣4x﹣5＝0

查看试题解析

19. 如图，在7×7的正方形网格图中，线段AB的两个端点都在格点上，分别按下列要求画格点四边形.（要求图1与图2的两个四边形不全等）

(1)、在图1中画一个以AB为边的矩形；

(2)、在图2中画一个以AB为边的平行四边形且与（1）中所画的矩形面积相等.

查看试题解析
20. 为了开展阳光体育运动，提高学生身体素质，学校开设了“引体向上”课程.为了解学生做引体向上的情况，现从八年级各班随机抽取了部分男生进行测试，绘制出不完整的统计图1和图2，请根据有关信息，解答下列问题：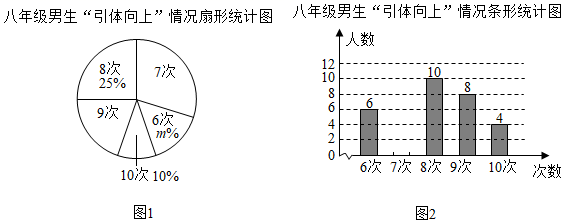

(1)、本次接受随机抽样调查的男生人数为，图1中m的值是；

(2)、本次调查获取的样本数据（6，7，8，9，10）中，众数为，中位数为；

(3)、补全条形统计图；

(4)、根据样本数据，若八年级有280名男生，请你估计该校八年级男生“引体向上”次数在8次及以上的人数.

查看试题解析
21. 如图，一次函数y＝kx+2的图象与反比例函数y＝ $\frac{m}{x}$ 的图象交于A，B两点，且A（1，3）.

(1)、分别求出一次函数和反比例函数的表达式；

(2)、求点B的坐标；

(3)、观察图象，直接写出kx+2≥ $\frac{m}{x}$ 时，x的取值范围.

查看试题解析
22. 如图，E、F、G、H分别是菱形ABCD四边上的点，且AH＝AE＝CF＝CG，连结EF、FG、GH、HE.

(1)、求证：四边形EFGH是矩形；

(2)、若∠D＝120°，S_矩形EFGH＝ $\frac{1}{3}$ S_菱形ABCD ，求 $\frac{D G}{G C}$ 的值.

查看试题解析
23. 随着宁波轨道交通4号线的开通，充满魅力的千年古城﹣﹣慈城，吸引了越来越多的游客前来.说到慈城，不得不提软糯香甜的年糕，《舌尖上的中国》专门介绍了宁波的这一特色美食.慈城某商店于今年三月初以每件40元的进价购进一批水磨年糕，当年糕售价为每件60元时，三月份共销售192件.四、五月该批年糕销售量持续走高，在售价不变的基础上，五月份的销售量达到300件.

(1)、求四、五两个月销售量的月平均增长率；

(2)、从六月份起，在五月份的基础上，商店决定采用降价促销的方式回馈顾客，经市场调查发现，该年糕每件降价1元，月销售量增加20件.在顾客获得最大实惠的前提下，当年糕每件降价多少元时，商场六月仍可获利为6080元？

查看试题解析
24. 如图1，在矩形ABCD中，点E是边AB的中点，点G是平面上一点，若在射线BC上存在一点F，使得四边形EDFG为菱形，我们称菱形EDFG是矩形ABCD的“矩菱形”.

(1)、命题“正方形的‘矩菱形’也是正方形”是；（填“真命题”或“假命题”）

(2)、如图2，矩形ABCD为正方形，四边形EDFG是其“矩菱形”，EG交BC于点H，若HE＝ $\sqrt{5}$ ，求CH的长；

(3)、假设 $\frac{A D}{A B}$ ＝k，
①若矩形ABCD始终存在“矩菱形”，求k的取值范围.

②如图3，若AB＝2，点M为菱形EDFG的中心点，连结EM、CM、CG、BG，请用含有k的代数式表示五边形EMCGB的面积S.

查看试题解析