吉林省吉林地区2021年中考数学模拟试卷
试卷更新日期:2021-08-17 类型:中考模拟
一、单选题
-
1. 如图,在数轴上,若点B表示一个负数,则原点可以是( )
 A、点E B、点D C、点C D、点A2. 如图所示的几何体是由五个小正方体搭建而成的,则从左面看得到的平面图形是( )
A、点E B、点D C、点C D、点A2. 如图所示的几何体是由五个小正方体搭建而成的,则从左面看得到的平面图形是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 2020年6月23日,北斗三号最后一颗全球组网卫星在西昌卫星发射中心成功发射并顺利进入预定轨道,它的稳定运行标志着全球四大卫星导航系统之一的中国北斗卫星导航系统全面建成.该卫星距离地面约36000千米,将数据36000用科学记数法表示为( )A、 B、 C、 D、4. 下列各图形中均有直线 ,则能使结论 成立的是( )A、
3. 2020年6月23日,北斗三号最后一颗全球组网卫星在西昌卫星发射中心成功发射并顺利进入预定轨道,它的稳定运行标志着全球四大卫星导航系统之一的中国北斗卫星导航系统全面建成.该卫星距离地面约36000千米,将数据36000用科学记数法表示为( )A、 B、 C、 D、4. 下列各图形中均有直线 ,则能使结论 成立的是( )A、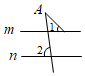 B、
B、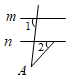 C、
C、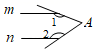 D、
D、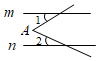 5. 永定河,“北京的母亲河”.近年来,我区政府在永定河治理过程中,有时会将弯曲的河道改直,图中A,B两地间的河道改直后大大缩短了河道的长度.这一做法的主要依据是( )
5. 永定河,“北京的母亲河”.近年来,我区政府在永定河治理过程中,有时会将弯曲的河道改直,图中A,B两地间的河道改直后大大缩短了河道的长度.这一做法的主要依据是( ) A、两点确定一条直线 B、垂线段最短 C、过一点有且只有一条直线与已知直线垂直 D、两点之间,线段最短6. 在分割矩形的课外实践活动中,甲、乙两人进行如下操作:
A、两点确定一条直线 B、垂线段最短 C、过一点有且只有一条直线与已知直线垂直 D、两点之间,线段最短6. 在分割矩形的课外实践活动中,甲、乙两人进行如下操作:甲:将矩形按图1所示分割成四个三角形,然后将四个三角形分别沿矩形的边向外翻折,得到一个面积是原来矩形面积2倍的菱形;
乙:将矩形按图2所示分割成四个三角形,然后将四个三角形分别沿矩形的边向外翻折,得到一个面积是原来矩形面积2倍的矩形.
对于这两人的操作,以下判断正确的是( )
 A、甲、乙都符合题意 B、甲、乙都不符合题意 C、甲不符合题意、乙符合题意 D、甲符合题意、乙不符合题意
A、甲、乙都符合题意 B、甲、乙都不符合题意 C、甲不符合题意、乙符合题意 D、甲符合题意、乙不符合题意二、填空题
-
7. 计算: = .8. 分解因式: = .9. 若关于 的一元二次方程 有实数根,则k的取值范围是 .10. 正六边形的一个外角的大小为度.11. 某眼镜公司积极响应国家号召,在技术顾问和市场监管局的帮助下,开始生产医用护目镜.第一周生产 个,工人在技术员的指导下,技术越来越熟练,第二周比第一周增长10%.用含 的代数式表示该公司这两周共生产医用护目镜个.
 12. 如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4m.则路灯的高度OP为m.
12. 如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4m.则路灯的高度OP为m. 13. 如图, 是 的直径,点 在 上, , , .若 的半径为1,则图中阴影部分的面积是(结果保留 ).
13. 如图, 是 的直径,点 在 上, , , .若 的半径为1,则图中阴影部分的面积是(结果保留 ). 14. 我们规定:当k,b为常数,k≠0,b≠0,k≠b时,一次函数y=kx+b与y=bx+k互为交换函数.例如:y=4x+3的交换函数为y=3x+4.一次函数y=kx+2与它的交换函数图象的交点横坐标为 .
14. 我们规定:当k,b为常数,k≠0,b≠0,k≠b时,一次函数y=kx+b与y=bx+k互为交换函数.例如:y=4x+3的交换函数为y=3x+4.一次函数y=kx+2与它的交换函数图象的交点横坐标为 .三、解答题
-
15. 以下是小华化简分式 的过程:
解:原式 ①
②
③
(1)、小华的解答过程在第步出现错误.(2)、请你帮助小华写出正确的解答过程,并计算当 时分式的值.16. 某玩具厂计划加工2700个玩具,为了尽快完成任务,实际每天加工玩具的数量是原计划的1.2倍,结果提前3天完成任务.求该玩具厂原计划每天加工这种玩具的数量.17. 如图,点E , F在BC上,AB=DC , ∠A=∠D , ∠B=∠C .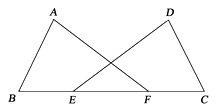
求证:BE=FC.
18. 医院准备从甲、乙、丙三位医生和A、B两名护士中选取一位医生和一名护士支援某地的防汛救灾工作.求:恰好选中医生甲和护士A的概率.19. 为提升学生阅读能力,某市某校开展“读书伴我行,书香进校园”活动,各班都设立了图书馆,学校为了解学生课外阅读的喜好,抽取部分学生进行问卷调查(每人只选一种书籍),将收集的数据整理并绘制成如图所示的两幅统计图,请根据图中的信息,完成下列问题: (1)、学校本次调查共抽取了名学生;(2)、补全条形统计图;(3)、在扇形统计图中,“漫画”所在扇形的圆心角度数为度;(4)、如果该校共有3000名学生,估计该校喜欢“文学”的学生有多少人?20. 图①、图②、图③均是 的正方形网格,每个小正方形的边长为1,每个小正方形的顶点称为格点,线段 的端点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求以 为边画 .
(1)、学校本次调查共抽取了名学生;(2)、补全条形统计图;(3)、在扇形统计图中,“漫画”所在扇形的圆心角度数为度;(4)、如果该校共有3000名学生,估计该校喜欢“文学”的学生有多少人?20. 图①、图②、图③均是 的正方形网格,每个小正方形的边长为1,每个小正方形的顶点称为格点,线段 的端点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求以 为边画 .
要求:
(1)、在图①中画一个钝角三角形,在图②中画一个直角三角形,在图③中画一个锐角三角形;(2)、三个图中所画的三角形的面积均不相等;(3)、点 在格点上.21. 宋家州主题公园拟修建一座柳宗元塑像,如图所示,柳宗元塑像(塑像中高者) 在高 的假山 上,在 处测得塑像底部 的仰角为 ,再沿 方向前进 到达 处,测得塑像顶部 的仰角为 ,求柳宗元塑像 的高度.(精确到 .参考数据: , , , )
 22. 如图,在平面直角坐标系中,反比例函数 的图象经过点A(1, 2),B(m ,n)(m>1),过点B作y轴的垂线,垂足为C.
22. 如图,在平面直角坐标系中,反比例函数 的图象经过点A(1, 2),B(m ,n)(m>1),过点B作y轴的垂线,垂足为C.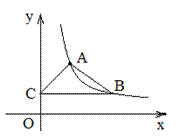 (1)、求该反比例函数解析式;(2)、当△ABC面积为2时,求点B的坐标23. 一个容积为200升的水箱,安装有A、B两个水管,加水过程中A水管始终打开,B水管可随时打开或关闭,两水管匀速为水箱加水,且水流速度为定值,当水箱加满时,加水过程结束.
(1)、求该反比例函数解析式;(2)、当△ABC面积为2时,求点B的坐标23. 一个容积为200升的水箱,安装有A、B两个水管,加水过程中A水管始终打开,B水管可随时打开或关闭,两水管匀速为水箱加水,且水流速度为定值,当水箱加满时,加水过程结束. (1)、如图是某次加水过程中水箱中水量y(升)与时间x(分)之间的函数图象.
(1)、如图是某次加水过程中水箱中水量y(升)与时间x(分)之间的函数图象.①分别求A、B两水管的水流速度.
②求y与x的函数关系式,
(2)、当水箱中无水时,13分钟将水箱加满,求A水管打开后几分钟打开B水管.24. 综合与实践在数学活动课上,老师出示了这样一个问题:如图1,在 中, , , ,点 为 边上的任意一点.将 沿过点 的直线折叠,使点 落在斜边 上的点 处.问是否存在 是直角三角形?若不存在,请说明理由;若存在,求出此时 的长度.

探究展示:勤奋小组很快找到了点 、 的位置.
如图2,作 的角平分线交 于点 ,此时 沿 所在的直线折叠,点 恰好在 上,且 ,所以 是直角三角形.
问题解决:
(1)、按勤奋小组的这种折叠方式, 的长度为 .(2)、创新小组看完勤奋小组的折叠方法后,发现还有另一种折叠方法,请在图3中画出来.(3)、在(2)的条件下,求出 的长.25. 如图,在等腰直角 中, , .动点 以每秒2个单位长度的速度沿射线 运动,过点 作 于点 ,以 , 为邻边作 ; 与等腰直角 的重叠部分面积为 (平方单位), ,点 与点 重合时运动停止,设点 的运动时间为 秒. (1)、直接写出点 落在 边上时 的值.(2)、求 与 的函数关系式.(3)、直接写出点 与 各顶点的连线平分 面积时 的值.26. 《函数的图象与性质》拓展学习展示:
(1)、直接写出点 落在 边上时 的值.(2)、求 与 的函数关系式.(3)、直接写出点 与 各顶点的连线平分 面积时 的值.26. 《函数的图象与性质》拓展学习展示: (1)、(问题)如图①,在平面直角坐标系中,抛物线 : 与 轴相交于 , 两点,与 轴交于点 ,则 , .(2)、(操作)将图①中抛物线 沿 方向平移 长度的距离得到拋物线 , 在 轴左侧的部分与 在 轴右侧的部分组成的新图象记为 ,如图②.请直接写出图象 对应的函数解析式.(3)、(探究)在图②中,过点 作直线 平行于 轴,与图象 交于 , 两点,如图③.求出图象 在直线 上方的部分对应的函数 随 的增大而增大时 的取值范围.(4)、(应用) 是抛物线 对称轴上一个动点,当 是直角三角形时,直接写出 点的坐标.
(1)、(问题)如图①,在平面直角坐标系中,抛物线 : 与 轴相交于 , 两点,与 轴交于点 ,则 , .(2)、(操作)将图①中抛物线 沿 方向平移 长度的距离得到拋物线 , 在 轴左侧的部分与 在 轴右侧的部分组成的新图象记为 ,如图②.请直接写出图象 对应的函数解析式.(3)、(探究)在图②中,过点 作直线 平行于 轴,与图象 交于 , 两点,如图③.求出图象 在直线 上方的部分对应的函数 随 的增大而增大时 的取值范围.(4)、(应用) 是抛物线 对称轴上一个动点,当 是直角三角形时,直接写出 点的坐标.