浙江省金华市金东区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-17 类型：期末考试

进入出卷网下载

一、单选题

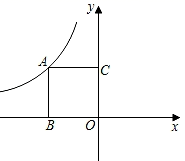
1. 式子 $\frac{1}{\sqrt{x - 1}}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x < 1$ B、 $x \leq 1$ C、 $x > 1$ D、 $x \geq 1$

查看试题解析
2. 如图，在平面直角坐标系xOy中，正方形ABOC的顶点C为（0，2），反比例函数y＝ $\frac{k}{x}$ 的图象经过点A，则k的值是（）

A、2 B、﹣2 C、4 D、﹣4

查看试题解析
3. 点A和点B关于原点成中心对称，已知点A的坐标是（3，﹣4），则点B的坐标是（）

A、（3，4） B、（﹣3，4） C、（3，﹣4） D、（4，﹣3）

查看试题解析
4. 如图，点A是直线l外一点，在l上取两点B、C，分别以A、C为圆心，BC、AB长为半径画弧，两弧交于点D，分别连接AB、AD、CD，则四边形ABCD一定是（）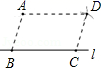

A、平行四边形 B、矩形 C、菱形 D、梯形

查看试题解析
5. 用配方法解一元二次方程 $x^{2} - 4 x = 5$ 时，此方程可变形为（）

A、 ${(x + 2)}^{2} = 1$ B、 ${(x - 2)}^{2} = 1$ C、 ${(x + 2)}^{2} = 9$ D、 ${(x - 2)}^{2} = 9$

查看试题解析
6. 将抛物线 $y = 3 x^{2}$ 向上平移3个单位，再向左平移2个单位，那么得到的抛物线的解析式为（）

A、 $y = 3 {(x + 2)}^{2} + 3$ B、 $y = 3 {(x - 2)}^{2} + 3$ C、 $y = 3 {(x + 2)}^{2} - 3$ D、 $y = 3 {(x - 2)}^{2} - 3$

查看试题解析
7. 一组数据4，3，6，9，6，5的中位数和众数分别是（）

A、5和5.5 B、5.5和6 C、5和6 D、6和6

查看试题解析
8. 某种药品原价为36元/盒，经过连续两次降价后售价为25元/盒.设平均每次降价的百分率为x，根据题意所列方程正确的是（）

A、36（1﹣x）²＝﹣25 B、36（1﹣2x）＝25 C、36（1﹣x）²＝25 D、36（1﹣x²）＝25

查看试题解析
9. 如图，在矩形ABCD中，AB=2，BC=4，对角线AC的垂直平分线分别交AD，AC于点E，O，连接CE，则CE的长为（）

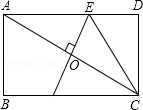A、3 B、3.5 C、2.5 D、2.8

查看试题解析
10. 已知一元二次方程 $x^{2} - 3 x - 1 = 0$ 的两个实数根分别是 x₁ 、 x₂ 则 x₁² x₂ + x₁ x₂² 的值为（）

A、-6 B、- 3 C、3 D、6

查看试题解析

二、填空题

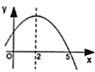
11. 当x＝2时， $\sqrt{14 + x}$ 的值是.

查看试题解析
12. 若点（4，m）与点（5，n）都在反比例函数y＝ $\frac{8}{x}$ （x≠0）的图象上，则mn（填＞，＜或＝）.

查看试题解析
13. 已知一组数据10，8，9，x，5的众数是8，那么这组数据的方差是

查看试题解析
14. 如图，是二次函数 $y = a x^{2} + b x + c$ 的部分图象，由图象可知不等式 $a x^{2} + b x + c < 0$ 的解集是.

查看试题解析
15. 已知关于 $x$ 的一元二次方程 $x^{2} + b x + b - 1 = 0$ 有两个相等的实数根，则 $b$ 的值是．

查看试题解析
16. 如图，在平面直角坐标系中，有点A（3，0），点B（3，5），射线AO上的动点C，y轴上的动点D，平面上的一个动点E，若∠CBA＝∠CBD，以点B，C，D，E为顶点的四边形是矩形，则AC的长为.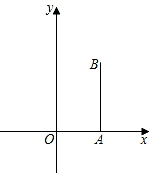

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{2}$ × $\sqrt{6}$ ；

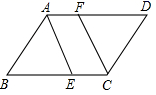
(2)、（2 $\sqrt{2}$ +3 $\sqrt{3}$ ）（3 $\sqrt{3}$ ﹣2 $\sqrt{2}$ ）.

查看试题解析
18. 解方程：

(1)、x²+5x﹣6＝0；

(2)、3x²﹣4x﹣7＝0.

查看试题解析
19. 如图，在▱ABCD中，E、F分别是BC、AD上的点，且AE∥CF，AE与CF相等吗？说明理由.

查看试题解析
20. 如图，在方格纸中，线段AB的两个端点都在小方格的格点上，分别按下列要求画格点四边形.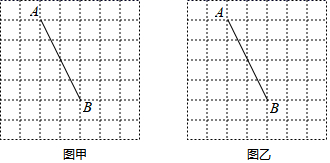

(1)、在图甲中画一个以AB为对角线的平行四边形.

(2)、在图乙中画一个以AB为边的矩形.

查看试题解析
21. 某班为充实图书角图书，在学习委员的倡议下进行了一次给班级捐书活动，受污染区域（阴影部分）记录了在相应捐书数目为N时的人数分布情况.

捐书数N

1

2

3

4

5

6

捐书N本的人数

1

2

17

■

■

4

已知捐书4本或4本以上的人平均每人捐书4.7本，捐书5本以及5本以下的同学平均捐书3.5本.问捐书4本和5本的各有多少人？

查看试题解析
22. 如图，在边长为120cm的正方形铁皮ABCD上，剪去图中阴影部分的四个全等的等腰直角三角形，再沿图中的虚线折起，折成一个长方体工艺盒（A，B，C，D四个顶点正好重合于上底面一点）.已知点M，N在CD边上，且是被剪去的一个等腰直角三角形斜边的两个端点，设CM＝DN＝x（cm）.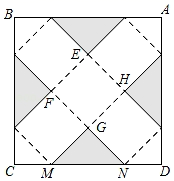

(1)、若折成的包装盒恰好是个正方体，求这个工艺盒的体积；

(2)、当x取何值时，工艺盒的四个侧面面积和S最大，最大值为多少？

查看试题解析
23. 在平面直角坐标系中，四边形ABCD是平行四边形，且A（﹣1，0），B（0，﹣ $\sqrt{3}$ ），C（3，0）.

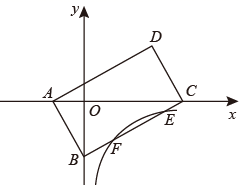(1)、求证：四边形ABCD是矩形；

(2)、若反比例函数y＝ $\frac{k}{x}$ 的图象与线段BC交于点E，F，且BF＝EF.
①求点F的横坐标；

②求k值.

查看试题解析
24. 已知在平面直角坐标系中，原点O是正方形ABCD的对角线交点，点A（0，2），过x轴正半轴上的动点P（m，0）作x轴垂线交过点B，C，D三点的抛物线于点Q.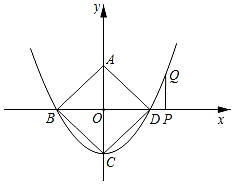

(1)、求抛物线的解析式；

(2)、是否存在四边形ACPQ为菱形，若存在，求出m值；若不在，说明理由.

(3)、连结BQ，当△BPQ有两边之比为 $\sqrt{2}$ ：1时，求m的值.

查看试题解析

捐书数N	1	2	3	4	5	6
捐书N本的人数	1	2	17	■	■	4