广东省深圳市2021年中考数学四模试卷
试卷更新日期:2021-08-17 类型:中考模拟
一、单选题
-
1. 2的相反数的倒数是( )A、 B、 C、2 D、﹣22. 2019新型冠状病毒的直径是0.00013mm,将0.00013用科学记数法表示是( )A、130×10﹣6 B、13×10﹣3 C、1.3×10﹣4 D、1.3×10﹣53. 下列图形中,不是中心对称图形的是( )A、
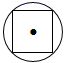 B、
B、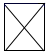 C、
C、 D、
D、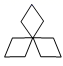 4. 下列计算正确的是( )A、8a﹣a=7 B、a2+a2=2a4 C、(2m)3=8m3 D、a6÷a2=a35. 为了了解学生线上学习情况,老师抽查某组10名学生的单元测试成绩如下:78,86,60,108,112,116,90,120,54,116这组数据的平均数和中位数分别为( )A、95,99 B、94,99 C、94,90 D、95,1086. 下列四个命题中,真命题有( )
4. 下列计算正确的是( )A、8a﹣a=7 B、a2+a2=2a4 C、(2m)3=8m3 D、a6÷a2=a35. 为了了解学生线上学习情况,老师抽查某组10名学生的单元测试成绩如下:78,86,60,108,112,116,90,120,54,116这组数据的平均数和中位数分别为( )A、95,99 B、94,99 C、94,90 D、95,1086. 下列四个命题中,真命题有( )①两条直线被第三条直线所截,同位角相等;②实数与数轴上的点是一一对应的;③三角形的一个外角大于任何一个内角;④平面内点 到 轴的距离是2.
A、1个 B、2个 C、3个 D、4个7. 若菱形的周长为16,高为2,则菱形两邻角的度数之比为( )A、4:1 B、5:1 C、6:1 D、7:18. 如图,在锐角 ABC中,小明进行了如下的尺规作图:①分别以点A、B为圆心,以大于 的长为半径作弧,两弧分别相交于点P、Q;
②作直线PQ分别交边AB、BC于点E、D;
③连接AD. 若AD=7,sin∠DAC= ,BC=9.
则AC的长为( )
 A、9 B、 C、 D、9. 在平面直角坐标系中,长为2的线段 (点D在点C右侧)在x轴上移动 , ,连接 、 ,则 的最小值为( )
A、9 B、 C、 D、9. 在平面直角坐标系中,长为2的线段 (点D在点C右侧)在x轴上移动 , ,连接 、 ,则 的最小值为( ) A、 B、 C、 D、10. 如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是( )
A、 B、 C、 D、10. 如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是( )
⑴EF= OE;
⑵S四边形OEBF:S正方形ABCD=1:4;
⑶BE+BF= OA;
⑷在旋转过程中,当△BEF与△COF的面积之和最大时,AE= ;
⑸OG•BD=AE2+CF2 .
A、(1)(2)(3)(5) B、(1)(3)(4)(5) C、(2)(3)(4)(5) D、(1)(2)(3)(4)二、填空题
-
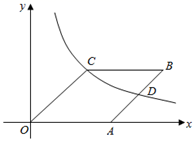
11. 因式分解:16a3b﹣ab= .12. 经过人民路十字路口红绿灯处的两辆汽车,可能直行,也可能左转,如果这两种可能性大小相同,则至少有一辆向左转的概率是.13. 定义运算: ,若 , 是方程 的两个根,则 的值为 .14. 如图,在平面直角坐标系中,已知菱形OABC,点A的坐标为(3,0),点B,C均在第一象限,反比例函数y= (x>0)的图象经过点C,且与边AB交于点D,若D是AB的中点,则k的值为 .
 15. 如图,在菱形ABCD中,∠A=60°,AB=3,点M为AB边上一点,AM=2,点N为AD边上的一动点,沿MN将△AMN翻折,点A落在点P处,当点P在菱形的对角线上时,AN的长度为 .
15. 如图,在菱形ABCD中,∠A=60°,AB=3,点M为AB边上一点,AM=2,点N为AD边上的一动点,沿MN将△AMN翻折,点A落在点P处,当点P在菱形的对角线上时,AN的长度为 .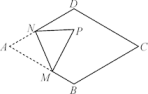
三、解答题
-
16.17. 先化简,再求值: ,其中 .18. 学生社团是指学生在自愿基础上结成的各种群众性文化、艺术、学术团体.不分年级、由兴趣爱好相近的同学组成,在保证学生完成学习任务和不影响学校正常教学秩序的前提下开展各种活动.某校就学生对“篮球社团、动漫社团、文学社团和摄影社团”四个社团选择意向进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整).
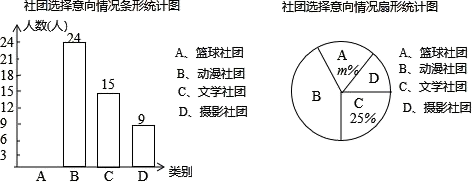
请根据图中信息,解答下列问题:
(1)、求扇形统计图中m的值,并补全条形统计图;(2)、在“动漫社团”活动中,甲、乙、丙、丁、戊五名同学表现优秀,现决定从这五名同学中任选两名参加“中学生原创动漫大赛”,恰好选中甲、乙两位同学的概率为.(3)、已知该校有1200名学生,请估计“文学社团”共有多少人?19. 如图,矩形 中,点 在边 上,将 沿 折叠,点 落在 边上的点 处,过点 作 交 于点 ,连接 .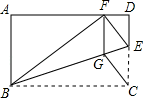 (1)、求证:四边形 是菱形;(2)、若 ,求四边形 的面积.20. 5月18日,我市九年级学生安全有序开学复课.为切实做好疫情防控工作,开学前夕,我市某校准备在民联药店购买口罩和水银体温计发放给每个学生.已知每盒口罩有100只,每盒水银体温计有10支,每盒口罩价格比每盒水银体温计价格多150元.用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同.(1)、求每盒口罩和每盒水银体温计的价格各是多少元?(2)、如果给每位学生发放2只口罩和1支水银体温计,且口罩和水银体温计均整盒购买.设购买口罩m盒(m为正整数),则购买水银体温计多少盒能和口罩刚好配套?请用含m的代数式表示.(3)、在民联药店累计购医用品超过1800元后,超出1800元的部分可享受8折优惠.该校按(2)中的配套方案购买,共支付w元,求w关于m的函数关系式.若该校九年级有900名学生,需要购买口罩和水银体温计各多少盒?所需总费用为多少元?21. 定义:有一组对角互余的四边形叫做对余四边形.(1)、理解:若四边形 是对余四边形,则 与 的度数之和为;(2)、证明:如图1, 是 的直径,点 在 上, , 相交于点D.
(1)、求证:四边形 是菱形;(2)、若 ,求四边形 的面积.20. 5月18日,我市九年级学生安全有序开学复课.为切实做好疫情防控工作,开学前夕,我市某校准备在民联药店购买口罩和水银体温计发放给每个学生.已知每盒口罩有100只,每盒水银体温计有10支,每盒口罩价格比每盒水银体温计价格多150元.用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同.(1)、求每盒口罩和每盒水银体温计的价格各是多少元?(2)、如果给每位学生发放2只口罩和1支水银体温计,且口罩和水银体温计均整盒购买.设购买口罩m盒(m为正整数),则购买水银体温计多少盒能和口罩刚好配套?请用含m的代数式表示.(3)、在民联药店累计购医用品超过1800元后,超出1800元的部分可享受8折优惠.该校按(2)中的配套方案购买,共支付w元,求w关于m的函数关系式.若该校九年级有900名学生,需要购买口罩和水银体温计各多少盒?所需总费用为多少元?21. 定义:有一组对角互余的四边形叫做对余四边形.(1)、理解:若四边形 是对余四边形,则 与 的度数之和为;(2)、证明:如图1, 是 的直径,点 在 上, , 相交于点D.求证:四边形 是对余四边形;
 (3)、探究:如图2,在对余四边形 中, , ,探究线段 , 和 之间有怎样的数量关系?写出猜想,并说明理由.
(3)、探究:如图2,在对余四边形 中, , ,探究线段 , 和 之间有怎样的数量关系?写出猜想,并说明理由. 22. 在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2ax+ 与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为C,直线AC交y轴于点D,D为AC的中点.
22. 在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2ax+ 与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为C,直线AC交y轴于点D,D为AC的中点. (1)、如图1,求抛物线的解析式;(2)、如图2,点P为抛物线对称轴右侧上的一动点,过点P作PQ⊥AC于点Q,设点P的横坐标为t,点Q的横坐标为m,求m与t的函数关系式;(3)、在(2)的条件下,如图3,连接AP,过点C作CE⊥AP于点E,连接BE、CE分别交PQ于F、G两点,当点F是PG中点时,求点P的坐标.
(1)、如图1,求抛物线的解析式;(2)、如图2,点P为抛物线对称轴右侧上的一动点,过点P作PQ⊥AC于点Q,设点P的横坐标为t,点Q的横坐标为m,求m与t的函数关系式;(3)、在(2)的条件下,如图3,连接AP,过点C作CE⊥AP于点E,连接BE、CE分别交PQ于F、G两点,当点F是PG中点时,求点P的坐标.