四川省内江市2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-08-17 类型:期末考试
一、单选题
-
1. 下列各式中,是分式的是( )A、 B、 C、 D、2. 成人每天维生素D的摄入量约为0.00000046克,将数据0.00000046用科学记数法表示为( )A、 B、 C、 D、3. 点M位于平面直角坐标系第四象限,且到x轴的距离是5,到y轴的距离是2,则点M的坐标是( )A、(2,﹣5) B、(﹣2,5) C、(5,﹣2) D、(﹣5,2)4. 下列不能判定四边形ABCD是平行四边形的条件是( )A、AB∥CD,AD∥BC B、OA=OC,OB=OD C、AB∥CD,AD=BC D、AB=CD,AD=BC5. 有15名学生参加学校举办的“最强大脑”智力竞赛,比赛结束后根据每个学生的成绩计算平均数、中位数、众数、方差,若去掉一个最高分,一个最低分,则一定不会发生变化的是( )A、平均数 B、中位数 C、众数 D、方差6. 下列说法正确的是( )A、对角线相等的四边形是矩形 B、对角线互相垂直且相等的四边形是正方形 C、对角线互相垂直平分的四边形是菱形 D、四边相等的四边形是正方形7. 如图,在矩形ABED中,AB=4,BE=EC=2,动点P从点E出发沿路径ED→DA→AB以每秒1个单位长度的速度向终点B运动;设点P的运动时间为t秒,△PBC的面积为S,则下列能反映S与t的函数关系的图象是( )
 A、
A、 B、
B、 C、
C、 D、
D、 8. 在同一直角坐标系中,函数 与 的图象可能是( )A、
8. 在同一直角坐标系中,函数 与 的图象可能是( )A、 B、
B、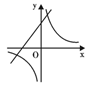 C、
C、 D、
D、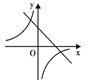 9. 如图,在正方形 中,等边三角形 的顶点 , 分别在边 和 上,则 ( )
9. 如图,在正方形 中,等边三角形 的顶点 , 分别在边 和 上,则 ( ) A、60° B、65° C、75° D、80°10. 若关于x的方程 + =3的解为正数,则m的取值范围是( )
A、60° B、65° C、75° D、80°10. 若关于x的方程 + =3的解为正数,则m的取值范围是( )
A、m< B、m< 且m≠ C、m>﹣ D、m>﹣ 且m≠﹣11. 如图,将矩形纸片 放入直角坐标系中,边 在 轴上且过原点,连接 .将纸片沿 折叠,使点 恰好落在边 上点 处,若 , ,则 的坐标为( )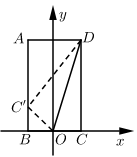 A、 B、 C、 D、12. 如图,直线 与直线 相交于点 ,直线 与 轴交于点 ,一动点 从点 出发,先沿平行于 轴的方向运动,到达直线 上的点 处后,改为垂直于 轴的方向运动,到达直线 上的点 处后,再沿平行于 轴的方向运动,到达直线 上的点 处后,又改为垂直于 轴的方向运动,到达直线 上的点 处后,仍沿平行于 轴的方向运动……照此规律运动,动点 依次经过点 , , , , , , 则 的长度为( )
A、 B、 C、 D、12. 如图,直线 与直线 相交于点 ,直线 与 轴交于点 ,一动点 从点 出发,先沿平行于 轴的方向运动,到达直线 上的点 处后,改为垂直于 轴的方向运动,到达直线 上的点 处后,再沿平行于 轴的方向运动,到达直线 上的点 处后,又改为垂直于 轴的方向运动,到达直线 上的点 处后,仍沿平行于 轴的方向运动……照此规律运动,动点 依次经过点 , , , , , , 则 的长度为( ) A、 B、 C、2020 D、4040
A、 B、 C、2020 D、4040二、填空题
-
13. 计算: .14. 若 ,则 .15. 如图,点 , 是反比例函数 图象上的两点,过点 、 分别作 轴于点 , 轴于点 ,连接OA, .已知点 , , ,则 .
 16. 如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=4,BO=DO=3,点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M,作PN⊥DC于点N. 连接PB,在点P运动过程中,PM+PN+PB的最小值等于 .
16. 如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=4,BO=DO=3,点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M,作PN⊥DC于点N. 连接PB,在点P运动过程中,PM+PN+PB的最小值等于 .
三、解答题
-
17.(1)、化简: .(2)、先化简 ,再从 ,0,1中选择合适的 值代入求值.18. 如图,在 中,点 , 分别是 , 上的点,且 ,分别过点 , 作 , ,垂足分别为 , ,连接 , .求证:四边形 是平行四边形.
 19. 某中学举办“信息技术知识答题竞赛”,八、九年级根据初赛成绩各选出5名选手组成代表队参加学校决赛,现将两个队各选出的5名选手的决赛成绩绘制成如下统计图表.
19. 某中学举办“信息技术知识答题竞赛”,八、九年级根据初赛成绩各选出5名选手组成代表队参加学校决赛,现将两个队各选出的5名选手的决赛成绩绘制成如下统计图表.八,九年级决赛成绩的条形统计图

平均分(分)
中位数(分)
众数(分)
方差(分 )
八年级
85
85
70
九年级
80
(1)、根据图表信息填空: , , ;(2)、计算九年级代表队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.20. 为迎接“五一”国际劳动节,某商场计划购进甲、乙两种品牌的 恤衫共100件,已知乙品牌每件的进价比甲品牌每件的进价贵30元,且用120元购买甲品牌的件数恰好是购买乙品牌件数的2倍.(1)、求甲、乙两种品牌每件的进价分别是多少元?(2)、商场决定甲品牌以每件50元出售,乙品牌以每件100元出售.为满足市场需求,购进甲种品牌的数量不少于乙种品牌数量的4倍,请你确定获利最大的进货方案,并求出最大利润.


