江苏省盐城市2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个图案中，是中心对称图形的为（）

A、 B、 C、 D、

查看试题解析
2. 下列事件中，属于必然事件的是（）

A、打开电视，正在播广告 B、分式方程有增根 C、没有水分，种子发芽 D、矩形的对角线相等

查看试题解析
3. 下列二次根式中，属于最简二次根式的是（）

A、 $\sqrt{8}$ B、 $\frac{1}{\sqrt{2}}$ C、 $\sqrt{2}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
4. 将分式 $\frac{2 x}{x + y}$ 中x、y的值都变为原来的2倍，则该分式的值（）

A、不变 B、变为原来的2倍 C、变为原来的4倍 D、变为原来的一半

查看试题解析
5. 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中，给出了著名的秦九韶公式，也叫三斜求积公式，即如果一个三角形的三边长分别为a，b，c，则该三角形的面积为S= $\sqrt{\frac{1}{4} [a^{2} b^{2} - {(\frac{a^{2} + b^{2} - c^{2}}{2})}^{2}]}$ ．现已知△ABC的三边长分别为1，2， $\sqrt{5}$ ，则△ABC的面积为（）

A、1 B、2 C、3 D、4

查看试题解析
6. 5G网络引领时代发展.5G网络峰值速率为4G网络峰值速率的10倍，在峰值速率下传输100兆数据，5G网络比4G网络快9秒，求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输x兆数据，根据题意，可列方程为（）

A、 $\frac{100}{10 x} - \frac{100}{x} = 9$ B、 $\frac{100}{x} - \frac{100}{10 x} = 9$ C、 $\frac{100 \times 10}{x} - \frac{100}{x} = 9$ D、 $\frac{100}{x} - \frac{100 \times 10}{x} = 9$

查看试题解析
7. 在平面直角坐标系中，点A的坐标为（2，3），将点 $A$ 绕原点逆时针旋转90°得到点 $A^{'}$ ，则点 $A^{'}$ 的坐标为（）

A、（－3，2） B、（3，－2） C、（3，2） D、（－2，－3）

查看试题解析
8. 关于x的分式方程 $\frac{1}{x - 2} + \frac{a - 2}{2 - x} =$ 1有增根，则a的值为（）

A、－1 B、5 C、1 D、3

查看试题解析

二、填空题

9. 若二次根式 $\sqrt{x - 3}$ 有意义，则实数x的取值范围是.

查看试题解析
10. 比较大小： $3 \sqrt{2}$ $2 \sqrt{3}$ （填“＞”或“＜”＝）.

查看试题解析
11. 从一批洗衣机中抽取10台，调查这批洗衣机的使用寿命，在这一抽样调查中，样本容量是.

查看试题解析
12. 计算： $\frac{a - c}{a - b} - \frac{c - b}{b - a}$ ＝.

查看试题解析

13. 某数学社团做摸球试验：一只不透明的袋子中装有若干个红球和白球，这些球除颜色外都相同.将这个袋中的球搅匀后从中任意摸出1个球，记下颜色后放回、搅匀，不断重复这个过程，获得如下数据：

摸球的个数n	200	300	400	500	1000	1600	2000
摸到白球的个数m	116	192	232	298	590	968	1202
摸到白球的频率 $\frac{m}{n}$	0.580	0.640	0.580	0.596	0.590	0.605	0.601

根据以上数据估计，摸到白球的概率约为（精确到0.01）.

查看试题解析

14. 如图，任意转动转盘1次，当转盘停止运动时，有下列事件：①指针落在标有数字7的区域内；②指针落在标有偶数数字的区域内；③指针落在标有3的倍数数字的区域内.请将这些事件的序号按事件发生的可能性从小到大的顺序依次排列为 .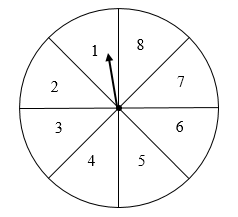

查看试题解析
15. 三个形状、大小相同的菱形按如图的方式摆放，已知△ABC为正三角形，若菱形的两条对角线长分别为3cm和 $3 \sqrt{3}$ cm，则△ABC的面积为 $c m^{2}$ .

查看试题解析
16. 如图，平行四边形ABCO的对角线AC、OB交于点D，反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象经过A、D两点，若平行四边形ABCO的面积是12，则k＝.

查看试题解析

三、解答题

17. 计算： $\sqrt{6} \times (2 \sqrt{12} - 3 \sqrt{\frac{1}{3}})$ .

查看试题解析
18. 解方程： $\frac{3 x + 2}{x - 1} = \frac{5}{x - 1}$

查看试题解析
19. 先化简，再求值： $(\frac{x^{2} + 4}{x} - 4) \div \frac{x^{2} - 4}{x^{2} + 2 x}$ ，其中 $x = - 1$ .

查看试题解析
20. 某校组织八年级学生参加“A.航模、B.湿地文化、C.羽翼合唱、D.红色讲解”4个社团，要求每人必须参加，并且每人只能选择其中的一个社团.为了解学生对这几个社团的选择意向，学校从全体学生中随机抽取部分学生进行问卷调查，并把调查结果制成如图所示的扇形统计图和条形统计图（部分信息未给出）.请你根据给出的信息解答下列问题：

(1)、求参加这次问卷调查的学生人数，并补全条形统计图（画图后请标注相应的数据）；

(2)、m＝， n＝；

(3)、若该校八年级共有1800名学生，试估计该校选择意向为“红色讲解”社团的学生有多少人？

查看试题解析
21. 平行四边形的一个判定定理是：对角线互相平分的四边形是平行四边形.请你证明这个判定定理.
已知：如图，在四边形ABCD中，AC，BD相交于点O，OA＝OC，OB＝OD.

求证：四边形ABCD是平行四边形.

证明：

查看试题解析
22. 如图，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象交于点A（1，3）、B（n，－1）.

(1)、求这两个函数的表达式；

(2)、已知P（a，0），其中a＞0，过点P作与y轴平行的直线，分别交一次函数 $y = k x + b$ 的图象和反比例函数 $y = \frac{m}{x}$ 的图象于点M、N.若PM＞PN，结合函数图象直接写出a的取值范围.

查看试题解析
23. 如图，E是正方形ABCD对角线BD上一点，且BE＝BC，EF⊥BD，交DC于点F.求证：DE＝CF.

查看试题解析
24. 为防控新冠疫情，某校对教室采取喷洒药物的方式进行消毒.在消毒过程中，先进行5min的药物喷洒，接着封闭教室10min，然后打开门窗进行通风.教室内每立方米空气中的含药量y（mg/m³）与药物在空气中的持续时间x（min）之间的函数关系如图所示，在打开门窗通风前分别满足两个一次函数关系，在通风后满足反比例函数关系.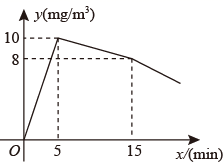

(1)、求药物喷洒后空气中含药量y（mg/m³）与药物在空气中的持续时间x（min）之间的函数表达式；

(2)、如果室内空气中的含药量不低于5mg/m³且持续时间不低于20分钟，才能有效消毒，通过计算说明此次消毒是否有效？

查看试题解析
25. 如图，在四边形ABCD中，点E、F、G、H分别是边AB、BC、CD、DA的中点，连接EF、FG、GH、EH.

(1)、求证：四边形EFGH是平行四边形；

(2)、再加上条件 ▲ 后，能使得四边形EFGH是矩形.请从①四边形ABCD是菱形，②四边形ABCD是矩形这两个条件中选择1个条件填空（写序号），重新画图并写出证明过程.

查看试题解析
26. （发现问题）
小明在学习过程中发现：周长为定值的矩形中面积最大的是正方形.那么，面积为定值的矩形中，其周长的取值范围如何呢？

（解决问题）

小明尝试从函数图象的角度进行探究：

(1)、建立函数模型
设一矩形的面积为4，周长为m，相邻的两边长为x、y，则x $\cdot$ y＝4，2（x＋y）＝m，

即 $y = \frac{4}{x}$ ， $y = - x + \frac{m}{2}$ ，那么满足要求的（x，y）应该是函数 $y = \frac{4}{x}$ 与 $y = - x + \frac{m}{2}$ 的图象在第象限内的公共点坐标.

(2)、画出函数图象
①画函数 $y = \frac{4}{x}$ （x＞0）的图象；

②在同一直角坐标系中直接画出 $y = - x$ 的图象，则 $y = - x + \frac{m}{2}$ 的图象可以看成是由 $y = - x$ 的图象向右平移 ▲ 个单位长度得到.

(3)、研究函数图象：平移直线 $y = - x$ ，观察两函数的图象；
①当直线平移到与函数 $y = \frac{4}{x}$ （x＞0）的图象有唯一公共点的位置时，公共点的坐标为 ▲ ，周长m的值为 ▲ ；

②在直线平移的过程中，两函数图象公共点的个数还有什么情况？请直接写出公共点的个数及对应周长m的取值范围.

(4)、（结论运用）面积为10的矩形的周长m的取值范围为.

查看试题解析