江苏省无锡市锡山区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-08-17 类型:期末考试
一、单选题
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列二次根式中属于最简二次根式的是( )A、 B、 C、 D、3. 若点 在反比例函数的图象上,则 的值为( )A、-18 B、18 C、-2 D、24. “翻开华东师大版数学九年级上册,恰好翻到第50页”,这个事件是( )A、必然事件 B、随机事件 C、不可能事件 D、确定事件5. 下列性质中,菱形具有而矩形不一定具有的是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、邻边互相垂直6. 在同一平面直角坐标系中,函数y=mx+m与y= (m≠0)的图象可能是( )A、
2. 下列二次根式中属于最简二次根式的是( )A、 B、 C、 D、3. 若点 在反比例函数的图象上,则 的值为( )A、-18 B、18 C、-2 D、24. “翻开华东师大版数学九年级上册,恰好翻到第50页”,这个事件是( )A、必然事件 B、随机事件 C、不可能事件 D、确定事件5. 下列性质中,菱形具有而矩形不一定具有的是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、邻边互相垂直6. 在同一平面直角坐标系中,函数y=mx+m与y= (m≠0)的图象可能是( )A、 B、
B、 C、
C、 D、
D、 7. 化简二次根式的正确结果是( )A、 B、 C、 D、8. 已知 是反比例函数 的图象上三点,且 ,则下列结论正确的是( )A、 B、 C、 D、9. 如图,四边形 和四边形 都是正方形,反比例函数 在第一象限的图象经过点 ,若两正方形的面积差为12,则 的值为
7. 化简二次根式的正确结果是( )A、 B、 C、 D、8. 已知 是反比例函数 的图象上三点,且 ,则下列结论正确的是( )A、 B、 C、 D、9. 如图,四边形 和四边形 都是正方形,反比例函数 在第一象限的图象经过点 ,若两正方形的面积差为12,则 的值为 A、12 B、6 C、-12 D、810. 如图,在矩形 中, , , 是 的中点,将 沿直线 翻折,点落 在点 处,连结 ,则 的长为( )
A、12 B、6 C、-12 D、810. 如图,在矩形 中, , , 是 的中点,将 沿直线 翻折,点落 在点 处,连结 ,则 的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若式子 在实数范围内有意义,则x的取值范围是 .12. 当x=时,分式 的值为0.13. 一组数据共有 个,分成 组后其中前四组的频数分别是 ,则第 组数据的频率为.14. 如图,在正方形 中, 为对角线, 为 上一点,连接 , , 的延长线交 于点 , ,则 的度数为.
 15. 如图,从一个大正方形中裁去面积为8cm2和18cm2的两个小正方形,则留下的阴影部分面积和为 。
15. 如图,从一个大正方形中裁去面积为8cm2和18cm2的两个小正方形,则留下的阴影部分面积和为 。 16. 若实数 满足 ,则 .17. 如图,在四边形 中, , °, , ,点 分别为 上的动点(含端点), 分别为 的中点,则 长度的最小值为.
16. 若实数 满足 ,则 .17. 如图,在四边形 中, , °, , ,点 分别为 上的动点(含端点), 分别为 的中点,则 长度的最小值为. 18. 如图,在平面直角坐标系中有一个 的矩形 网格,每个小正方形的边长都是 个单位长度,反比例函数 的图象经过格点 (小正方形的顶点),同时还经过矩形 的边 上的 点,反比例函数 的图象经过格点 ,且 ,则 的值是.
18. 如图,在平面直角坐标系中有一个 的矩形 网格,每个小正方形的边长都是 个单位长度,反比例函数 的图象经过格点 (小正方形的顶点),同时还经过矩形 的边 上的 点,反比例函数 的图象经过格点 ,且 ,则 的值是.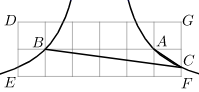
三、解答题
-
19. 计算:(1)、 ;(2)、 .20.(1)、化简: ;(2)、解方程: .21. 先化简,再求值: ,其中 .22. 如图1与图2,在边长均为1个单位长度的小正方形组成的网格中, 的顶点及点 均在格点上.请仅用无刻度直尺完成作图(保留作图痕迹).
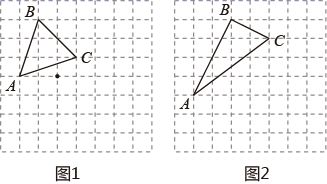 (1)、在图1中,作 关于点 成中心对称的 ;(2)、在图2中.
(1)、在图1中,作 关于点 成中心对称的 ;(2)、在图2中.①作 绕点 顺时针旋转一定角度后,顶点仍在格点上的 ;
②请直接写出:点 到 的距离为 ▲ .
23. 2020年3月,中共中央、国务院颁布了《关于全面加强新时代大中小学劳动教育的意见》.区教育局发布了“普通中小学劳动教育状况评价指标”,为了解某校学生一周劳动次数的情况,随机抽取若干学生进行调查,得到如下统计图: (1)、这次调查活动共抽取 人,“2次”所在扇形对应的圆心角的度数是 °;(2)、请将条形统计图补充完整;(3)、若该校学生共有3000人,根据调查结果,请你估计该校一周劳动“ 次及以下”的学生人数.24. 如图,在菱形ABCD中,对角线AC、BD相交于点O , 过点D作对角线BD的垂线交BA的延长线于点E.
(1)、这次调查活动共抽取 人,“2次”所在扇形对应的圆心角的度数是 °;(2)、请将条形统计图补充完整;(3)、若该校学生共有3000人,根据调查结果,请你估计该校一周劳动“ 次及以下”的学生人数.24. 如图,在菱形ABCD中,对角线AC、BD相交于点O , 过点D作对角线BD的垂线交BA的延长线于点E. (1)、证明:四边形ACDE是平行四边形;(2)、若AC=8,BD=6,求平行四边形ACDE的面积.25. 某店经营的 款手机去年销售总额为60000元,今年每部销售价比去年降低500元,若卖出的数量相同,则销售总额将比去年减少25%.已知 两款手机的进货和销售价格如下表:
(1)、证明:四边形ACDE是平行四边形;(2)、若AC=8,BD=6,求平行四边形ACDE的面积.25. 某店经营的 款手机去年销售总额为60000元,今年每部销售价比去年降低500元,若卖出的数量相同,则销售总额将比去年减少25%.已知 两款手机的进货和销售价格如下表:款手机
款手机
进货价格(元)
1100
1400
销售价格(元)
今年的销售价格
2000
(1)、今年 款手机每部售价多少元?(2)、该店计划新进一批 款手机和 款手机共60部,且 款手机的进货数量不超过 款手机数量的3倍,应如何进货才能使这批手机获利最多?


