江苏省无锡市梁溪区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列统计图表中，能够直观地反映各部分占总体的百分比的是（）

A、条形统计图 B、扇形统计图 C、折线统计图 D、频率分布直方图

查看试题解析
2. 某随机事件 $A$ 发生的概率 $P (A)$ 的值不可能是（）

A、0.0001 B、0.5 C、0.99 D、1

查看试题解析
3. 当 $x \geq 2$ 时，下列式子一定有意义的是（）

A、 $\frac{1}{x - 2}$ B、 $\frac{1}{x - 3}$ C、 $\sqrt{x - 1}$ D、 $\sqrt{x - 3}$

查看试题解析
4. 下列二次根式不是最简二次根式的是（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\sqrt{6}$ D、 $\sqrt{8}$

查看试题解析
5. 如果把分式 $\frac{x y}{x + y}$ 中的 $x$ 和 $y$ 都扩大3倍，那么分式的值（）

A、不变 B、扩大3倍 C、扩大6倍 D、扩大9倍

查看试题解析
6. 分式 $\frac{1}{2 a^{2} b}$ 与 $\frac{1}{6 a b^{2} c}$ 的最简公分母是（）

A、 $a b c$ B、 $a^{2} b^{2} c$ C、 $6 a^{2} b^{2} c$ D、 $12 a^{2} b^{2} c$

查看试题解析
7. 下列图形中是中心对称图形的是（）

A、三角形 B、四边形 C、平行四边形 D、梯形

查看试题解析
8. 矩形具有而菱形不具有的性质是（）

A、对边相等 B、邻边垂直 C、对角线互相平分 D、对角线互相垂直

查看试题解析
9. 如果一个反比例函数的图象经过点 $(3 ， 2)$ ，那么下列各点中在此函数图象上的点是（）

A、 $(- 3 ， - 2)$ B、 $(- 1 ， - 5)$ C、 $(2 ， - 3)$ D、 $(5 ， 1)$

查看试题解析
10. 对于 $\sqrt{11 - 6 \sqrt{2}}$ 这样的根式，我们可以利用“配方法”进行化简： $\sqrt{11 - 6 \sqrt{2}} = \sqrt{9 - 2 \sqrt{18} + 2}$ $= \sqrt{{(\sqrt{9} - \sqrt{2})}^{2}} = 3 - \sqrt{2}$ .运用同样的方法化简 $\sqrt{23 - 6 \sqrt{10 + 4 \sqrt{3 - 2 \sqrt{2}}}}$ 的结果是（）

A、 $3 - \sqrt{3}$ B、 $3 - \sqrt{2}$ C、 $5 - \sqrt{3}$ D、 $5 - \sqrt{2}$

查看试题解析

二、填空题

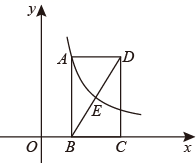
11. 不改变分式的值，使分式的分子与分母的最高次项的系数是正数： $\frac{3 x}{1 - x^{2}} =$ .

查看试题解析
12. 为了解我区八年级 $5200$ 名学生的身高情况，抽查了其中 $400$ 名学生的身高情况.在这个抽样调查中，样本容量是.

查看试题解析
13. 在一个不透明的袋子中装有2个红球、5个白球和3个黑球，这些球除颜色外都相同.从中任意摸出1个球，摸到色的球的可能性最大.(填“红”、“白”或“黑”)

查看试题解析
14. $Δ A B C$ 中， $M 、 N$ 分别为 $A B 、 A C$ 的中点，若 $M N = 3 ，$ 则 $B C =$

查看试题解析
15. 如果菱形的两条对角线长为 $10 c m$ 与 $12 c m$ ，则此菱形的面积 $c m^{2}$

查看试题解析
16. 已知 $a > b ，$ 且 $a^{2} + b^{2} = 3 a b$ ，则 $\frac{a + b}{a - b}$ 的值是.

查看试题解析
17. 已知点 $A (2 ， a) 、 B (b ， - 3)$ 都在函数的图象 $y = \frac{- 12}{x}$ 上，若将这个函数图象向左平行3个单位长度，则曲线 $A B$ 所扫过的图形的面积是.

查看试题解析
18. 如图，矩形 $A B C D$ 的边 $B C$ 在 $x$ 轴上，点 $E$ 是对角线 $B D$ 的中点，函数 $y = \frac{2}{x}$ 的图象经过 $A 、 E$ 两点，若 $∠ A B D = 45^{\circ}$ ，则直线 $B D$ 所对应的函数表达式是.

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{12} - \sqrt{18} + \sqrt{\frac{1}{2}}$

(2)、 $(3 + \sqrt{10}) (\sqrt{2} - \sqrt{5})$

查看试题解析
20.

(1)、计算： $\frac{2 x}{x^{2} - 9} - \frac{1}{x - 3}$

(2)、解方程： $\frac{1}{x - 2} = \frac{1 - x}{2 - x} - 3$

查看试题解析
21.

(1)、计算： $\frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \frac{1}{4 \times 5} + \cdot \cdot \cdot + \frac{1}{9 \times 10}$

(2)、设 $n$ 为正整数，求证： $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \dots + \frac{1}{(2 n - 1) (2 n + 1)} < \frac{1}{2}$

查看试题解析
22. 如图， $D ， E ， F$ 分别是 $△ A B C$ 各边的中点.

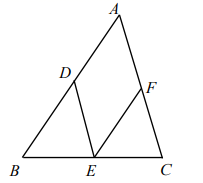(1)、四边形 $A D E F$ 是怎样的四边形？证明你的结论.

(2)、若 $∠ A = 90^{\circ}$ ，且 $A B = A C$ ，判断四边形 $A D E F$ 是怎样的四边形？证明你的结论.

查看试题解析

23. 我市6月16日至6月22日的气温情况如下：

日期	16日	17日	18日	19日	20日	21日	22日
最高气温 $(^{\circ} C)$	29	27	28	27	29	29	30
最低气温 $(^{\circ} C)$	23	24	22	21	20	20	20

(1)、用一个折线统计图描述这两组数据.

(2)、在这七天中，温差最大的是哪一天？最大温差是多少

^{\circ} C

？

查看试题解析

24. 如图，已知 $△ A B C$ 及点O，请用圆规和没有刻度的直尺完成下列作图：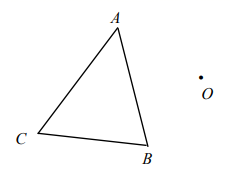

（ 1 ）作平行四边形 $A B C D$ ；

（ 2 ）作出 $△ A B C$ 关于点 $О$ 对称的 $△ A' B' C'$ .

查看试题解析
25. 某运输公司承担某项工程的运送土石方任务.已知需要运送的土石方总量为 $4 \times 10^{4}$ 立方米，设运输公司每天运送的土石方为 $V$ (立方米/天)，完成任务所需要的时间为 $t$ （天).

(1)、 $V$ 与 $t$ 之间有怎样的函数关系？

(2)、运输公司共派出20辆卡车，每辆卡车每天可运送土石方100立方米，工程进行了8天后，如果需要提前4天才能完成任务，那么该运输公司至少需要增派多少辆同样的卡车才能按时完成任务？

查看试题解析
26. 如图，已知正方形 $A B C D ，$ 点 $E$ 在 $C D$ 边上，以 $D E$ 为边在 $C D$ 左侧作正方形 $D E F G$ ；以 $D E ， D A$ 为邻边作平行四边形 $A D E H$ 连接 $C G ， D H$ .

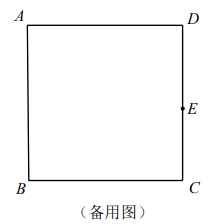(1)、判断 $C G$ 和 $D H$ 的数量及位置关系，并说明理由；

(2)、将 $D E$ 绕点 $D$ 顺时针旋转 $α^{\circ} (0 < α < 90)$ ，在旋转过程中， $C G$ 和 $D H$ 的数量及位置关系是否发生变化？请说明理由.

查看试题解析