江苏省泰州市姜堰区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-08-17 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列调查中,适宜采用全面调查方式的是( )A、调查一批新型节能灯泡的使用寿命 B、调查一批进口灌装饮料的防腐剂情况 C、对某市初中生每天阅读时间的调查 D、对某班学生视力情况的调查3. 下列事件中,是不可能事件的是( )A、打开电视,正在播放广告 B、没有水分,种子发芽 C、三天内将下雨 D、抛掷一枚质地均匀的硬币一次,出现正面朝上4. 下列等式成立的是( )A、 B、 C、 D、5. 近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知200度近视眼镜镜片的焦距为0.5m,则y与x的函数关系式为( )A、y= B、y= C、y= D、y=6. 如图,两个正方形的边长都为6,其中正方形 绕着正方形 的对角线的交点 旋转,正方形 与边 、 分别交于点 、 (不与端点重合),设两个正方形重叠部分形成图形的面积为 , 的周长为 ,则下列说法正确的是( )
2. 下列调查中,适宜采用全面调查方式的是( )A、调查一批新型节能灯泡的使用寿命 B、调查一批进口灌装饮料的防腐剂情况 C、对某市初中生每天阅读时间的调查 D、对某班学生视力情况的调查3. 下列事件中,是不可能事件的是( )A、打开电视,正在播放广告 B、没有水分,种子发芽 C、三天内将下雨 D、抛掷一枚质地均匀的硬币一次,出现正面朝上4. 下列等式成立的是( )A、 B、 C、 D、5. 近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知200度近视眼镜镜片的焦距为0.5m,则y与x的函数关系式为( )A、y= B、y= C、y= D、y=6. 如图,两个正方形的边长都为6,其中正方形 绕着正方形 的对角线的交点 旋转,正方形 与边 、 分别交于点 、 (不与端点重合),设两个正方形重叠部分形成图形的面积为 , 的周长为 ,则下列说法正确的是( )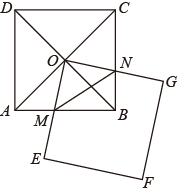 A、 发生变化, 存在最大值 B、 发生变化, 存在最小值 C、 不发生变化, 存在最大值 D、 不发生变化, 存在最小值
A、 发生变化, 存在最大值 B、 发生变化, 存在最小值 C、 不发生变化, 存在最大值 D、 不发生变化, 存在最小值二、填空题
-
7. 代数式 在实数范围内有意义,则x的取值范围是 .8. 计算:= .9. 化简:10. 设 、 是方程 的两个实数根,则 .11. 关于x的反比例函数 的图象位于第二、四象限,则m的取值范围是.12. 为解决群众看病贵的问题,某区有关部门决定降低药价,对某种原价为280元的药品进行连续两次降价,降价后的价格为240元,设平均每次降价的百分率为 ,由题意可列方程.13. 在一个不透明的袋子中装有2个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出白球的频率稳定在0.25附近,则估计袋子中的红球有个.14. 若 、 满足 ,则 .15. 如图,点 、 分别在反比例函数 和 图象上,分别过 、 两点向 轴、 轴作垂线,形成的阴影部分的面积为6,则 .
 16. 如图,点 为正方形 边 上一动点, , ,将点 绕点 顺时针旋转 到点 ,若 、 分别为 、 中点,则 的最小值为.
16. 如图,点 为正方形 边 上一动点, , ,将点 绕点 顺时针旋转 到点 ,若 、 分别为 、 中点,则 的最小值为.
三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 解下列方程:(1)、 ;(2)、 .19. 先化简,再求值: ,其中 .20. 为有效控制新型冠状病毒的传染,目前,国家正全面推开新冠疫苗的免费接种工作.某社区为了解其辖区内居民的接种情况,随机抽查了一部分居民进行问卷调查,把调查的结果分为 (已经接种)、 (准备接种)、 (观望中)、 (不接种)四种类别,并绘制了下面两幅不完整的统计图,请根据图中提供的信息解答下列问题:
 (1)、此次抽查的居民人数为人;(2)、请补全条形统计图,同时求出 类别所在扇形的圆心角度数;(3)、若该社区共有居民4000人,请你估计该社区已接种新冠疫苗的居民约有多少人?21. 已知关于 的方程 .(1)、求证:该方程有两个不相等的实数根;(2)、若该方程有一个根-1,求 的值.22. 在“慈善一日捐”活动中,甲、乙两校教师各捐款30000元,若乙校教师比甲校教师人均多捐20元,给出如下三个信息:
(1)、此次抽查的居民人数为人;(2)、请补全条形统计图,同时求出 类别所在扇形的圆心角度数;(3)、若该社区共有居民4000人,请你估计该社区已接种新冠疫苗的居民约有多少人?21. 已知关于 的方程 .(1)、求证:该方程有两个不相等的实数根;(2)、若该方程有一个根-1,求 的值.22. 在“慈善一日捐”活动中,甲、乙两校教师各捐款30000元,若乙校教师比甲校教师人均多捐20元,给出如下三个信息:①甲校教师的人数比乙校的教师人数多 ;
②甲、乙两校教师人数之比为 ;
③乙校比甲校教师人均捐款多 .
请从以上三个信息中选择一个作为条件,求甲、乙两校教师的人数各有多少人?
你选择的条件是 ▲ (填序号),并根据你选择的条件给出求解过程.
23. 如图,在矩形 中( ). (1)、仅用直尺和圆规在矩形 的边 上找一点 ,使 平分 .(不写作法,但要求保留作图痕迹)(2)、在(1)的条件下, , ,求 的长.24. 小明在学习二次根式时,碰到这样一道题,他尝试着运用分类讨论的方法解题如下:
(1)、仅用直尺和圆规在矩形 的边 上找一点 ,使 平分 .(不写作法,但要求保留作图痕迹)(2)、在(1)的条件下, , ,求 的长.24. 小明在学习二次根式时,碰到这样一道题,他尝试着运用分类讨论的方法解题如下:题目:若代数式 的值是1,求 的取值范围.
解:原式 ,
当 时,原式 ,解得 (舍去);
当 时,原式 ,符合条件;
当 时,原式 ,解得 (舍去);
所以, 的取值范围是 .
请你根据小明的做法,解答下列问题:
(1)、当 时,化简: ;(2)、若代数式 的值是4,求 的取值范围.25. 在正方形 中, , 、 分别是 、 边上的动点,以 、 为边作平行四边形 . (1)、如图1,连接 ,若 ,试说明 与 的关系;(2)、如图2,若 为 的中点, 在 边上是否存在某个位置,使得四边形 为菱形?若存在,求出 的长;若不存在,说明理由.(3)、设 ,若不论 在何位置, 与 始终不可能相等,求 的取值范围.26. 如图,直线 与反比例函数 交于点 ,与 轴交于点 ,连接 , .
(1)、如图1,连接 ,若 ,试说明 与 的关系;(2)、如图2,若 为 的中点, 在 边上是否存在某个位置,使得四边形 为菱形?若存在,求出 的长;若不存在,说明理由.(3)、设 ,若不论 在何位置, 与 始终不可能相等,求 的取值范围.26. 如图,直线 与反比例函数 交于点 ,与 轴交于点 ,连接 , .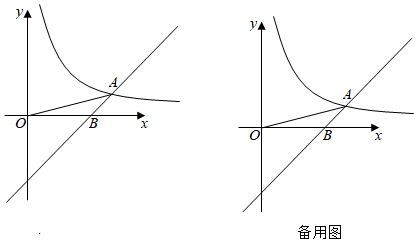 (1)、求点 的坐标及 的值;(2)、过 轴正半轴上一点 作 轴的垂线与直线 与反比例函数 的图象分别交于点 、 两点.
(1)、求点 的坐标及 的值;(2)、过 轴正半轴上一点 作 轴的垂线与直线 与反比例函数 的图象分别交于点 、 两点.①当 时,求 的长;
②若以 、 、 、 为顶点的四边形为平行四边形,求 的值;
(3)、直线 与直线 、反比例函数 的图象分别交于 、 ,若 ,直接写出 的取值范围.