江苏省苏州市苏州工业园区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中，与 $\sqrt{3}$ 是同类二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{8}$ C、 $\sqrt{12}$ D、 $\sqrt{24}$

查看试题解析
2. 当 $x = 1$ 时，下列分式没有意义的是（）

A、 $\frac{x + 1}{x}$ B、 $\frac{x}{x - 1}$ C、 $\frac{x - 1}{x}$ D、 $\frac{x}{x + 1}$

查看试题解析
3. 将两个全等的矩形按如图方式摆放，则该图形（）

A、既不是轴对称图形也不是中心对称图形 B、是中心对称图形但并不是轴对称图形 C、是轴对称图形但并不是中心对称图形 D、既是轴对称图形又是中心对称图形

查看试题解析
4. 下列整数中，与 $8 - \sqrt{15}$ 最接近的是（）

A、2 B、3 C、4 D、5

查看试题解析
5. “黄梅时节家家雨，青草池塘处处蛙.”如图，梅雨时节的苏州，粉墙黛瓦、小桥流水，宛如一幅水墨诗画.某天，气象台预报明天降雨的概率是90%，则以下判断正确的是（）

A、明天一定会下雨 B、明天有90%的地区会降雨 C、明天有90%的时间会下雨 D、明天下雨的可能性很大

查看试题解析
6. 下列调查中，适合采用普查的是（）

A、调查中央电视台《开学第一课》的收视率 B、调查气象卫星的零部件质量 C、调查某品牌新能源汽车的最大续航里程 D、调查某城市居民6月份人均网上购物的次数

查看试题解析
7. 反比例函数 $y = \frac{k}{x}$ （k为正整数）在第一象限的图象如图所示，已知图中点A的坐标为 $(2 ， 1)$ ，则k的值是（）

A、1 B、2 C、3 D、4

查看试题解析
8. 如图，在方格纸中，格点三角形甲经过旋转后得到格点三角形乙，则旋转中心是（）

A、格点A B、格点B C、格点C D、格点D

查看试题解析
9. 我国古代著作《四元玉鉴》记载“买橡多少”问题：“六贯二百一十钱，倩人去买几株椽，每株脚钱三文足，无钱准与一株椽.”，其大意为：现请人代买一批橡，这批橡的价钱为6210文.如果每株橡的运费是3文，那么少拿一株橡后，剩下的橡的运费恰好等于一株椽的价钱，试问6210文能买多少株橡，设这批橡的数量为x株，则符合题意的方程是（）

A、 $\frac{6210}{x - 1} = 3$ B、 $3 x - 1 = \frac{6210}{x}$ C、 $3 (x - 1) = \frac{6210}{x - 1}$ D、 $\frac{6210}{x} = 3$

查看试题解析
10. 如图，在 $▱ A B C D$ 中， $A B = 4$ ， $B C = 8$ ， $∠ B = 60 °$ .分别以点B、D为圆心，大于 $\frac{1}{2} B D$ 长为半径画弧，两弧相交于点M、N，直线MN分别与AD、BC相交于点E、F，则EF的长为（）

A、 $\frac{4}{5} \sqrt{21}$ B、4 C、 $\frac{3}{5} \sqrt{21}$ D、 $\sqrt{13}$

查看试题解析

二、填空题

11. 化简 $\sqrt{2 \frac{1}{4}}$ ＝．

查看试题解析
12. 若 $\sqrt{a^{2}} = {(\sqrt{a})}^{2}$ ，则 $a$ 应满足的条件是.

查看试题解析
13. 已知 $\frac{1}{m} - \frac{1}{n} = 3$ ，则 $\frac{m n}{m - n} =$ .

查看试题解析
14. 已知点 $P$ 在线段 $A B$ 上，且 $P A^{2} = A B \cdot P B$ .若 $A B = 5 cm$ ，则 $P A \approx$ cm.（精确到0.1cm）

查看试题解析
15. 在一个不透明的袋子中有1个红球，2个白球和若干个黑球.小明将袋子中的球摇匀后，从中任意摸出一个球，记下颜色后放回袋中并摇匀.在多次重复以上操作后，小明统计了摸到红球的频率，并绘制了如图所示的折线统计图，则袋子中一共有球个.

查看试题解析
16. 如图，在四边形 $A B C D$ 中， $A B = A D$ ， $B C = D C$ .若 $∠ B A D = 60 °$ ， $∠ B C D = 30 °$ ， $B C = 4 cm$ ，则对角线 $A C$ 的长为cm.

查看试题解析
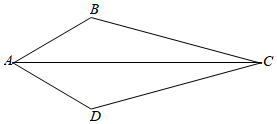17. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 3 cm$ ， $B C = 4 cm$ .将 $△ A B C$ 绕点 $C$ 按逆时针方向旋转后得 $△ D C E$ ，直线DA、BE相交于点F.取BC的中点G，连接GF，则GF长的最大值为cm.

查看试题解析
18. 如图，正方形瓷砖图案中的阴影部分是四个全等且顶角为45°的等腰三角形.已知该瓷砖的面积是 ${1m}^{2}$ ，则中间小正方形的面积为 $m^{2}$ .

查看试题解析

三、解答题

19. 计算 $\frac{\sqrt{6} - \sqrt{3}}{\sqrt{3}} + (2 + \sqrt{2}) (2 - \sqrt{2})$ .

查看试题解析
20. 解方程： $\frac{x + 3}{x - 3} - \frac{2}{x + 3} = 1$ .

查看试题解析
21. 先化简，再求值：（1﹣ $\frac{1}{a}$ ）÷ $\frac{a^{2} - 2 a + 1}{a}$ ，其中a＝ $\sqrt{2}$ +1

查看试题解析

22. 某区对4800名初中毕业生进行了一次视力抽样调查，根据调查结果，绘制如下了两幅不完整的统计图表.

初中毕业生视力抽样调查频数分布表

视力	频数（人）	频率
$4.0 \leq x < 4.3$	20	0.10
$4.3 \leq x < 4.6$	40	0.20
$4.6 \leq x < 4.9$	70	0.35
$4.9 \leq x < 5.2$		0.30
$5.2 \leq x < 5.5$	10

(1)、本次调查的样本容量为；

(2)、将频数分布表和频数分布直方图补充完整；

(3)、若视力在4.9以上（含4.9）均属标准视力，根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人？

查看试题解析

23. 某单位随机安排甲、乙两人到A、B、C三个社区进行新冠疫苗接种.

(1)、甲在A社区接种疫苗的概率是；

(2)、求甲、乙两人在同一个社区接种疫苗的概率.

查看试题解析
24. 如图，在 $▱ A B C D$ 中，点E是AD的中点，连接BE，BE、CD的延长线相交于点F，连接AF、BD.

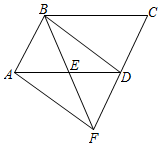(1)、求证：四边形ABDF是平行四边形；

(2)、当 $∠ C$ 与 $∠ B E D$ 满足条件时，四边形ABDF是矩形.

查看试题解析
25. 小明要把一篇文章录入电脑，完成录入的时间 $y$ （分）与录入文字的速度 $x$ （字/分）之间的函数关系如图.

(1)、求 $y$ 与 $x$ 之间的函数表达式；

(2)、小明在19：20开始录入，完成录入时不超过19：35，小明每分钟至少应录入多少个字？

(3)、小明为了收看19：30的新闻联播，将原定的录入速度提高了20%，结果比原计划提前2分钟完成，小明实际用了多少分钟完成文章的录入？

查看试题解析
26. 如图，安装路灯AB的路面CD比种植树木的地面PQ高 $1.2 m (C P = 1.2 m)$ 身高1.8m的小明MN站在距离C点15m远的路面上.在路灯的照射下，路基CP留在地面上的影长EP为0.4m，小明留在路面上的影长NF为3m，求路灯AB的高度.

查看试题解析
27. 如图

（理解概念）

一组邻边相等，且这组邻边所夹内角的对角被对角线平分的四边形叫做等平四边形，这条对角线叫做等平对角线.

(1)、下列四边形是等平四边形的是.（填序号）
①平行四边形；②菱形；③矩形；④正方形.

(2)、如图①，在等平四边形 $A B C D$ 中， $B C = D C$ ， $A C$ 平分 $∠ B A D$ .若 $A B > A D$ ，则 $∠ B$ 与 $∠ D$ 有怎样的数量关系？说明理由.

(3)、如图②，四边形 $A B C D$ 中， $B C = D C$ ， $∠ B A D = ∠ B C D = 90 °$ .求证：四边形 $A B C D$ 是等平四边形.

查看试题解析
28. 如图，在矩形 $A B C D$ 中， $A B = 5 cm$ ， $B C = 8 cm$ .点Р在边AD上，点A关于BP的对称点为E，连接AE、BE、DE.

(1)、当 $A E = B E$ 时， $A P =$ cm；

(2)、当 $D E // B P$ 时，求AP的长；

(3)、当 $△ A D E$ 为等腰三角形时，求AP的长.

查看试题解析