江苏省南京市联合体2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围（　　）

A、x≥2 B、x≤2 C、x＞2 D、x＜2

查看试题解析
3. 一只不透明的袋中装有除颜色外都相同的红球、黄球、白球共50个.通过多次摸球试验后，发现摸到红球、黄球的频率分别是0.3、0.5.则可估计袋中白球的个数是（）

A、10 B、15 C、20 D、25

查看试题解析
4. 已知反比例函数y＝ $\frac{k}{x}$ （k＜0）的图象经过点A（1，a）、B（3，b），则a与b的关系正确的是（）

A、a＜0＜b B、b＜a＜0 C、a＜b＜0 D、0＜a＜b

查看试题解析
5. 下列式子从左到右变形不正确的是（）

A、 $\frac{3 a}{3 b}$ ＝ $\frac{a}{b}$ B、 $\frac{- a}{b}$ ＝﹣ $\frac{a}{b}$ C、 $\frac{a^{2} + b^{2}}{a + b}$ ＝a+b D、 $\frac{a - 1}{1 - a}$ ＝﹣1

查看试题解析
6. 如图，在矩形ABCD中，E是AB的中点，动点F从点B出发，沿BC运动到点C时停止，以EF为边作▱EFGH，且点G、H分别在CD、AD上.在动点F运动的过程中，▱EFGH的面积（）

A、逐渐增大 B、逐渐减小 C、不变 D、先增大，再减小

查看试题解析

二、填空题

7. 计算：（ $\sqrt{3}$ ）²＝， $\sqrt{{(- 3)}^{2}}$ ＝.

查看试题解析
8. 若分式 $\frac{1}{x - 1}$ 在实数范围内有意义，则x的取值范围是.

查看试题解析
9. 给出下列3个分式： $\frac{2}{a b} ， \frac{1}{a^{2} b} ， \frac{3}{a b c}$ ，它们的最简公分母为.

查看试题解析
10. 如果反比例函数y= $\frac{k}{x}$ 的图象经过点（1，3），那么它一定经过点（﹣1，）．

查看试题解析
11. 为了解某市八年级学生每天的睡眠时间，从该市八年级学生中抽取1000名学生进行调查，该调查中的个体是 .

查看试题解析
12. 比较大小： $2 \sqrt{3}$ $3 \sqrt{2}$ （填“＞”、“＜”或“＝”）.

查看试题解析
13. 若关于x的分式方程 $\frac{3 x + 2}{x - 1}$ ＝ $\frac{m}{x - 1}$ 有增根，则实数m的值是 .

查看试题解析
14. 如图，在菱形ABCD中，∠BCD＝110°，AB的垂直平分线交对角线AC于点F，E为垂足，连接DF，则∠CDF等于°.

查看试题解析
15. 如图，在矩形ABCD中，P为矩形ABCD的边BC上任一点，PE⊥AC于点E，PF⊥BD于点F.若AB＝5，BC＝12，PE+PF＝

查看试题解析
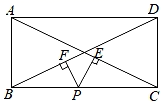16. 如图，Rt△ABC的边BC在x轴上，点D为斜边AB的中点，AC＝3，BC＝4，若反比例函数y＝ $\frac{k}{x}$ 的图象过点A、D，则k的值为 .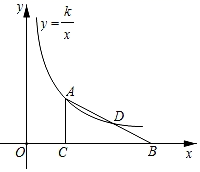

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{2 a^{3}} \cdot \sqrt{8 a} (a \geq 0)$ ；

(2)、 $\sqrt{6} \times (2 \sqrt{3} - 3 \sqrt{\frac{1}{3}})$

查看试题解析
18. 化简：

(1)、 $\frac{5 a + 3 b}{a^{2} - b^{2}}$ ﹣ $\frac{2 a}{a^{2} - b^{2}}$ ；

(2)、（1﹣ $\frac{1}{a - 1}$ ）÷（ $\frac{a^{2} - 4 a + 4}{a^{2} - a}$ ）.

查看试题解析
19. 先化简[ $\frac{3}{x - 1}$ ﹣ $\frac{3}{{(x - 1)}^{2}}$ ]÷ $\frac{x - 2}{x - 1}$ ，然后从﹣1，0，1，2中选取一个你认为合适的数作为x的值代入求值．

查看试题解析
20. 解方程： $\frac{1}{2 x - 4} + \frac{1}{2} = \frac{3}{2 - x}$ .

查看试题解析

21. 交警部门在全市范围开展了安全使用电瓶车专项宣传活动，在活动前和活动后分别随机抽取了部分使用电瓶车的市民，就骑电瓶车戴安全头盔情况进行问卷调查，将收集的数据制成统计图表.

活动前骑电瓶车戴安全帽情况统计表

类别	人数
A类（每次戴）	64
B类（经常戴）	245
C类（偶尔戴）	m
D类（都不戴）	170
合计	1000

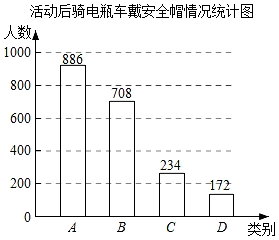(1)、“活动前骑电瓶车戴安全头盔情况统计表”中m的值为；

(2)、全市约有300万人使用电瓶车，请估计活动前全市骑电瓶车“都不戴”安全头盔的总人数；

(3)、小明认为，宣传活动后骑电瓶车“都不戴”安全头盔的人数为172，比活动前增加了2人，因此交警部门开展的宣传活动没有效果，小明的说法是否合理？为什么？

查看试题解析

22. 如图，点E、F分别在▱ABCD的边AB、CD的延长线上，且BE＝DF，连接AC、EF、AF、CE，AC与EF交于点O.

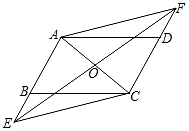(1)、求证：AC、EF互相平分；

(2)、若EF平分∠AEC，求证：四边形AECF是菱形.

查看试题解析
23. 为了改善生态环境，防止水土流失，某村计划在荒坡上种树1080棵.由于青年志愿者支援，实际每天种树的棵数比原计划每天多50%，结果提前6天完成任务.原计划每天种树多少棵？

查看试题解析
24. 如图，四边形ABCD为正方形，点E、F分别是AB、CD的中点，DG⊥CF于点G.

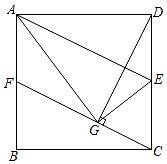(1)、求证：AE//CF；

(2)、求证：∠AGE＝90°；

(3)、若正方形的边长为2，则线段CG的长度为 .

查看试题解析
25. 如图，一次函数y₁＝mx+b与反比例函数y₂＝ $\frac{k}{x}$ 的图象交于A（1，2），B（﹣4， $- \frac{1}{2}$ ）两点.

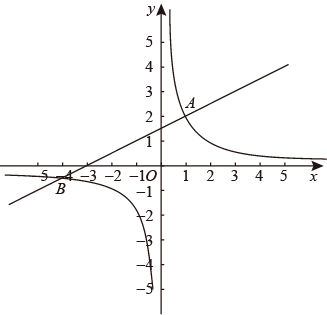(1)、分别求一次函数与反比例函数的关系式；

(2)、设函数 $y = y_{1} - y_{2}$ .
①当y＝0时，则x的值为 ▲ ；

②写出函数 $y = y_{1} - y_{2}$ 的增减性；

③在图中画y关于x的函数图象.

查看试题解析
26. 如图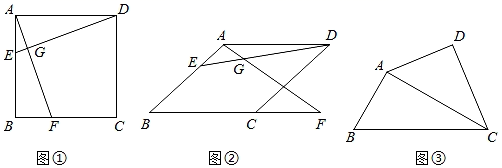

如图①，在正方形ABCD中，点E在AB上，点F在BC上，AF与DE相交于点G，AF＝DE，求证：∠DGF＝90°.

(1)、请完成上题的证明过程.

(2)、如图②，在菱形ABCD中，点E在AB上，点F在射线BC上，AF与DE相交于点G，AF＝DE，求证：∠DGF＝∠B.

(3)、如图③，已知四边形ABCD，利用直尺和圆规作线段EF，使点E、F分别在AB、CD上，且满足EF＝AC，EF与AC相交所形成的锐角等于∠B.

查看试题解析